【LeetCode】50. Pow(x, n)

leetcode

 

解题思路：快速幂算法（迭代法）

实现 pow(x, n) 的核心是高效计算幂函数。直接暴力循环（时间复杂度 O(n)）在指数较大时效率极低，因此采用​​快速幂算法​​（分治思想），将时间复杂度优化至 O(logn)。算法基于以下数学原理：

• ​​二进制分解​​：将指数 n 分解为二进制形式（例如 n=11 的二进制为 1011），则：

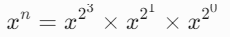
• ​​迭代计算​​：通过循环每次将指数右移（除以 2），同时底数平方（x←x²）。若当前二进制位为 1，则将当前底数乘入结果。

关键步骤

1. ​​处理边界情况​​：
   • 若 x=0，直接返回 0（题目要求 x≠0 或 n>0，但为鲁棒性考虑）。
   • 若 n=0，返回 1（任何数的 0 次幂为 1）。
2. ​​处理负指数​​：
   • 若 n<0，转换为计算 x⁻ⁿ=(1/x)ⁿ。为避免整数溢出（如 n=−2³¹ 时取负溢出），需将 n 转为 int64 类型。
3. ​​迭代计算​​：
   • 初始化结果 res = 1.0。
   • 循环直到指数为 0：
     • 若当前指数最低位为 1（n & 1 == 1），将当前底数乘入结果。
     • 底数平方（x *= x），指数右移一位（n >>= 1）。

复杂度分析

• ​​时间复杂度​​：O(logn)。每次循环指数减半，共 log_2​n 次迭代。
• ​​空间复杂度​​：O(1)。仅使用常数额外空间。

代码实现

func myPow(x float64, n int) float64 {
    // 边界: x为0时直接返回0
    if x == 0 {
        return 0
    }

    // 边界: n为0时返回1
    if n == 0 {
        return 1
    }

    // 处理负指数: 用int64避免溢出
    longN := int64(n)
    if longN < 0 {
        x = 1 / x
        longN = -longN
    }

    res := 1.0
    // 快速幂迭代
    for longN > 0 {
        if longN&1 == 1 { // 当前二进制为1
            res *= x
        }
        x *= x      // 底数平方
        longN >>= 1 // 指数右移
    }

    return res
} 

代码注释说明

1. ​​边界处理​​：
   • x == 0 时直接返回 0（避免除以 0 错误）。
   • n == 0 时返回 1（数学定义）。
2. ​​负指数转换​​：
   • 使用 int64 存储指数，避免 -n 溢出（如 n=−2³¹ 时）。
3. ​​迭代核心​​：
   • longN & 1 判断二进制最低位是否为 1。
   • x *= x 实现底数平方，对应指数减半。
   • longN >>= 1 等价于指数除以 2。

示例输出

func main() {
    // 输入：x = 2.00000, n = 10  输出：1024.00000
    fmt.Println(myPow(2.00000, 10))

    // 输入：x = 2.10000, n = 3  输出：9.26100
    fmt.Println(myPow(2.10000, 3))

    // 输入：x = 2.00000, n = -2  输出：0.25000
    // 解释：2-2 = 1/22 = 1/4 = 0.25
    fmt.Println(myPow(2.00000, -2))
}

1024
9.261
0.25
0 // (0.00001^2147483647 趋近于 0)

此实现高效处理大指数，并通过类型转换确保边界安全，符合题目要求。