支持向量机
背景知识
最优化问题一般是指对于某一个函数而言,求解在其指定作用域上的全局最小值
问题,一般分为以下三种情况(备注:除非函数是凸函数,否则以下方法求出来的解可能为局部最优解)
- 无约束问题:求解方式一般求解方式梯度下降法、牛顿法、坐标轴下降法等;
- 等式约束条件:求解方式一般为拉格朗日乘子法
- 不等式约束条件:求解方式一般为 KKT 条件
在优化问题中,根据目标函数存在形式分为 3 类:
- 线性规划:如果目标函数和约束条件都为变量 x 的线性函数,则称问题为线性规划;
- 二次规划:如果目标函数为二次函数,则称最优化问题为二次规划;
- 非线性优化:如果目标函数或者约束条件为非线性函数,则称最优化问题为非线性优化。
每个线性规划问题都有一个对应的对偶问题。对偶问题具有以下几个特性:
- 对偶问题的对偶是原问题;
- 无论原始问题是否是凸的,对偶问题都是凸优化问题;
- 对偶问题可以给出原始问题的一个下界;
- 当满足一定条件的时候,原始问题和对偶问题的解是完美等价的。
无约束问题-梯度下降法
推导过程见:线性模型之线性回归
等式约束问题-拉格朗日乘子法
目标函数:
- \(min \quad f(x,y)\)
- \(s.t. \quad g(x,y)=c\)
拉格朗日乘子法:
- \(L(x,y,\alpha)=f(x,y)+\alpha(g(x,y)-c) \quad \alpha \neq 0\)
求解:
- \(\nabla_{x,y,\alpha}L(x,y,\alpha)=0,\alpha \neq0\)
不等式约束问题-KKT条件
KTT 条件是泛拉格朗日乘子法的一种形式;是满足不等式约束情况下的条件。
目标函数:
- \(min \quad f(x,y)\)
- \(s.t. \quad h_k(x,y)=0, k=1,2,\cdots,p\)
- \(\quad \quad g_j(x)\leq0, j=1,2,\cdots,q\)
根据KKT条件:
- \(L(x,\alpha,\beta)=f(x)+\sum^p_{i=1}\alpha_ih_i(x)+\sum^q_{j=1}\beta_ig_i(x) \quad \alpha \neq 0,\beta\geq0\)
新目标函数:
- \(min_xL(x,\alpha,\beta)\)
推导KKT条件
目标函数为:
- \(min \quad f(x)\)
- \(s.t. \quad g(x)\leq0,j=1,2,\dots,q\)
\(\rightarrow\) \(L(x,\beta)=f(x)+\sum^q_{j=1}\beta_ig_i(x) \quad \beta\geq0\)
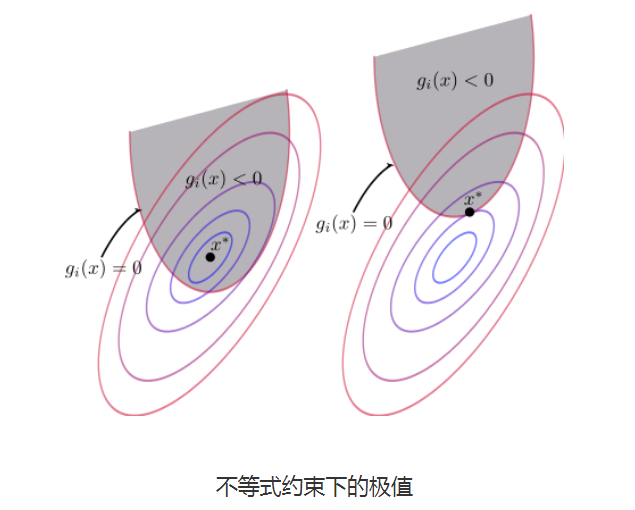
- 当极值点x在g(x)<0的区域中时,约束函数不起作用,直接\(\beta=0\),直接极小化f(x)即可
- 当极值点x在g(x)=0的区域内时,则变成等值约束(\(\beta g(x)=0\)),此时\(\beta\neq0\)
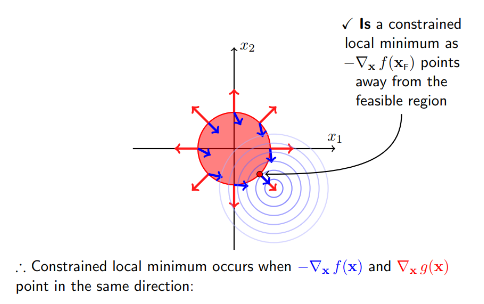
- 当极值点在约束函数\(g(x)\)外,此时可行解在约束边界上(\(\beta g(x)=0\)),这时可行解应尽量靠近无约束时的解,此时约束函数g(x)的梯度方向和目标函数f(x)的负梯度方向应相同,\(\beta>0,g(x)=0\)
- \(-\nabla_xf(x)=\beta\nabla_xg(x)\)
- 上式要求\(\beta>0\)
KKT条件总结:
- 拉格朗日取得最优解的充要条件;
\(\nabla_xL(x,\alpha,\beta)=0\) - 将不等式约束转换后的一个约束,称为松弛互补条件;
\(\beta_i g_i(x)=0,i=1,2,\cdots,q\) - 初始的约束条件
\(h_i(x)=0,i=1,2,\cdots,p\) - 初始的约束条件
\(g_i(x)\leq0,i=1,2,\cdots,q\) - 不等式约束需要满足的条件:
\(\beta_i\geq0,i=1,2,\cdots,q\)
KKT条件与对偶问题
KKT 条件是对偶问题的一个应用
目标函数为:
- \(min \quad f(x)\)
- \(s.t. \quad g(x)\leq0,j=1,2,\dots,q\)
\(\rightarrow\) \(L(x,\beta)=f(x)+\sum^q_{j=1}\beta_ig_i(x) \quad \beta\geq0\)
∵ \(\beta\neq0 \quad and \quad g_i(x)\leq0\)
∴\(\beta_ig_i(x)<0\)
∴\(f(x)=max_{\beta}L(x,\beta)\)
∴\(min_xf(x)=min_x max_{\beta}L(x,\beta)\)
此外:
∵ \(\beta\geq0 \quad and \quad g_i(x)\leq0 \rightarrow min_x\beta_ig_i(x)= 0 \quad or \quad -\infty\)
∴\(max_{\beta}min_x\beta_ig_i(x)= 0\)
∵\(max_{\beta}min_xL(x,\beta)=max_{\beta}[min_xf(x)+min_x\beta g(x)]=max_{\beta}min_xf(x) + max_{\beta}min_x\beta_ig_i(x)=max_{\beta}min_xf(x)=min_xf(x)\)
∴\(min_xf(x)=max_{\beta}min_xL(x,\beta); \beta=0或者g(x)=0\)
∴\(min_x max_{\beta}L(x,\beta)=max_{\beta}min_xL(x,\beta)\)即原问题=对偶问题
对偶问题的直观了解:最小的里面的那个最大的要比最大的那个里面的最小的大,从而就给原问题引入一个下界
如果存在\(x,\alpha,\beta\)满足上面KKT条件,那么他们就是原问题和对偶问题的可行解。
SVM
SVM:数据中找出一个分割超平面,让离超平面比较近的点尽可能的远离这个超平面
- 间隔(Margin):数据点到分割超平面的距离称为间隔。
- 支持向量(Support Vector):离分割超平面最近的那些点叫做支持向量。
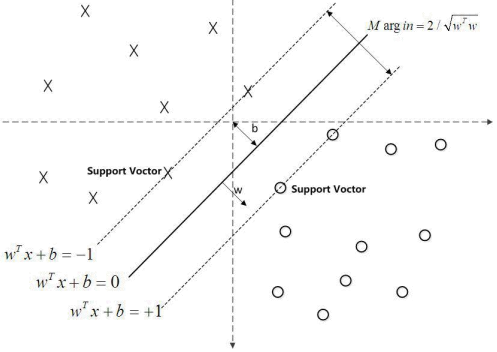
SVM 线性可分
支持向量到超平面的距离为:
∵ \(w^Tx+b=±1\)
∵ \(y\in\{+1,-1\}\)
∴ \(\frac{|y(w^Tx+b)|}{||w||_2}=\frac{2}{||w||_2}\)
之所以为2,主要是为了方便推导,可以理解为超平面两侧的支持向量的函数距离,对结果无影响。
优化问题为:
- \(max_{w,b}\frac{2}{||w||_2}\)
- \(s.t. \quad y^{(i)}(w^Tx^{(i)}+b)\geq1,i=1,2,\cdots,m\)
等价于:
- \(min_{w,b}\frac{1}{2}||w||_2^2\)
- \(s.t. \quad y^{(i)}(w^Tx^{(i)}+b)\geq1,i=1,2,\cdots,m\)
损失函数为:
- \(J(w)=\frac{1}{2}||w||_2^2\)
- \(s.t. \quad y^{(i)}(w^Tx^{(i)}+b)\geq1,i=1,2,\cdots,m\)
使用KKT条件转换为拉格朗日函数:
- \(L(w,b,\beta)=\frac{1}{2}||w||^2_2 +\sum_{i=1}^m\beta_i[1-y^{(i)}(w^Tx^{(i)}+b)],\beta \geq0\)
引入拉格朗日乘子后,优化目标变成:
- \(min_{w,b}max_{\beta\geq0}L(w,b,\beta)\)
根据拉格朗日对偶性特性,化为等价的对偶问题,则优化目标为:
- \(max_{\beta\geq0}min_{w,b}L(w,b,\beta)\)
使函数L极小化求w和b的取值:
- \(\frac{\partial L}{\partial w}=0\rightarrow w-\sum_{i=1}^m\beta_iy^{(i)}x^{(i)}=0\rightarrow w=\sum_{i=1}^m\beta_i y^{(i)}x^{(i)}\)
- \(\frac{\partial L}{\partial b}=0\rightarrow -\sum_{i=1}^m\beta_iy^{(i)}=0\rightarrow \sum_{i=1}^m\beta_i y^{(i)}=0\)
将w和b带入优化函数L中,优化函数为:
- \(l(\beta)=\frac{1}{2}||w||^2_2 +\sum_{i=1}^m\beta_i[1-y^{(i)}(w^Tx^{(i)}+b)]\)
- \(=\frac{1}{2}||w||^2_2 -\sum_{i=1}^m\beta_i[y^{(i)}(w^Tx^{(i)}+b)-1]\)
- \(=\frac{1}{2}w^Tw-\sum_{i=1}^m\beta_iy^{(i)}x^{(i)}-w^T\sum_{i=1}^m\beta_iy^{(i)}x^{(i)}-b\sum_{i=1}^m\beta_iy^{(i)}+\sum_{i=1}^m\beta_i\)
- \(=-\frac{1}{2}w^T\sum_{i=1}^m\beta_iy^{(i)}x^{(i)}-b\sum_{i=1}^m\beta_iy^{(i)}+\sum_{i=1}^m\beta_i\)
- \(=-\frac{1}{2}(\sum_{i=1}^m\beta_iy^{(i)}x^{(i)})^T(\sum_{i=1}^m\beta_iy^{(i)}x^{(i)})+\sum_{i=1}^m\beta_i\)
- \(=-\frac{1}{2}(\sum_{i=1}^m\beta_iy^{(i)}x^{(i)^T})(\sum_{i=1}^m\beta_iy^{(i)}x^{(i)})+\sum_{i=1}^m\beta_i\)
- \(=\sum_{i=1}^m\beta_i-\frac{1}{2}(\sum_{i=1}^m\sum_{j=1}^m\beta_i\beta_jy^{(i)}y^{(j)}x^{(i)^T}x^{(j)}\)
\(max l(\beta)\rightarrow min-l(\beta),\)优化函数为:
- \(min\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\beta_i\beta_jy^{(i)}y^{(j)}x^{(i)^T}x^{(j)}-\sum_{i=1}^m\beta_i\)
- \(s.t.: \sum_{i=1}^m\beta_iy^{(i)}=0\)
- \(\quad \beta_i\geq0,i=1,2,\cdots,m\)
\(\beta\)求解采用SMO方法
SVM的软间隔模型
硬间隔:可以认为线性划分SVM中距离度量就是硬间隔,最大化硬间隔条件为:
- \(min_{w,b}\frac{1}{2}||w||_2^2\)
- \(s.t. \quad y^{(i)}(w^Tx^{(i)}+b)\geq1,i=1,2,\cdots,m\)
软间隔:SVM对于训练集的每个样本引入一个松弛因子(ξ),使得函数距离加上松弛因子(ξ)后的值大于等于1;
- \(y^{(i)}(w^Tx^{(i)}+b)\geq1-ξ,i=1,2,\cdots,m,ξ_i\geq0\)
- 如果松弛因子大于1,那么表示允许该样本点分错,所以说加入松弛因子是有成本的。所以最终目标函数转换为:
- \(min_{w,b}\frac{1}{2}||w||_2^2 +C\sum_{i=1}^mξ_i\)
- \(s.t. \quad y^{(i)}(w^Tx^{(i)}+b)\geq1,i=1,2,\cdots,m\)
- 函数中的C>0是惩罚参数,是一个超参数,C越大表示对误分类的惩罚越大
软间隔对应的拉格朗日函数:
- \(L(w,b,ξ,\beta,\mu)=\frac{1}{2}||w||^2_2 +C\sum_{i=1}^mξ_i+\sum_{i=1}^m\beta_i[1-ξ_i-y^{(i)}(w^Tx^{(i)}+b)]-\sum_{i=1}^m\mu_iξ_i,\beta \geq0,\mu_i\geq0\)
优化目标变成:
- \(min_{w,b,ξ}max_{\beta,\mu}Lw,b,ξ,\beta,\mu)\)
根据拉格朗日对偶性特性,化为等价的对偶问题,则优化目标为:
- \(max_{\beta,\mu}min_{w,b,ξ}L(w,b,ξ,\beta,\mu)\)
使函数L极小化求w、b、ξ的取值:
- \(\frac{\partial L}{\partial w}=0\rightarrow w-\sum_{i=1}^m\beta_iy^{(i)}x^{(i)}=0\rightarrow w=\sum_{i=1}^m\beta_i y^{(i)}x^{(i)}\)
- \(\frac{\partial L}{\partial b}=0\rightarrow -\sum_{i=1}^m\beta_iy^{(i)}=0\rightarrow \sum_{i=1}^m\beta_i y^{(i)}=0\)
- \(\frac{\partial L}{\partial ξ}=0\rightarrow C-\beta_i-\mu_i=0\)
将w,b,ξ带入优化函数L中,优化函数为:
- \(l(\beta)=\sum_{i=1}^m\beta_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\beta_i\beta_jy^{(i)}y^{(j)}x^{(i)^T}x^{(j)}\)
\(max l(\beta)\rightarrow min-l(\beta),\)优化函数为:
- \(min\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\beta_i\beta_jy^{(i)}y^{(j)}x^{(i)^T}x^{(j)}-\sum_{i=1}^m\beta_i\)
- \(s.t: \sum_{i=1}^m\beta_iy^{(i)}=0\)
- \(\quad C-\beta_i-\mu_i=0\)
- \(\quad \beta_i\geq0,i=1,2,\cdots,m\)
- \(\quad \mu_i\geq0,i=1,2,\cdots,m\)
整理后的函数,软硬间隔的优化函数一致,只条件不同:
- \(min\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\beta_i\beta_jy^{(i)}y^{(j)}x^{(i)^T}x^{(j)}-\sum_{i=1}^m\beta_i\)
- \(s.t: \sum_{i=1}^m\beta_iy^{(i)}=0\)
- \(\quad 0\leq\beta_i<C,i=1,2,\cdots,m\)
\(\beta\)求解采用SMO方法
SVM 线性不可分
如果将数据映射到高维空间中,那么数据就会变成线性可分的,从而就可以使用线性可分SVM模型或者软间隔线性可分SVM模型
- \(min\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\beta_i\beta_jy^{(i)}y^{(j)}\phi(x^{(i)})\cdot\phi(x^{(j)})-\sum_{i=1}^m\beta_i\)
- \(s.t: \sum_{i=1}^m\beta_iy^{(i)}=0\)
- \(\quad 0\leq\beta_i<C,i=1,2,\cdots,m\)
- \(\phi\):定义的一个从低维特征空间到高维特征空间的映射函数
直接采用映射,会产生维度爆炸
核函数
核函数是从低维特征空间到高维特征空间的一个映射。
- 核函数可以自定义:核函数必须是正定核函数,即Gram矩阵是半正定矩阵
- 核函数的价值在于:它事先在低维空间上进行计算,而将实质上的分类效果表现在高维上。
- 通过核函数,可以将非线性可分的数据转换为线性可分数据
核函数分类:
- 线性核函数:
- \(K(x,z)=x\cdot z\)
- 多项式核函数
- \(K(x,z)=(\gamma x\cdot z+r)^d\)
- 高斯核函数
- \(K(x,z)=e^{-\gamma ||x-z||^2_2}\)
- sigmoid函数:
- \(K(x,z)=tanh(\gamma x\cdot z+r)\)
高斯核函数证明:
- \(K(x,z)=e^{-\gamma ||x-z||^2_2}\)
- \(=e^{-\gamma ||x||^2_2}e^{-\gamma ||z||^2_2}(\sum^{+\infty}_{i=0}\frac{(2\gamma x\cdots z)^i}{i!})\)
- \(=\sum^{+\infty}_{i=0}(e^{-\gamma ||x||^2_2}e^{-\gamma ||z||^2_2}(\frac{(2\gamma x\cdots z)^i}{i!}))\)
- \(=\sum^{+\infty}_{i=0}(e^{-\gamma ||x||^2_2}e^{-\gamma ||z||^2_2}\sqrt{\frac{(2\gamma)^i}{i!}}\sqrt{\frac{(2\gamma)^i}{i!}}||x||_2^i||z||_2^i)\)
- \(\phi(x)\cdot\phi(z)\)
序列最小优化算法SMO
拉格朗日乘子法和KKT的对偶互补条件为:
- \(\beta_i(y^{(i)}(w^Tx^{(i)}+b)-1+ξ_i)=0\)
- \(u_iξ_i=0\)
\(\beta,\mu,C\)之间的关系为:\(C-\beta_i-u_i=0\)
根据对偶互补条件可得以下关系式:
- \(\beta_i=0\rightarrow \mu_i>0\rightarrowξ_i=0\rightarrow y^{(i)}(w^Tx^{(i)}+b)\geq1\)
- \(0<\beta_i<C\rightarrow \mu_i>0\rightarrowξ_i=0\rightarrow y^{(i)}(w^Tx^{(i)}+b)=1\)
- \(\beta_i=C\rightarrow \mu_i=0\rightarrowξ_i\geq0\rightarrow y^{(i)}(w^Tx^{(i)}+b)\leq1\)
也就是要找到的最优分割超平面必须满足以下的目标条件\(g(x)\):
- \(y^{(i)}g(x^{(i)})\geq1,\{(x^{(i)},y^{(i)})|\beta_i=0\}\)
- \(y^{(i)}g(x^{(i)})=1,\{(x^{(i)},y^{(i)})|0<\beta_i<C\}\)
- \(y^{(i)}g(x^{(i)})\geq1,\{(x^{(i)},y^{(i)})|\beta_i=C\}\)
拉格朗日对偶化要求的两个限制的初始条件为
- \(\sum_{i=1}^m\beta_iy^{(i)}=0\)
- \(0\leq\beta_i\leq C,i=1,2,\cdots,m\)
从而得到解决问题的思路:
- 初始化一个\(\beta\)值,让它满足对偶条件的两个初始限制条件
- 不断优化\(\beta\)值,使得由他确定的分割超平面满足满足g(x)目标条件;且在过程中,始终保证\(\beta\)值满足初始限制条件
- 注意:求解过程中,是让g(x)目标条件尽可能的满足
求解第一步:选择\(\beta\)值
SMO是选择两个合适的β变量做迭代,其它变量作为常量来进行优化的一个过程,选择\(\beta\)值遵循以下两个原则:
- 每次优化的时候,必须同时优化β的两个分量;因为如果只优化一个分量的话,新的β值就没法满足初始限制条件中的等式约束条件了。
- 每次优化的两个分量应该是违反g(x)目标条件比较多的。也就是说,本来应当是大于等于1的,越是小于1违反g(x)目标条件就越多。
第一个\(\beta\)选择:
- 一般情况下,先选择0<β<C的样本点(即支持向量),只有当所有的支持向量都满足KKT条件的时候,才会选择其它样本点。
- 原因:选择的样本点违反KKT条件最严重,可以以更少的迭代次数让模型达到g(x)目标条件
- \(y^{(i)}g(x^{(i)})\geq1,\{(x^{(i)},y^{(i)})|\beta_i=0\}\)
- \(y^{(i)}g(x^{(i)})=1,\{(x^{(i)},y^{(i)})|0<\beta_i<C\}\)
- \(y^{(i)}g(x^{(i)})\geq1,\{(x^{(i)},y^{(i)})|\beta_i=C\}\)
第二个\(\beta\)选择:
- 在选择第一个变量\(\beta_1\)后,在选择第二个变量\(\beta_2\)的时候,希望能够按照优化后的\(\beta_1\)和\(\beta_2\)有尽可能多的改变来选择,也就是说让|\(E_1\)-\(E_2\)|足够的大,当\(E_1\)为正的时候,选择最小的\(E_i\)作为\(E_2\);当\(E_1\)为负的时候,选择最大的\(E_i\)作为\(E_2\)。
- 备注:如果选择的第二个变量不能够让目标函数有足够的下降,那么可以通过遍历所有样本点来作为\(\beta_2\),直到目标函数有足够的下降,如果都没有足够的下降的话,那么直接跳出循环,重新选择\(\beta_1\);
- \(E_i=g(x^{(i)})-y^{(i)}\)
求解第二步:优化\(\beta\)值
目标函数:
- \(min\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\beta_i\beta_jy^{(i)}y^{(j)}K(x^{(i)},x^{(j)})-\sum_{i=1}^m\beta_i\)
- \(s.t: \sum_{i=1}^m\beta_iy^{(i)}=0\)
- \(\quad 0\leq\beta_i<C,i=1,2,\cdots,m\)
认为\(\beta_1\),\(\beta_2\)是变量,其他\(\beta\)值为常量,目标函数转换如下:
- \(min_{\beta_1,\beta_2}\frac{1}{2}K_{11}\beta_1^2 + \frac{1}{2}K_{22}\beta_2^2+K_{12}y^{(1)}y^{(2)}\beta_1\beta_2-\beta_1-\beta_2+y^{(1)}\beta_1\sum_{i=3}^my^{(i)}\beta_iK_{i1}+y^{(2)}\beta_2\sum_{i=3}^my^{(i)}\beta_iK_{i2}\)
- \(s.t: \beta_1y^{(1)}+\beta_2y^{(2)}=-\sum_{i=3}^m\beta_iy^{(i)}=k\)
- \(\quad 0\leq\beta_i<C,i=1,2\)
由于\(\beta_1y^{(1)}+\beta_2y^{(2)}=k\),且\(y^2=1\),用\(\beta_2\)表示\(\beta_1\):
- \(\beta_1=y^{(1)}(k-\beta_2y^{(2)})\)
带入目标优化函数,消去\(\beta_1\),可得:
- \(W(\beta_2)=\frac{1}{2}K_{11}(k-\beta_2y^{(2)})^2 + \frac{1}{2}K_{22}\beta_2^2+K_{12}y^{(2)}(k-\beta_2y^{(2)})\beta_2-y^{(1)}(k-\beta_2y^{(2)})-\beta_2+(k-\beta_2y^{(2)})v_1+y^{(2)}\beta_2v_2\)
- \(v_j=\sum_{i=3}^my^{(i)}\beta_iK_{ij}\)
求导:
- \(\frac{\partial W}{\partial\beta_2}=K_{11}\beta_2-K_{11}ky^{(2)}+K_{22}\beta_2 +K_{12}ky^{(2)}-2K_{12}\beta_2+y^{(1)}y^{(2)}-1-y^{(2)}v_1+y^{(2)}v_2\)
令导数为0:
- \((K_{11}+K_{22}-2K_{12})\beta_2=y^{(2)}(y^{(2)}-y^{(1)}+kK_{11}-kK_{12}+v_1-v_2)\)
- \(=y^{(2)}(y^{(2)}-y^{(1)}+kK_{11}-kK_{12}+(g(x_1)-\sum_{i=1}^2\beta_iy^{(i)}K_{i1}-b)-(g(x_2)-\sum_{i=1}^2\beta_iy^{(i)}K_{i2}-b)\)
将\(k=\beta_1y^{(1)}+\beta_2y^{(2)}\)带入得:
- \((K_{11}+K_{22}-2K_{12})\beta_2=y^{(2)}(y^{(2)}-y^{(1)}+\beta_1^{old}y^{(1)}K_{11}+\beta_2^{old}y^{(2)}K_{11}-\beta_1^{old}y^{(1)}K_{12}-\beta_2^{old}y^{(2)}K_{12}+y^{(2)}(g(x_1)-\sum_{i=1}^2\beta_i^{old}y^{(i)}K_{i1}-b)-y^{(2)}(g(x_2)-\sum_{i=1}^2\beta_i^{old}y^{(i)}K_{i2}-b)\)
- \(=y^{(2)}((K_{11}-2K_{12}+K_{22})\beta_2^{old}y^{(2)}+y^{(2)}-y^{(1)}+g(x^{(1)})-g(x^{(2)}))\)
- \(=(K_{11}-2K_{12}+K_{22})\beta_2^{old}+y^{(2)}[(g(x^{(1)})-y^{(1)})-(g(x^{(2)})-y^{(2)})]\)
令\(E_i=g(x^{(i)})-y^{(i)}\)
- \(\beta_2^{new,unt}=\beta_2=\beta_2^{old}+\frac{y^{(2)}(E_1-E_2)}{K_{11}+K_{22}-2K_{12}}\)
考虑\(\beta_1\),\(\beta_2\)的取值限定范围,假定新求出来的β值是满足我们的边界限制的,即,
-
\(L\leq\beta_2^{new}\leq H\)
-
当\(y_1=y_2\)的时候,\(\beta_1\)+\(\beta_2=k\),由于\(\beta\)的限制条件,可得
- \(L=max(0,\beta_2^{old}+\beta_1^{old}-C)\)
- \(H=min(C,\beta_2^{old}+\beta_1^{old})\)
- 限制条件:
- \(0\leq k-\beta_2^{new}\leq C\)
- \(0\leq \beta_2^{new}\leq C\)
-
当\(y_1\neq y_2\)的时候,\(\beta_1\)-\(\beta_2=k\),由于\(\beta\)的限制条件,可得
- \(L=max(0,\beta_2^{old}-\beta_1^{old})\)
- \(H=min(C,C+\beta_1^{old}-\beta_2^{old})\)
- 限制条件:
- \(0\leq k-\beta_2^{new}\leq C\)
- \(0\leq \beta_2^{new}\leq C\)
结合β的取值限制范围以及函数W的β最优解,我们可以得带迭代过程中的最优解为:
- \(\beta_2^{new}=H;\beta_2^{new,unt}>H\)
- \(\beta_2^{new}=\beta_2^{new,unt};L\leq \beta_2^{new,unt}\leq H\)
- \(\beta_2^{new}=L;\beta_2^{new,unt}\leq L\)
根据\(\beta_1\),\(\beta_2\)的关系,可得\(\beta_1\)迭代后的值:
- \(\beta_1^{old}y^{(1)}+\beta_2^{old}y^{(2)}=\beta_1^{new}y^{(1)}+\beta_2^{new}y^{(2)}\rightarrow \beta_1^{new}=\beta_1^{old}+ y^{(1)}y^{(2)}(\beta_2^{old}-\beta_2^{new})\)
求解第三步:计算阈值和差值E
在每次完成两个β变量的优化更新之后,需要重新计算阈值b和差值\(E_i\)
- \(0\leq \beta^{new}\leq C \rightarrow y^{(1)}-\sum_{i=1}^m\beta_iy^{(i)}K_{i1}-b_1=0\)
化简为:\(b^{new}=\frac{b_1^{new}+b_2^{new}}{2}\)
更新后的差值\(E_i\):
- \(E_i=g(x^{(i)})-y^{(i)}=\sum_{j=3}^m\beta_jy^{(i)}K_{ij}+\beta_1^{new}y^{(1)}K_{11}+\beta_2^{new}y^{(2)}K_{12}+b^{new}-y^{(1)}\)
SVR
待补充
Python实现
待补充

 浙公网安备 33010602011771号
浙公网安备 33010602011771号