第一部分到第三部分

注意：综合张雨石笔记和中文讲义学习，中文讲义有一些概念翻译不准确。

1.关于trace性质的证明见ML公开课笔记附录。

2.非参数算法的定义更直观来讲应该是：参数数量随着数据集规模的增长而增长。

3.似然性(likelihood)和概率(proability)两个概念大体上是相同的，似然性强调L(θ)是θ的函数，而概率强调是数据的函数。所以我们经常说“数据的概率，参数的似然性”。(Probability of data, likelihood of parameter)。

4.广义线性模型中的线性：是指假设3，即自然参数η和输入值x是线性相关的。

5.广义线性模型的好处是，如果我有一个需要预测的量y，只有0和1两种值，那么我选择了伯努利分布，之后的预测模型的得出都是自动进行的。

6.在数学推导的《线性回归与最小二乘法》一文中，矩阵偏导使用的是分子布局，与这篇文章的布局一致。另外附上：讲解2

第四部分生成学习

1.argmax：求函数达到最大值时对应的自变量值。

2.半正定矩阵是正定矩阵的推广。实对称矩阵A称为半正定的，如果二次型X'AX半正定，即对于任意不为0的实列向量X，都有X'AX≥0。(正定矩阵是>0）。

3.NB的关于三个参数的意义：p(x|y=1)是统计垃圾邮件中出现相应单词的邮件比例，p(x|y=0)是正常邮件中出现相应单词的邮件比例，p(y)是垃圾邮件概率（因为是Bernoulli分布），由此可以由p(y|x)=p(x|y)p(y)预测给定相应单词是垃圾邮件的概率。

4.多项式事件模型中，p(y)是邮件的种类标签对应的概率，这是首先要被选中的，然后是对应各个词的概率。用到的参数Φ(k|y=1)意为当一个人决定向你发送垃圾邮件时选用词典中下标为k的词的概率。

5.多项式事件模型中，参数的最大似然估计，Φ(k|y=1)公式中m是邮件数量，ni是词典中的词总数。分子意思是垃圾邮件中对应单词出现的次数，分母是垃圾邮件的单词总数之和，也就是把所有垃圾邮件展开一维的总长。所以这个比值的意思就是所有垃圾邮件中词k所占的比例。

第五部分支持向量机

1.拉格朗日乘数法回顾。

2.张雨石笔记6最后几何间隔的定义其实是一个简化的SVM，s.t.后的内容是约束条件，该集合的点均需要满足左式也就是各点几何间隔的结果均大于我们选定的L，且w正则化为1，在此基础上找到最大的L，就是集合的几何间隔。

3.支持向量机的思路部分数学推导pdf讲解最为清楚。

4.关于下式的理解：如果gi(w)违反了约束条件，比如gi(w)>0，那么只要我的αi无穷大，就可以满足maxL的目的，所以这时的θp就会是无穷大。至于符合条件的θp为什么是f(w)，因为符合条件时hi(w)=0，gi(w)<=0，而规定了αi>=0，所以L最大值一定是f(w)。那么为什么要引入αi和βi？因为它们将约束条件加入到了一个式子中，这样只用关心w就可以了。

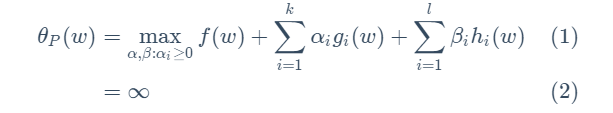
5.“训练样本的函数边界确定为1”：y(wx+b)=1，即数学推导pdf开头所示。

6.核函数部分：在K=(xz)^2例子中，n=3，Φ(x)里有9个元素，所以计算量是O(n^2)量级，但是K的计算只需要(xz)^2，也就是取出x,z下标对应的元素相乘后平方，是O(n)量级。

7.关于软间隔分类器：ξi≥0说明允许一些点的1-ξi<0，因为yi(wx+b)<0就意味着误分类，所以软间隔分类器是允许一些误分类的点的，但是此时要在C∑ξi中增加惩罚项。

8.SMO中Minimal的意思是我们每一次只调节最少数量的参数，通过顺序迭代逐步优化。

第六部分学习理论

1.如果一个字母有"hat"，表示是对某一个量的估计值。

2.关于下式：第一个不等号是一致收敛定理，真实值和估计值最多相差γ，第二个不等号是因为h hat的定义对应最小的训练误差，所以对于训练误差来说，h hat就是最小的。ε hat是training error，意为给定h hat，误分类样本在总训练集合中所占的比例。generalization error of h(ε h)的意思是给定假设h，根据分布D采样得到一个新的样本，对这个样本误分类的概率。h hat是由ERM选取的假设，是ERM假设类中对应最小训练误差的那个假设。

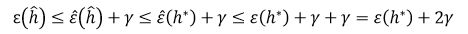
第七部分正则化与模型选择

1.VC位：在二维平面中，当然三个点组成的集合也有不能被分散的情况（比如集合规则为在一条直线上时），但是只要存在一种规则的三个点的集合可以被分散，那么VC维就可以是3。

2.ERM的直观意义中，如果z也就是hθ(x)<0，那么预测就是正确的，如果>0，那么I=1，预测就是错误的。我希望这个值尽量小，所以也就是hθ(x)<0。logistic函数logP(y(i)/x(i);θ)就是对ERM的一个凸性近似，从而变成一个凸优化问题。SVM也是一个分段函数，在比较小的时候为0，之后线性增大。

3.特征选择的思路：计算一个简单的分数 $x_i 对分类标签(class labels) y所能体现的信息量。然后，只需根据需要选择最大分数S(i)的 k个特征。$