L4.a
L4.a
电磁感应基本原理探讨
可直接跳转到“不同参考系中的动生电动势”小节开始阅读,Test部分是我从知乎摘录的,可能不甚准确或解释不够清晰。
Test
感生电动势:放在变化磁通量中的导体会产生感应电动势。
原理:
-
静电场:由静止电荷产生的电场。
性质:保守场/无旋场,沿电场的闭合回路积分=0. -
涡旋电场和磁场:考虑一个匀速运动的电荷,和一个与该电荷存在相对速度的检验电荷。
$$\begin{equation} \begin{aligned} F&=\text{速度无关项}+\text{速度相关项}\\ &=\text{磁场力}+\text{感应电场力}\\ &=q\vec{v}\times \vec{B}+q\vec{E} \end{aligned} \end{equation}$$
设定一个参考系,该检验电荷所受的,来自匀速运动电荷的作用力表示为:这里,$\vec{B}$称为磁感应强度或磁场,$\vec{v}$是检验电荷在参考系中的速度矢量,q是检验电荷的电量;
E称为涡旋电场,不是静电场,在场中对E积一圈分结果不为零。
从这里可以看出,当检验电荷速度为0时,磁场力也为0. -
电流产生的场:由于电流实际上是由一大堆连续运动的电荷组成的,因此电流也会对其他电荷产生力的作用。
讨论2种电流:- 稳恒电流:电流不变,当一个电荷从它的原本位置流走时,马上又会有另一个电荷填上这个位置。
这样对于流过一圈闭合路径的电荷,空间中这一圈的任何位置,好像一直都放着同样多的电荷。
因此,稳恒电流产生的电场类似静电场,同样是保守的。
这里注意,因为电子是负的,而组成导线的正离子是正的,它们的电场中和掉了,所以只有电流产生的磁场对外界有效果。 - 非稳恒电流:由于电流变化,其产生的磁场是“有旋的”,即随着电流变化而变化。
- 稳恒电流:电流不变,当一个电荷从它的原本位置流走时,马上又会有另一个电荷填上这个位置。
-
感应电场的产生:
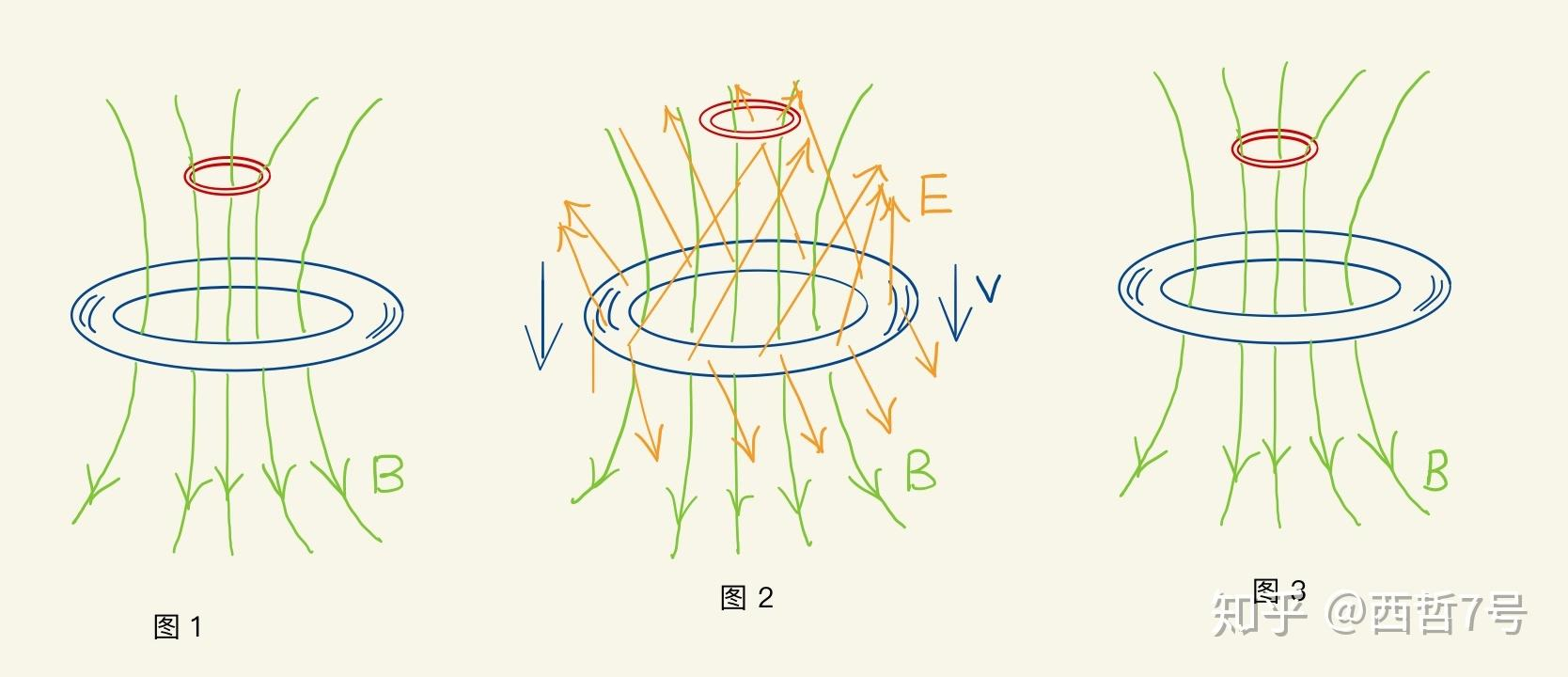
考虑如下图所示的情况,已知蓝色的大线圈A上通了稳恒电流,在其上方悬挂有一个小线圈B。
![image]()
- 若两导线圈相对静止,虽然线圈A能产生稳恒磁场和稳恒电场,但稳恒电场被导线体电场中和掉,因此只有稳恒磁场B显露;
- 当线圈A向下移动时,A和B之间存在一个相对速度,参考点2“涡旋电场和磁场”部分。
若设定一个和B相对静止的参考系,线圈A以某速度向下移动,而A中的电流将变成螺旋向下的流动,该电流产生的电场不是稳恒电场,而是“涡旋电场”。
这个新的电场无法被导体的静电场中和掉,会显露出来。
涡旋电场会在B当中产生一个电动势,同时线圈A这样变化的电流将产生一个变化的磁场,该磁场将整体向下移。 - 当线圈A停下时,A、B回到相对静止状态,涡旋电场变成稳恒电场、变化的磁场变成稳恒磁场。
- 我们可以把上述感应电动势的产生概述为:A 的变化电流会产生涡旋电场,从而在 B 中产生电动势。
注意到变化的电流也会产生变化的磁场,因此可以用变化的磁场体现变化的电流,从而量化线圈B当中电动势产生的多少。
-
动生电动势和感生电动势的统一:
-
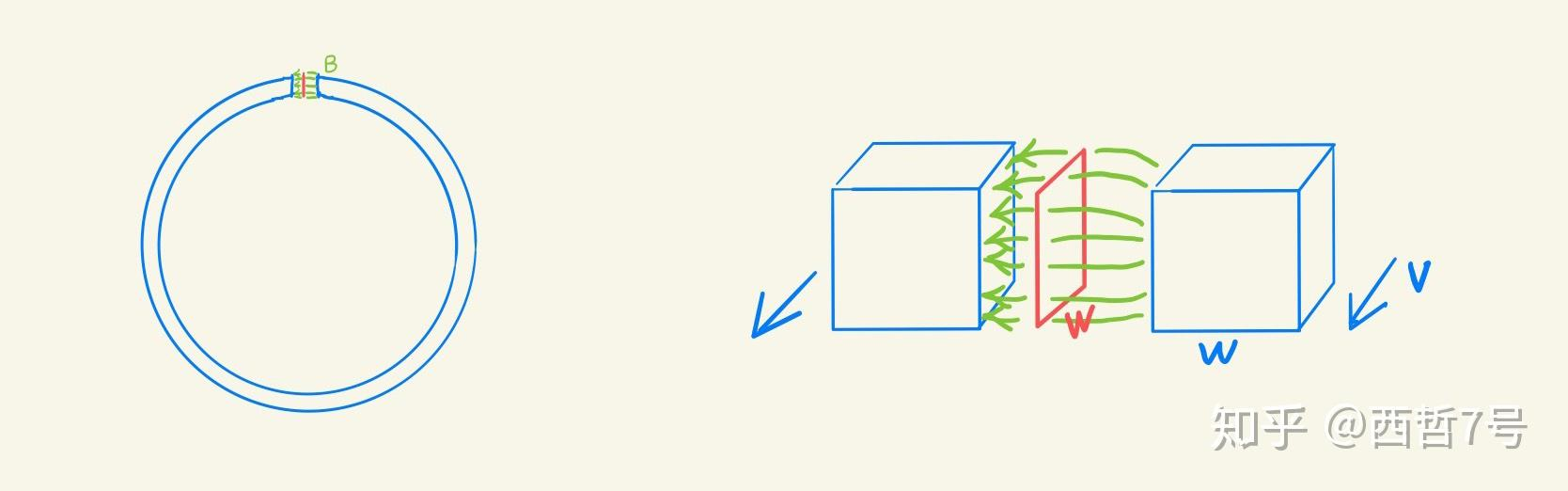
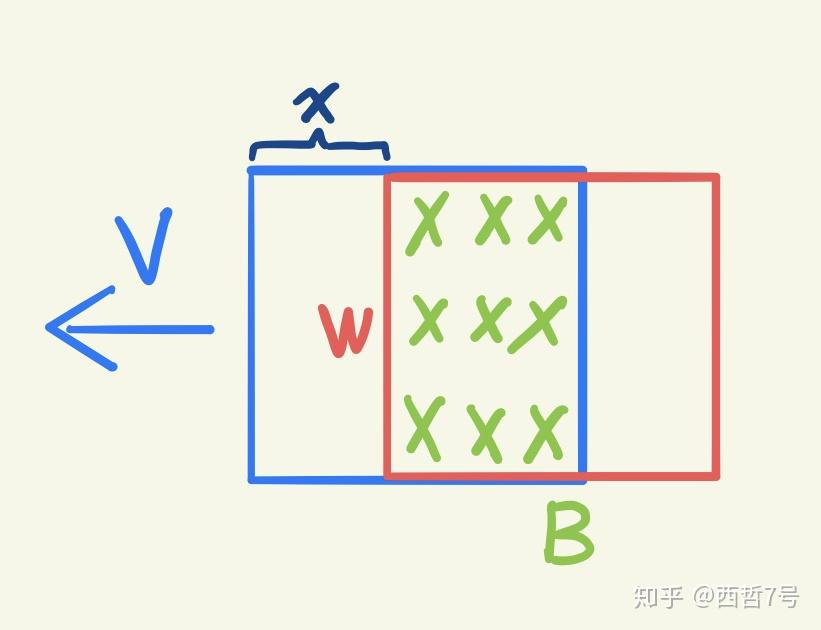
考虑如下情境,其中红色的线圈是固定的,蓝色的磁铁可相对线圈运动。
![image]()
-
若当前参考系相对线圈静止,那么由于磁铁相对于线圈存在速度,则磁场会随着磁铁的位置变化,变化的磁场体现了变化的电流,线圈中将产生感生电动势。
$$\begin{equation}S=w^2-xw\end{equation}$$
计算线圈中电动势的过程如下,基于磁通量变化求解:
![image]()
设磁铁口和线圈面相截的面积为S,则有:磁通量:
$$\begin{equation} \Phi=\iint_S\overrightarrow{B}\bullet\overrightarrow{dS}=B\iint_SdS=BS=B(w^2-xw) \end{equation}$$感生电动势强度:
$$\begin{equation} \varepsilon=-\frac{d\Phi}{dt}=-B\frac{d}{dt}(w^2-xw)=wB\cdot\frac{dx}{dt}=wBv \end{equation}$$ -
若当前参考系和磁铁相对静止,此时磁铁开口处提供均匀、恒定的磁场,线圈存在和磁铁的相对速度,线圈中的电子受到该磁场的洛伦兹力,从而产生电动势。
$$\begin{equation}\begin{aligned} \varepsilon&=\oint_{L}(\overrightarrow{v}\times\overrightarrow{B})\bullet\overrightarrow{dl}=\int_{\text{里}}(\overrightarrow{v}\times\overrightarrow{B})\bullet\overrightarrow{dl}\\ &=\int_\text{里}vB\mathrm{~}dl=vB\int_\text{里}dl=vBw \end{aligned}\end{equation}$$
动生电动势的计算步骤如下:
-
为什么静止电荷能产生一个场?
- 吸引正电荷、排斥负电荷。
为什么洛伦兹力能导致导体内产生电荷分离,进而形成电场,在闭合回路中的表现是感生电动势?(已知:导体中的自由电子在磁场中运动,受到洛伦兹力;由于电子在导体的晶格结构中运动,受洛伦兹力影响的电子和晶格结构碰撞,把电子所受的力传递给整个导体。)
- 由于电子带负电,洛伦兹力使得其向导体一侧移动,而正离子固定在晶格中,导致电荷分离。
在公式$F=q\vec{v}\times \vec{B}+q\vec{E}$中,我们一般认为$\vec{v}\times \vec{B}=\vec{E}$,为什么F公式里面还有一个E?
- $\vec{v}\times \vec{B}$是磁场,单独的$\vec{E}$是电场,认为B和E二者是独立于匀速运动电荷和检验电荷的,由外部力量施加的场?还是说,这里的电场是来自运动电荷的静电场?
因为电子是负的,而组成导线的正离子是正的,它们的电场中和掉了,所以只有电流产生的磁场对外界有效果,这是为什么呢?
- 在稳恒电流的导线中,电子移动形成电流,正离子固定,正负电荷总数相等、分布均匀,其产生的静电场在导线外部相互抵消,因此净电场接近0。
不同参考系中的动生电动势
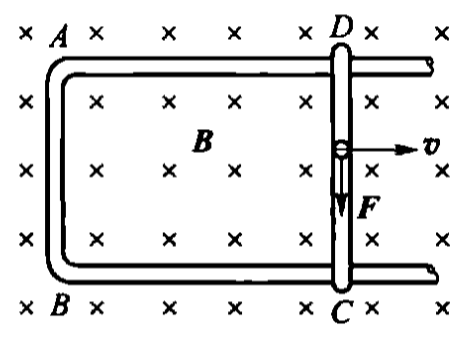
情境:一根导体棒CD,长度为L,在外部机械力驱动下,以速度v向右运动,它和一个U形导体构成闭合回路,场景中存在强度为B且指向纸面的磁场。
设定x轴正方向为右(即导体棒运动方向),y轴正方向向上,磁场指向z轴正方向(即指向纸面)。三个正方向的单位向量为$\hat{i}$,$\hat{j}$,$\hat{k}$。
-
实验室参考系固定(S系):无外加电场,有外加磁场。
-
定性分析:外部机械力维持导体运动,导体内部的自由电子(负电荷)跟随导体运动;
受洛伦兹力作用,用右手定则判断出,电子受到的力沿y轴负方向,因此电子向C端聚集,C端带负电,D端带正电。
这样,通过电荷分离,产生一个静电场,就把外部提供的机械能转化为了回路内的电势能。
此时,CD就起到了电源的作用,即作为非静电力做功的媒介:-
系统达到平衡时,稳恒电流必须是闭合的,当电荷沿闭合回路绕行1周后,所经历的总的电势改变为零,即在闭合回路中,如果有电势下降的路段,就必有电势上升的路段;
当正电荷沿电势下降的路段(电源外电路)运动时,静电力做功,电荷的电势能减小,转化为热能(焦耳定律,$P=\frac{Q}{\Delta t}=I^{2}R=\frac{U^{2}}{R}$)或其他形式(如电流通过电动机、扩音器等),好比从滑梯上滑下的劳G受到重力、摩擦力、空气阻力等作用,重力势能转化为动能、热能;
当正电荷沿电势上升的路段运动时,电荷的电势能增加,静电力将对电荷的运动起阻碍作用(就像上升的气球受到重力阻碍),同时电荷的运动还受到导体内部的阻碍,在这种双重阻碍下,正电荷沿电势上升路段的定向运动将逐步减速;
此时,正电荷无法回到电势能较高的原来位置,电荷出现堆积,电流随时间变化,电流的闭合性遭到破坏,稳恒电流无法维持。
所以,需要有一种非静电本质的力作用于电荷,逆电场方向运动,来让正电荷回到电势能较高的原来位置,提供这种力的装置就叫电源,就像劳G需要一个外力帮忙以返回高处滑梯的顶端,逆着引力场方向运动,以重复下滑运动。 -
导体棒通过洛伦兹力(一种非静电力)将机械能转化为电能,虽然洛伦兹力本身不直接对电子做功(因其垂直于速度),但外部机械力维持导体运动,间接通过电荷分离做功。
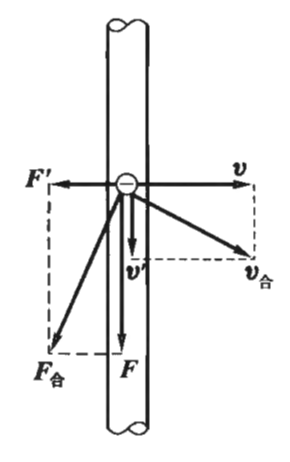
这里对洛伦兹力在移动导体棒上的作用做进一步分析:
![image]()
- 导体棒内自由电子的速度,由随导线向右的速度v,和受洛伦兹力向下运动、形成感应电流的速度v'组成;
- 自由电子所受洛伦兹力$F_{合}=-ev_{合}\times B$也可分成两部分,一个是和v相应的$F=-evB$,向下(右手定则);另一个是和v'相应的$F'=-ev'B$,向左;
- F和导线平行,它沿导线的积分表现为动生电动势,充当电源中的非静电力,电子在F作用下有沿着导线的速度v',故F对电子做正功Fv';
F'和导线垂直,宏观上表现为导线受到的安培力,和导线平移速度v反向,做负功F'v; - 易证明Fv'=-F'v,故两个力作的总功为零,即洛伦兹力的每一部分都做了功,但两个功的代数和为零。
-
-
定量分析:
$$\begin{equation}\large\vec{F_L}=-e(\vec{v}\times\vec{B})=-e(v\hat{i}\times B\hat{k})=-evB\hat{j}\end{equation}$$
洛伦兹力作用:自由电子速度$\vec{v}=v\hat{i}$,据洛伦兹力公式有:电荷分离产生静电场$\vec{E}_s$,当系统达到平衡,静电场力$\vec{F}_e=-e\vec{E}_s$应当和洛伦兹力相等,因为系统中没有别的作用力了:
$$\begin{equation} \begin{aligned}-e\vec{E}_s=-e(\vec{v}\times\vec{B})\\\vec{E}_s=\vec{v}\times\vec{B}=vB\hat{j}\end{aligned} \end{equation}$$得到单位长度导体的静电场强度后,积分可得导体CD两端的电势差(即动生电动势强度,其中D端电势高于C端):
$$\begin{equation} V=\int_C^D\vec{E}_s\cdot d\vec{l}=\int_0^LvB\mathrm{~}dy=vBL \end{equation}$$
-
-
导体静止参考系固定(S'系):仅考虑静态场,不考虑动态电磁场的传播。
-
定性分析:根据狭义相对论,电场和磁场在不同惯性系之间,可通过洛伦兹变换转换。
狭义相对论基于如下两个基本原则:- 相对性原理:物理定律在所有惯性系中的形式相同。
- 光速不变性:真空中的光速c在任何惯性系中均为常数,与光源或观察者的运动无关。
经典电磁学的基石是麦克斯韦方程组,它在任何惯性系中保持相同的数学形式,这和狭义相对论的原则相符合,因此我们可以使用洛伦兹变换,在不同惯性系之间,对静态的电磁场进行转换。
注意,结合狭义相对论和麦克斯韦方程组,我们可知,电场和磁场并不是独立的实体,而是同一电磁场的不同表现。
-
定量分析:
-
麦克斯韦方程组:
$$\begin{equation}\left\{\begin{matrix}\nabla\boldsymbol{\bullet}\boldsymbol{D}=\rho_0(电场发散)\\ \nabla\times\boldsymbol{E}=-\frac{\partial\boldsymbol{B}}{\partial t}(法拉第感应)\\ \nabla\boldsymbol{\bullet}\boldsymbol{B}=0(磁场无源)\\ \nabla\times\boldsymbol{H}=\boldsymbol{j}_0+\frac{\partial\boldsymbol{D}}{\partial t}(安培-麦克斯韦定律)\end{matrix}\right.\end{equation}$$或另一形式:
$$\begin{equation}\begin{aligned}&\nabla\cdot E=4\pi\rho\\&\begin{aligned}\nabla\cdot B=0\end{aligned}\\&\nabla\times E=-\frac{1}{c}\frac{\partial B}{\partial t}\\&\nabla\times B=\frac{4\pi}{c}J+\frac{1}{c}\frac{\partial E}{\partial t}\end{aligned}\end{equation}$$解析:
- 电场发散:库仑定律的高级表达。
电场线从正电荷发出,终止于负电荷,或在无穷远处消失。
$\mathbf{D}$是电位移矢量,表示电场在介质中的总效应($\text{C}/\text{m}^2$),在真空中,$\mathbf{D}=\epsilon_0\mathbf{E}$,其中$\epsilon_0$是真空介电常数($\approx 8.85\times 10^{-12}~\text{F}/\text{m}$),$\mathbf{E}$是电场强度($\text{V}/\text{m}$);
$\rho_0$是自由电荷密度($\text{C}/\text{m}^3$),表示单位体积内的自由电荷量,$\nabla\boldsymbol{\bullet}\boldsymbol{D}$是电位移的散度,表示电场线的净流入或流出。 - 法拉第感应:磁场随时间的变化会在空间中激发出“旋度电场”(即涡旋电场),其方向与磁场变化率相反。
$\nabla\times\boldsymbol{E}$是电场的旋度,$-\frac{\partial\boldsymbol{B}}{\partial t}$是磁场的时间变化率。 - 磁场无源:磁场没有源头,即不存在磁单极子,磁场线总是从北极到南极形成回路,是闭合的,没有净流入或流出。
$\boldsymbol{B}$是磁感应强度,$\nabla\boldsymbol{\bullet}\boldsymbol{B}$是磁场的散度。 - 安培-麦克斯韦定律:电流和变化的电场都会激发磁场。
$\boldsymbol{H}$是磁场强度($\text{A}/\text{m}$),在真空中$\boldsymbol{H}=\frac{\boldsymbol{B}}{\mu_0}$,$\mu_0$是真空磁导率,$\nabla\times\boldsymbol{H}$是磁场的旋度;
$\textbf{j}_0$是自由电流密度($\text{A}/\text{m}^2$),$\frac{\partial\boldsymbol{D}}{\partial t}$是位移电流密度($\text{A}/\text{m}^2$,代表变化的电场,见电场发散部分)。
- 电场发散:库仑定律的高级表达。
-
电磁场的相对论变换:取方程组中式2、3,分别在S系和S'系中写成分量形式,利用四维微分算符变换,得到的结果为:
$$\begin{equation} \begin{cases} E_x' = E_x,\\ E_y' = \gamma\,(E_y - v B_z),\\ E_z' = \gamma\,(E_z + v B_y), \end{cases} \end{equation}$$$$\begin{equation} \begin{cases} B_x' = B_x,\\ B_y' = \gamma\!\Bigl(B_y + \frac{v}{c^2}E_z\Bigr),\\ B_z' = \gamma\!\Bigl(B_z - \frac{v}{c^2}E_y\Bigr). \end{cases} \end{equation}$$其中,洛伦兹因子$\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$,在低速情况下,v<<c,可认为$\gamma \approx 1$。
从这里可得到如下结论:
- 电场和磁场不再彼此独立,当坐标系变换时,不是各自独立地,而是混合地变换;
- 在一惯性系中纯粹是电场或磁场的,在另一惯性系中必定是电场和磁场的混合;
- 不可能将某一惯性系中纯粹的静电场变换到另一惯性系中纯粹的静磁场。
-
动生电动势中的电磁场变换:已知S'系以$\vec{v}=v\hat{i}$相对于S系运动,套变换公式。
-
电场分量:
$$\begin{equation}\begin{aligned}E_x^{\prime}&=E_x=0\\ E_y^{\prime}&=\gamma(E_y-vB_z)=\gamma(0-vB)=-\gamma vB\\ E_z^{\prime}&=\gamma(E_z+vB_y)=\gamma(0+0)=0\end{aligned}\end{equation}$$合电场矢量为$\vec{E}'=-\gamma v B \hat{j}$,低速下近似为$\vec{E}'\approx -v B \hat{j}$。
和公式7不同,在变换后的公式中,v是S系相对于S‘系的速度方向,所以和公式7的符号相反,但在实际上是一致的。 -
磁场分量:
$$\begin{equation}\begin{aligned} B_x^{\prime}&=B_x=0\\ B_y^{\prime}&=\gamma\left(B_y+\frac{v}{c^2}E_z\right)=\gamma(0+0)=0\\ B_z^{\prime}&=\gamma\left(B_z-\frac{v}{c^2}E_y\right)=\gamma(B-0)=\gamma B \end{aligned}\end{equation}$$合磁场矢量为$\vec{B}'=\gamma B \hat{k}$,低速下近似为$\vec{B}'\approx B \hat{k}$。
-
力和电势差:通过变换结果可知,在导体静止参考系(S'系)中,导体内存在一个非静电场$\vec{E}'$驱动电荷运动。
电子受力:$\vec{F}_e=-e\vec{E}^{\prime}=-evB\hat{j}$,沿y轴负方向,和公式6(S系洛伦兹力)一致。
电势差:由于非静电场$\vec{E}'$驱动电荷分离,当系统达到平衡,静电场力要和非静电场力平衡。接下来的公式同式7和8。
-
-
-
感生电动势
任何矢量场都可以分解为涡旋场和势场两部分。
见麦克斯韦方程组(公式9的第2式),法拉第电磁感应:磁场随时间的变化会在空间中激发出电场,称为感生电场。
$$\nabla\times\boldsymbol{E}'=-\frac{\partial\boldsymbol{B}'}{\partial t}$$感生电场就是涡旋电场,涡旋场(或非保守场)的环流不为零,库仑电场是势场,势场的环流为0。
一般地,空间中既有电荷,又有随时间变化(简称时变)的磁场,因此既存在库仑电场,又有感生电场。
$$\begin{equation}\vec{E}\begin{pmatrix}{t}\end{pmatrix}=\vec{E}_{_\text{库}}\begin{pmatrix}{t}\end{pmatrix}+\vec{E}_{_\text{感}}\begin{pmatrix}{t}\end{pmatrix}\end{equation}$$此时,场中任一点电荷q,以速度$\vec{v}$运动,受到的总电磁力(称为洛伦兹力)如下:
$$\begin{equation} \begin{aligned} F&=\text{磁场力}+\text{感应电场力}\\ &=q\vec{v}\times \vec{B}+q\vec{E} \end{aligned} \end{equation}$$首先,由于单位电荷在闭合电路中移动一周时,非静电力做功等于电动势,故感生电场强度$E_{_\text{感}}$沿某一闭合曲线L积分一周,就等于感生电动势:
$$\begin{equation}\oint_L\vec{E}_\text{感 }\cdot\mathrm{d}l=-\frac{\mathrm{d}\Phi}{\mathrm{d}t}\end{equation}$$这里$\Phi$是穿过闭合曲线的磁通量,即以该闭合曲线为边线的曲面S的磁通量:
$$\begin{equation}\Phi=\iint_{S}\textbf{B}\cdot\mathrm{d}\textbf{S}\end{equation}$$注意,磁场穿过闭合回路的量随时间的改变,是产生感生电动势的根本原因;
负号表示感生电动势产生的电流也会激发一个磁场,但激发的磁场和原磁通量方向相反,也就是试图抵消增加的磁通量,这表明稳态系统试图阻碍变化,系统不会无中生有地产生能量。
此外,由于面元dS由两个独立方向(如x和y)构成,因此积分需要覆盖两个参数范围,这是进行二重积分的原因。
故感生电动势的表达式为:
$$\begin{equation} \begin{aligned} \oint_{L}\mathbf{E}_{\text{感}}\cdot\mathrm{d}\mathbf{l}&=-\frac{\mathrm{d}}{\mathrm{d}t}\iint_{S}\textbf{B}\cdot\mathrm{d}\textbf{S}\\ &=-\iint_{s}\frac{\partial \textbf{B}}{\partial t}\cdot\mathrm{d}\textbf{S} \end{aligned} \end{equation}$$总电场产生的电动势满足的公式如下,其中式20.1是来自库仑电场的总电通量:
$$\begin{equation} \begin{aligned}\oint_s\boldsymbol{E}\cdot\mathrm{d}\boldsymbol{S}&=\frac{q_\text{内}}{\varepsilon_0},\\\oint_L\boldsymbol{E}\cdot\mathrm{d}\boldsymbol{l}&=-\iint_s\frac{\partial\boldsymbol{B}}{\partial t}\cdot\mathrm{d}\boldsymbol{S}.\end{aligned} \end{equation}$$两种电动势引出的问题
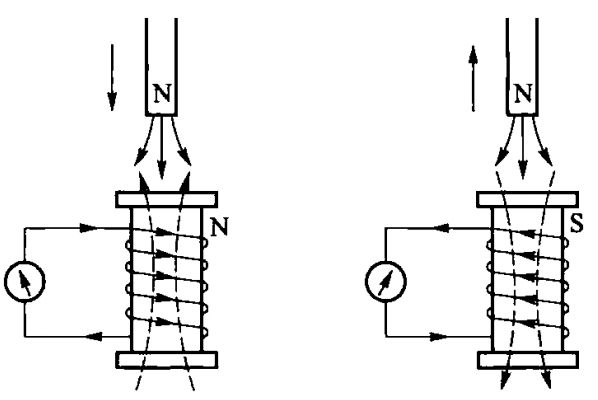
考虑一永磁体和一线圈做相对运动。
对于相对磁铁静止的观察者,线圈中产生动生电动势,源于磁场的洛伦兹力;对于相对线圈静止的观察者,由于磁场的变化,空间中产生涡旋电场,在线圈中诱发感生电动势。
为消除这种不对称性,爱因斯坦建立了狭义相对论,指出把电磁场划分为电场和磁场,和观察者所在的坐标系有关,电磁场作为一个整体,在不同的惯性坐标系中,满足同样的规律。
前文动生电动势部分已经讨论了不同惯性系下的电磁场洛伦兹变换,这里参考前述内容进行论述。
实际上,电场和磁场不是独立的,而是电磁场张量的分量。
$$\begin{equation} \boldsymbol{F}=\begin{vmatrix}0&B_{z}&-B_{y}&-\operatorname{i}\frac{E_{x}}{c}\\\\-B_{z}&0&B_{x}&-\operatorname{i}\frac{E_{y}}{c}\\\\B_{y}&-B_{x}&0&-\operatorname{i}\frac{E_{z}}{c}\\\\\operatorname{i}\frac{E_{x}}{c}&\operatorname{i}\frac{E_{y}}{c}&\operatorname{i}\frac{E_{z}}{c}&0\end{vmatrix} \end{equation}$$这里,前3*3子矩阵包含磁场分量:$F_{12}=B_z\mathrm{,}~F_{13}=-B_y\mathrm{,}~F_{23}=B_x$;
剩下的为电场分量:$F_{0i}=-i\frac{E_i}{c}$,$F_{i0}=i\frac{E_i}{c}$,其中i=1, 2, 3,分别对应x, y, z。
$\textbf{F}$的空间分量(磁场)描述旋转效应,时间-空间分量(电场)描述电荷的推拉效应,二者共同构成电磁场的完整图景。
对于导体棒在磁场中的运动,S系(实验室系)是机械力-洛伦兹力-电荷分离形成电势差;
S'系(导体棒系)需要相对S系进行洛伦兹变换,变换结果为S系中的纯磁场转化为S'系的电场+磁场,在导体棒内部形成非静电场,导致电荷分离,形成电势差;
永磁体-线圈运动主要考虑S'系(线圈静止系),此时永磁体相对线圈运动,导致线圈中的磁场随时间变化,根据法拉第定律,磁场变化在线圈内部产生涡旋电场,这个涡旋电场来驱动电荷运动,形成感生电动势。
需要注意的是,电动势由非静电力产生,与涡旋场有关,与积分路径有关,不能说a、b两点的电动势,只能说ab路径的感应电动势;
电势差是对两点定义的,和积分路径无关,和势场有关。
但是,感应电动势是在导体中维持某种电荷/电流分布的必要条件,因此在导体中,电动势和电势差之间存在一定关系。
磁生电
接下来我们讨论2种情形:
- 对于导体棒在闭合回路中的运动,给闭合回路接上电源,导体棒中流过电流$\vec{I}$,若导体棒长度为L,则载流导体在均匀磁场$\vec{B}$中受安培力$\vec{F}=I\vec{L}\times\vec{B}$,这是磁轨炮(Railgun,
炮姐daisuki)的原理。
注意,导体运动时会切割磁感线,产生反向的动生电动势,但只要电源电压足够高,净效应仍然是导体加速。 - 对于永磁体相对于线圈运动的情形,当线圈通电时,根据安培-麦克斯韦定律,电流和变化的电场(如交流电)都能产生磁场,但当前场景中,导体中电流产生的磁场占主要地位,因此磁场的方向和强度主要取决于电流方向和大小。
若线圈产生的磁场方向与永磁体磁场相反,两者之间产生排斥力,线圈电磁炮(Coilgun)就是利用了通电线圈,产生瞬时的强磁场,对永磁体施加排斥力(可能有时候也会用吸引力,不懂),推动永磁体弹丸沿轴向运动。
需要注意的是,电磁铁跟法拉第电磁感应没关系,因为涡旋电场是磁场变化的结果(或伴随现象),真正激发磁场的是电流或变化的电场。
致谢
本文参考如下资料:
- 知乎用户@西哲7号,专栏文章《感应电动势是如何产生的?》
https://zhuanlan.zhihu.com/p/222052848 - 胡友秋等. 电磁学[M]. 北京: 科学出版社, 2024. ISBN 978-7-03-079527-4.
- 赵凯华,陈熙谋. 电磁学[M]. 第四版. 北京: 高等教育出版社, 2018. ISBN 978-7-04-049971-1.
- 梁灿彬,秦光戎,梁竹健原著;梁灿彬修订. 电磁学[M]. 第四版. 北京: 高等教育出版社, 2018. ISBN 978-7-04-050677-8.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号