可爱的妹子
万能欧几里得
有一条定义域是 \((0,L]\) 的直线 \(l:y=\frac{ax+b}{c}\),有两种操作是 \(P,Q\),一旦 \(l\) 碰到整横线那么执行 \(P\),碰到整竖线则执行 \(Q\),碰到整点默认先执行 \(P\) 再 \(Q\),问直线跑完的结果。
执行 \(k\) 次操作 \(A\) 写作 \(A^k\)。
用一个 \(f(a,b,c,L,P,Q)\) 表示执行这样一个过程,我们想把它化归成更小的问题来做。
先发现将 \(l\) 上下平移整数格是不影响的,于是我们可以把 \(b\) 拉到 \([0,c)\) 这个范围,即 \(f(a,b,c,L,P,Q)=f(a,b\bmod c,c,L,P,Q)\)。
当 \(a\geq c\) 时,发现在碰到一个竖线前必碰到 \(\lfloor\frac{a}{c}\rfloor\) 条横线,将这些个 \(P\) 缩成一个操作,于是有 \(f(a,b,c,L,P,Q)=f(a\bmod c,b,c,L,P,P^{\lfloor\frac{a}{c}\rfloor}Q)\)。
当 \(a<c\) 时,想化成前面的样子,想到交换一下坐标轴。现在考虑交换 \(x,y\) 轴,原坐标系里面定义域是 \((0,L]\),值域是 \((\frac{b}{c},\frac{aL+b}{c}]\),这两个交换,以及 \(P,Q\) 两种操作交换,显然有 \(\frac{b}{c}\in [0,1)\)。
首先若 \(\frac{aL+b}{c}<1\) 那么 \(l\) 不会经过竖线了,而经过 \(L\) 条横线,所以直接执行 \(Q^L\) 并结束。
否则,考虑到原问题的定义域是 \((0,k](k\in N^{+})\) 这样子,为了符合这个形式,再次注意到 \(\frac{b}{c}\in [0,1)\),我们将 \((\frac{b}{c},\frac{aL+b}{c}]\) 从 \(1\) 处截断,再将 \((1,\frac{aL+b}{c}]\) 这部分平移到 \((0,\frac{aL+b}{c}-1]\),最后把后面的分数值截取到整数。还有个小问题即是如果经过整点,那么 \(PQ\) 的顺序会反转,这里做个微扰,将 \(l\) 向下平移 \(\frac{1}{a}\) 即可。于是最终 \(l':y=\frac{cx+c-b-1}{a}\)后半部分化为以 \(f(c,c-b-1,a,\lfloor\frac{aL+b}{c}\rfloor-1,Q,P)\) 解决。
最后我们要处理 \((\frac{b}{c},1]\),\((\lfloor\frac{aL+b}{c}\rfloor,\frac{aL+b}{c}]\) 这两个边界定义域。对于首段,交且仅交一个竖线 \(x=1\),交 \(\lfloor\frac{c-b}{a}\rfloor\) 个横线,但是注意到中间那部分下移 \(\frac{1}{a}\) 的操作,假如 \(\frac{c-b}{a}\) 是个整数那么会被那边的多统计一次,所以我们不妨也直接把这个和中间对齐,就是 \(\lfloor\frac{c-b-1}{a}\rfloor\) 条横线。
再看尾段,这里显然不会再经过竖线了,令 \(t=\lfloor\frac{aL+b}{c}\rfloor\) 和上面同理,横线会经过 \(L-\lfloor\frac{ct-b-1}{a}\rfloor\) 条。
发现这个有点像三个数的欧几里得,如果做操作的代价是 \(O(t)\) 的,那么总复杂度 \(O(t\log V)\)。
如果题里面的定义域包括 \(0\),那么要在 \(0\) 处向上跑截距条横线再向右跑一格再进行。
把一个减的直线换成增的扔到原点上且整点数不变:\(l:y=\frac{-ax+b}{c}\rightarrow l':y=\frac{ax-b\bmod a}{c}\)。
lg 模板的代码:
点击查看代码
# include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ldb;
const ll Mod = 998244353;
struct Element{
ll s , u , r , ss , zs , si;
Element operator + ( Element y ) {
Element ret = { 0 , 0 , 0 , 0 , 0 , 0 };
ret . u = ( u + y . u ) % Mod , ret . r = ( r + y . r ) % Mod;
ret . s = ( s + y . s + ( u * y . r % Mod ) ) % Mod;
ret . ss = ( ss + y . ss + ( 2 * u * y . s % Mod ) + ( u * u % Mod * y . r % Mod ) ) % Mod;
ret . si = ( si + y . si + r * y . r % Mod ) % Mod;
ret . zs = ( zs + y . zs + ( u * y . si % Mod ) + ( u * r % Mod * y . r % Mod ) + ( r * y . s ) % Mod ) % Mod;
return ret;
}
};
Element Quick_Pow( Element u , ll k ){
Element ret = { 0 , 0 , 0 , 0 , 0 , 0 };
while( k ){
if( k & 1 ) ret = ret + u;
u = u + u , k >>= 1;
}
return ret;
}
Element Solve( ll a , ll b , ll c , ll L , Element P , Element Q ){
if( ! L ) return ( Element ){ 0 , 0 , 0 , 0 , 0 , 0 };
b %= c;
if( a >= c ) return Solve( a % c , b , c , L , P , Quick_Pow( P , a / c ) + Q );
ll t = ( a * L + b ) / c;
if( ! t ) return Quick_Pow( Q , L );
ll k = L - ( c * t - b - 1 ) / a , d = ( c - b - 1 ) / a;
return Quick_Pow( Q , d ) + P + Solve( c , c - b - 1 , a , t - 1 , Q , P ) + Quick_Pow( Q , k );
}
int main(){
ll T;
scanf( "%lld" , & T );
while( T -- ){
ll L , a , b , c;
scanf( "%lld%lld%lld%lld" , & L , & a , & b , & c );
Element _P = { 0 , 1 , 0 , 0 , 0 , 0 } , _Q = { 0 , 0 , 1 , 0 , 0 , 0 };
Element ans = Quick_Pow( _P , b / c ) + _Q + Solve( a , b , c , L , _P , _Q );
printf( "%lld %lld %lld\n" , ans . s , ans . ss , ans . zs );
}
return 0;
}
\(\bold{Miller-Rabin}\)
\(\text{Fermat}\) 小定理:
二次探测定理:
虽然它们都非 \(p\) 为素数的充分条件,但是我们可以多随机一些 \(x\) 来检测来保证很高的正确率。
考虑先分解为 \(p=2^{k}q+1\),然后对随机出的 \(x\) 算出 \(x^{q}\),然后不断平方算 \(x^{2q},x^{4q},\cdots,x^{p-1}\),如果中间出现了一个非 \(1\) 和 \(p-1\) 数那么测试失败,否则 \(p\) 大概率是个素数。
做 \(k\) 轮测试的时间复杂度是 \(O(k\log p)\) 的,如果你认为做乘法是 \(O(1)\)。失败率是 \(4^{-k}\)。
听说有什么的基于广义 \(\text{Riemann}\) 猜想的确定性判素只需要测 \(1,2,\cdots,\lfloor 2\ln^2 n\rfloor\),然后有这几个底数能判 \(2^{64}\):\(2,325,9375,28178,450775,9780504,1795265022\)。
杜教筛
求数论函数 \(f\) 在某处的前缀和 \(F(n)=\sum_{i=1}^n f(i)\)。为此我们需要凑出两个容易求前缀和的 \(g,s\) 满足 \(f*g=s\),不依赖你积性与否。
那么有
一般有 \(g(1)=1\),再在两边求和得
于是就可以愉快数论分快然后递归做,复杂度是 \(T(n)=\sum_{i=2}^{\sqrt n}T(\lfloor\frac{n}{i}\rfloor)+O(\sqrt n)=O(n^{\frac{3}{4}})\) 的。如果线性筛预处理掉前 \(O(n^{\frac{2}{3}})\) 的话就是 \(O(n^{\frac{2}{3}})\) 的。
dp x 计数
决策单调性
是说一些 \(\text{DP}\) 上决策点单调的事情,有四边形不等式啥的但也不是必要条件,总之看起来像就好。
可以分治转移,要求这个 dp 是层与层之间的转移,层内没有转移,两层之间可以用一次分治来解决。考虑分治当前范围 \([l,r]\),它的决策点范围是 \([L,R]\),选一个中点 \(m\),找它的决策点 \(p\),那么 \([l,m-1]\) 的决策点范围就是 \([L,p]\),右边同理决策点只能在右边,这就能分治了。
转移 \(k\) 层复杂度 \(O(nk\log n)\)。
另外在上面跑莫队指针移动量是 \(O(n\log n)\) 的。
也可以单调队列转移,还需要一个二分来查,这个好像叫做“二分队列”,具体地,我们维护一个决策点的队列,上面有这个决策点目前(之所以这么说是因为后面新来的可能会比他更左)能控制到的最左的地方。
当要转移的时候,先弹队头直到当前队头控制的地方包含这个位置,然后按照队头转移,再把这个新点加到队列里,具体地,我们对队尾和这个点二分来找到最左边的新点比队尾更优的地方,假如这个地方比队尾原本能控制的最左地方还左,那么队尾没用了直接 \(\text{pop}\) 掉,直到不满足这个条件我们把新点塞进队尾。
这个东西能用在一层里面互相转移。前面那个分治不行。
显然一次二分会弹掉一个队里面的元素,队里面总元素数量 \(O(n)\),那么总时间复杂度是 \(O(n\log n)\) 的。
再就设这个 \(g_{i,j}\) 表示二维上这个地方的决策点下标,那么有
这个牛逼,如果我们按照这个范围暴力枚举,总枚举的规模是 \(O(n^2)\) 的。大概就是我们把所有 \((i,j)\),\((i+1,j+1)\) 这些斜线标出来,我们就是在某种顺序遍历这些斜线,那么规模就是 \(O(n^2)\) 的了。
还有一个东西是路径交错,就是分 \(k\) 段问题,\(k+1\) 段形成的这些段点一定交错在 \(k\) 段形成的地方,差不多是这样
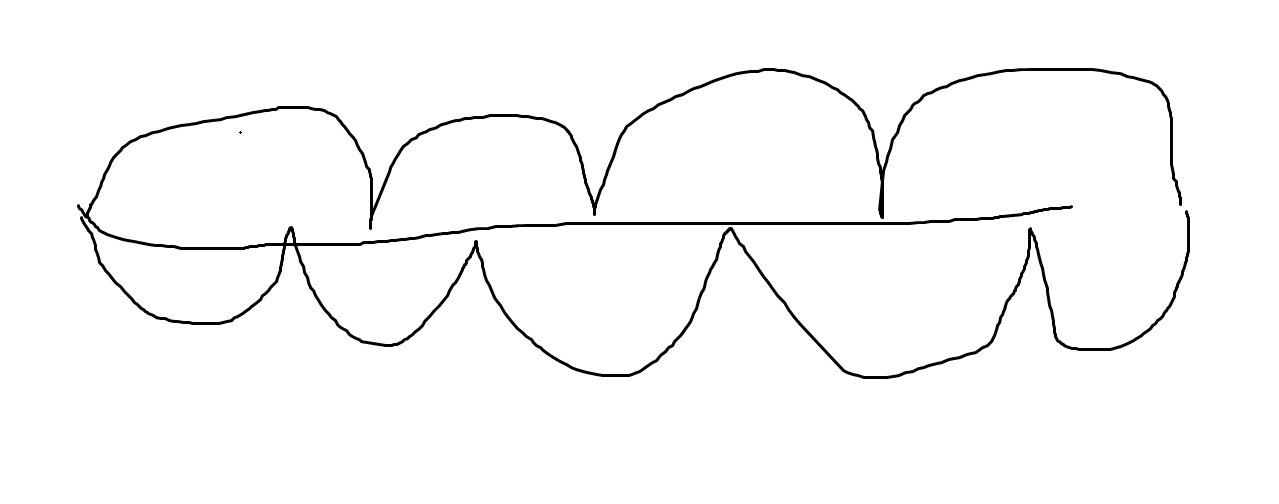
例题 CF833B The Bakery,P5574 [CmdOI2019]任务分配问题 CF321E Ciel and Gondolas P6246 [IOI2000] 邮局 加强版
P3515 [POI2011] Lightning Conductor
wqs 二分
有些时候问题能够抽象成恰好选 \(k\) 个物品最大化收益的问题,并且令 \(f(x)\) 表示选 \(x\) 个时候的最大收益,\(\Delta f(x)=f(x)-f(x-1)\) 是单调减的,就是说物品拿的越多获得的额外收益是变小的,于是 \((i,f(i))\) 形成一个凸壳,我们要求的就是 \((k,f(k))\) 这个点的横坐标。另外就是我们还需要能快速地求出没有 \(k\) 的限制的时候问题的答案。
但是我们是不知道这个凸壳长什么样子的只知道他是个凸壳,wqs 二分的做法是:凸包上斜率是单调的于是二分斜率 \(c\) 并获取它与凸包的切点,并向 \(k\) 的地方调整,直到与凸包相切与 \((k,f(k))\),得到答案。具体来说,凸包切线是 \(f(x)=cx+b\) 其中 \(b\) 是截距,我们想要找到切点实际上就是截距最大的点,即让 \(b=f(x)-cx\) 最大,我们惊喜地发现这个实际上就是每个物品的收益减去 \(c\) 后的不限制 \(k\) 的原问题,我们能在 \(O(T(n))\) 中求出它的最优解获得此时选几个就得到了当前切点的横坐标。于是就能继续二分,在 \(O(T(n)\log V)\) 的时间里面解决这个问题。
例题 P5633 最小度限制生成树 P6246 [IOI2000] 邮局 加强版 P2619 [国家集训队2] Tree I
容斥
作用是把 “恰好” 转成 “至少/至少存在多少个”
静电容斥是一些条件 \(U=\{p_1,p_2,\cdots,p_m\}\) 和一些需要计数的满足或不满足一些条件的元素,\(f(S)\) 表示至少满足 \(S\) 中所有条件的元素数量,那么所有条件都不满足的元素数量是
而至少满足一个限制的元素数量是
二项式反演
是熔池,沟通一些函数的反演关系,比较牛逼
\(f_k\) 表示恰好满足 \(k\) 个条件,\(g_k\) 表示至多满足 \(k\) 个条件那么
\(g_k\) 表示至少满足 \(k\) 个条件那么
二维二项式反演
反方向的懒得写了,和上面那个类似的
dp 里面维护容斥的式子,因为乘法分配律的原因,是比较直观的。
d3t1 another solution by 2019zll
\(f(S)\) 表示钦定 \(S\) 里面的位置是坏段结尾,其他的随便的方案数,当然这个 \(S\) 要合法。
考虑容斥,dp 维护它,就是 \(f_i\) 表示最靠后一次钦定是 \([i-2k+1,i-k],[i-k+1,i]\) 是坏段的 \(S\) 对答案的贡献。转移是
答案是 \(\sum_{i=0}^n f_i\)。
noip10t1
\(f(S)\) 表示钦定 \(S\) 里面的位置不合法,其他位置随便的方案数,是说 dp 一个 \(f_i\) 表示维护到 \(i\) 的答案,注意到这个条件说明 \(a_{i+1}\leq\frac{a_i}{2}\),那么不合法连续段的长度是 \(\log\) 级别的,转移的时候直接枚举最后一个不合法连续段的长度转移即
其中 \(g_k\) 表示长为 \(k\) 的不合法段数量,这个可以预处理,就能 \(O(n\log n)\) 做了。
[JSOI2011] 分特产
令 \(f_i\) 表示至少有 \(i\) 个人没分到特产,那么我们知道答案是 \(\sum_{i=0}^n(-1)^i f_i\),看看怎么算 \(f_i\):枚举剩下的 \(n-i\) 个人,对于一个物品 \(i\),相当于 \(c_i\) 个无标号小球放入 \(n-i\) 个有标号盒子,插板即可:
[CTS2019] 随机立方体
首先反演一下,令 \(t=\min\{n,m,l\}\)
\(f_k\) 表示钦定存在 \(k\) 个极大数其他的不管方案数。现在考察这个,可以分为两部分:极大数和被他影响的数 \(p\),剩下的数 \(q\)。
看到一个极大数会影响到三个经过他的平面,那么 \(g(x)=(n-x)(m-x)(l-x)\) 表示填了 \(x\) 个极大数剩下的格子,\(G(x)=nml-g(x)\) 表示这些被影响的格子。
先考虑 \(q\),先把他们选出来要填什么是 \(\binom{nml}{g(k)}\),不同方案数量是 \(g(k)!\),故 \(q=\binom{nml}{g(k)}(g(k)!)\)。
再考虑 \(p\),先把它们的位置确定下来,它们不能共面所以是 \(s=\prod_{i=0}^{k-1}g(i)\),考虑到任意两个极大数影响的平面们会有交,我们就想到给它们钦定一个顺序来避免复杂的讨论,就是从小往大填极大值,假如现在填了 \(k-1\) 个极大值且都比当前要加入的极大值小,那么这个极大值加进去后影响的平面会和之前填的数字有交,但是,这不影响,因为我们从小往大填极大值,这些数字比之前填的极大值要小,自然也比当前这个极大值小。设一个 \(p_k\),然后考虑往 \(p_{k+1}\) 怎么算,这会新增 \(G(k+1)-G(k)\) 个格子,有一个格子要填极大值,剩下的 \(G(k+1)-G(k)-1\) 个格子里面的数字任意排列,还要分配一下数字即 \(G(k+1)-1\) 个数哪些分给上一拨哪些分给当前新增的,所以就是 \(G(k+1)-1\) 个数选出 \(G(k+1)-G(k)-1\) 个任意排列,其他的分给上一拨来分配,即 \(p_{k+1}=(G(k+1)-1)^{\underline{G(k+1)-G(k)-1}}p_k=\frac{(G(k+1)-1)!}{G(k)!}p_k\),也即 \(p_k=\prod_{i=0}^{k-1}\frac{1}{G(i)!}\prod_{i=1}^k (G(i)-1)!\)。最后 \(p=sp_k\)。
组合起来就得到
非常简洁的式子,线性处理 \(G(i)\) 的逆元再反演就能做到 \(O(Tn)\) 了。
上下界
无源汇上下界可行流:给每个边强制流 \(\text{min}\),取残量网络,再看这个网络上有什么点是不满足流量守恒的,建个源汇 \(S,T\),设 \(u\) 的 \(\mathrm{in}-\mathrm{out}=k\),则连
然后我们用 \(S,T\) 跑 \(\text{maxflow}\),如果从 \(S\) 流出的边全部满流即 \(\text{maxflow}=\sum k[k>0]\) 说明是可行的,感性理解一下就能明白。
有源汇可行:连一个 \((T,S,+\infty)\) 就变成无源汇了。
something
https://www.luogu.com.cn/blog/xht37/er-fen-tu-yu-wang-lao-liu
https://www.luogu.com.cn/blog/Link-Cut-Treeeee/qian-tan-wang-lao-liu-jian-mu-di-ji-ji-yin-qiao
https://www.luogu.com.cn/blog/command-block/mu-ni-fei-yong-liu-xiao-ji
graph
圆方树很有用
把原图做点双,每个点双新建一个方点,连在它其中的所有的点作为圆点,形成一棵树。
P8456 「SWTR-8」地地铁铁
我们考虑用总数减去不合法的,分为三种:之间只有白路径,只有黑路径,有白路径有黑路径但是两者之间没有交。
现在考虑说先处理前面两种情况,是对称的。把圆方树建出来,统计一下纯白连通块,每个连通块里面的点对之间都有一个贡献。
下面是说,如果是第三种情况,那么这两个点一定在一个点双中。证明也很简单,是说假如不在一个点双里面那么所有路径一定交在一个割点上,黑白路径也必定会有交了。
再者,一个点双内部只会有一对这样的点对,不然假设有一个 \(w\) 满足旁边连了一条黑边一条白边,因为强联通性我们总能找到 \((u,v)\) 过这两条边的路径,交在 \(w\) 上且颜色还不一样。
时间复杂度 \(O(n+m)\)。
[2020-2021 集训队作业] Tom & Jerry
感性理解一下如果这个图的连通性很强那么 jerry 总是能到处跑的,那么我们先把圆方树建出来,tom 需要走割点将 jerry 所在的子树越拉越小。是说必须走割点,不然 jerry 总能在整张图上到处跑。
在圆方树上这个是好看的,那么在圆方树上 tom 能从一个圆点跳过方点走到一个圆点,必须是这两个圆点在原图也相邻。
那么我们说点对 \((u,v)\) 是好的当且仅当圆方树上 \((u,v)\) 路径中的相邻圆点在原图也相邻。tom 的胜利条件就能表述为删掉 \(b\) 后对于所有在 \(a\) 所在的联通块的点 \(u\),都有 \((b,u)\) 是好的,这个是容易理解的。或者说另存在一个点 \(v\) 满足对于所有 \(w\in V\) 都有 \((v,w)\) 是好的那么 tom 也能赢,只要先跑到那里即可。
所以我们做一个换根 \(\text{DP}\) \(f_u\) 表示自己对自己子树中的所有点是不是都是好的,如果是方点那么就是自己的父亲到自己子树中所有点是不是好的。那么当 \(u\) 是圆点的时候 \(f_u=\mathrm{and}_{v\in s(u)} f_v\),否则 \(f_u=[(\mathrm{fa}_u,u\text{ is good})]\mathrm{and}_{v\in s(u)} f_v\)。\(g_u\) 表示父亲子树,能从根开始往下推地拼起来算。
假如存在一个圆点 \(u\) 满足 \(f_u=g_u=1\) 那么 tom 总能赢。不然就定位一下 \(a\) 在 \(b\) 的那颗子树,判断 \(f_b/g_b\) 的值即可。
时间复杂度 \(O(n\log n)\)。
data structure
[SDOI2018] 物理实验
我们想一个 \(x\) 轴上的单位格的权值是从它出去能射到的线段长度,扫描线扫 \(x\) 轴,我们只要知道当前离 \(x\) 轴最近的线段是谁就好了。这个可以用一个 \(\text{set}\) 维护,具体就是存一些一次函数 \(f(x)\),按照当前扫到 \(x\) 轴的位置 \(x'\) 的 \(f(x')\) 来排序,因为线段之间没交,所以只有插入删除的时候顺序有改变。最后找一个权值最大的 \(L\) 区间就好了。
精度和旋转坐标什么的好恶心
CF704E Iron Man
首先假设是一条链的情况,我们建一个系表示这些点的运动情况,\(x\) 轴表示时间 \(y\) 轴表示位置,当然这个是按照 \(\text{DFS}\) 序排的,那么每个点的运动都能表示成一个线段,需要找第一个线段交点,我们考虑扫 \(x\) 轴,依次加入线段,发现加入一个线段的时候要找的交点只能是这个线段和 \(y\) 轴上离他最近的线段的交点,否则是说会和第一个这个条件矛盾。所以我们上面的方式维护这些线段就好。
上树,就是树链剖分,就能转化成链上的情况,每个动点被算 \(O(\log n)\) 次,总时间复杂度两个 \(\log\)。
[Ynoi2010] Self Adjusting Top Tree
[Ynoi2016] 镜中的昆虫
先考虑说是单点的修改,区间数颜色可以转化成 \((i,\mathrm{pre}_i)\) 的二维数点,有一个 \(a_p\rightarrow a_p'\) 的修改,那么变化 \(\mathrm{pre}\) 值的地方会有它本身和后面第一个与 \(a_p\) 同色的,第一个和 \(a_p'\) 同色的这三个地方。于是我们对每个颜色开一个 \(\text{set}\) 存它的所有出现位置就能定位到,因此一次修改是需要改 \(O(1)\) 个点。
此时需要解决带修二维数点,考虑 \(\text{CDQ}\) 分治(我也不很会 \(\text{CDQ}\)!!!)的话,分治掉时间这一维度,是说前面的修改会对后面的询问有贡献,如果分治到 \([l,r]\) 这段时间,中点 \(m\),两边的东西可以分治,只需考虑跨过两边的事情,这个就是 \([l,m]\) 里面的修改对 \([m+1,r]\) 有贡献,我们把 \([l,m]\) 这里面的修改先全部砸到 \([m+1,r]\) 里面去,就是一个先进行所有修改再进行所有询问的静态问题,离线一维然后扫描线就行啦qwq。
此时分治 \(O(\log q)\) 层,一层里面 \(O(q\log n)\),总复杂度两只 \(\log\)。
如果是区间推平,结论是 \(\mathrm{pre}\) 单点改变的数量级是 \(O(n+q)\) 的。证明不很懂qwq。感受一下就是推平会让中间的那些都变成 \(\mathrm{pre}_i=i-1\) 这样,再推平也只会导致左端点和整个颜色和之前的颜色在右边的一个点的 \(\mathrm{pre}\) 变化这样。
可以考虑用 \(\text{set}\) 维护颜色段维护整个序列,再对每个颜色开个 \(\text{set}\) 维护它的颜色段,就能比较方便地算 \(\text{pre}\) 的变化了,算完变化就和询问什么的一块塞进 \(\text{CDQ}\) 里面跑就好了。
时间复杂度 \(O(n\log^2 n)\),线性空间。
d3t2 rdexq
\(\text{range division equal x query}\)
\(O(n\sqrt n\log n)\):离线把询问挂到左端点上,从 \(n\) 到 \(1\) 倒着扫,设当前扫到 \(t\),维护一个数组 \(p_x\) 表示满足 \(\lfloor\frac{a_i}{a_j}\rfloor=x\),\(t\leq i\leq j\) 的最小的 \(j\),询问的时候只需要查是否有 \(p_x\leq r\) 即可。
维护只需对 \(a_i\) 数论分快,分块到 \([l,r]\) 的时候就查值域 \([l,r]\) 里面最小的下标,用这个更新 \(p_x\) 即可。复杂度是 \(O(n\sqrt n\log n)\)。用 zkw 卡常就能过啦
void Modify( int p , int x ){
T[ p += L ] = x;
for( p >>= 1 ; p ; p >>= 1 ) T[ p ] = min( T[ p << 1 ] , T[ p << 1 | 1 ] );
}
int Query( int l , int r ){
int ret = Inf;
l += L - 1 , r += L + 1;
while( l ^ r ^ 1 ){
if( ~ l & 1 ) ret = min( ret , T[ l ^ 1 ] );
if( r & 1 ) ret = min( ret , T[ r ^ 1 ] );
l >>= 1 , r >>= 1;
}
return ret;
}
for( L = 1 ; L <= V + 1 ; L <<= 1 );
for( int i = 0 ; i <= L + V + 1 ; i ++ ) T[ i ] = Inf;
d6t1
设 \(f_{i,k}\) 表示考虑 \(a_1,\cdots,a_i\) 且 \(a_i=0\),\([1,i-1]\) 中有 \(k\) 个区间为全为 \(1\) 的方案数,那么有转移 \(f_{i,k}=\sum_{j=1}^{i-1}f_{j,k-g(j+1,i-1)}\),其中 \(g(j+1,i-1)\) 表示 \([j+1,i-1]\) 中完整区间个数。那么我们发现 \(f_i\) 这个数组实际上是由 \(f_1,f_2,\cdots,f_{i-1}\) 每个都平移一下然后按位加起来的结果,那么加入一个完整的区间 \([l,r]\) 就会将 \(f_1,f_2,\cdots,f_{l-1}\) 向右平移一位,于是我们在线段树上每个节点开一个长为 \(m\) 的数组维护区间内所有 \(f_i\) 的按位和,打标记平移数组,就是 \(O(nm\log n)\) 的了。
[PA2014] Druzyny
限制肯定是取那些最紧的,令 \(L(l,r)=\max_{i=l}^r\{c_i\},R(l,r)=\min_{i=l}^r\{d_i\}\) 首先一个朴素的 dp 是 \(f_i=\max_{0\leq j< i,i-j\in[L(j+1,i),R(j+1,i)]}\{f_j\}+1\),手搓一些之后发现这些合法点没什么规律也不很连续,考虑 cdq 分治一下,中点是 \(m\),考察一个 \(j\) 转移到 \(i\),我们把限制分成两段:\(i-j\in[L(i,mid),R(i,mid)],i-j\in[L(mid+1,j),R(mid+1,j)]\),我们从 \(mid\) 往右扫 \(i\),期间实时维护一棵下标线段树存所有满足限制 1 的 \(j\) 的 dp 值,那么只需询问第二个限制的区间 \(\max\) 即可,就是 \(L(mid+1,j)\leq i-j\leq R(mid+1,j)\Leftrightarrow i-R(mid+1,j)\leq j\leq i-L(mid+1,j)\) 这样。那么如何维护这颗线段树呢?我们考虑到钉住一个 \(j\),右移 \(i\),看限制 1 下的满足情况变化,那么显然当 \(i-j=L(i,mid)\) 时 \(j\) 开始可以转移,当 \(i-j=R(i,mid)+1\) 时停止,这是对于一个 \(j\) 的一段合法 \(i\) 的区间,因此我们开很多 vector,对这个区间两个端点挂上 \(j\),扫 \(i\) 的时候加入删除即可。时间复杂度 \(O(n\log^2 n)\)。
acm,每日,杂题
CF1333E Road to 1600
SB 题,赛时一直在想构造一些八皇后问题的东西,然后寄了。没想到这么 SB,我们能够暴搜到 \(n\leq 2\) 没有解,\(n=3\) 有一组解,是这个
然后我们考虑是把 \(n>3\) 的情况诱导到这个上面来,具体地说就是把这个放在左上角并值域集体往上平移到顶,我们再在它的右下螺旋包裹它就构造完了。
CF1394C Boboniu and String
tourist sniper 因为 tourist 这题赛时 FST 了下了很多分。
首先把一个字符串看成坐标系里面一个点 \((b_i,n_i)\) 分别表示 \(s_i\) 里面 \(B\) 和 \(N\) 的数量,那么这些操作就表示这个点能在坐标系上下左右以及左下右上对角线移动,这时 \(\mathrm{dist}(s_i,s_j)=\)
那么,这是一个坐标系上的单峰函数,我们退火拿下。
麻蛋的卡了好久才卡出来,有 mt19937 用法:
mt19937 gen( time( 0 ) );
db Rand( db l , db r ){
uniform_real_distribution< ( 这里面填数据类型 qwq ) >dis( l , r );
return dis( gen );
}
[POI 2019] Układ scalony
首先看 \(nm\) 是奇数的情况,考虑这个直径放在哪里是这样
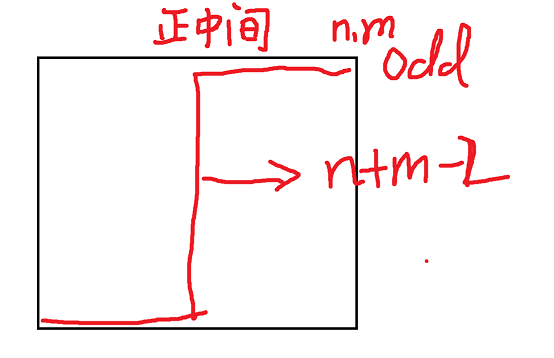
感性理解一下就知道直径长度界是 \([n+m-2,nm-1]\),如果这个直径要延长就向旁边蛇形延
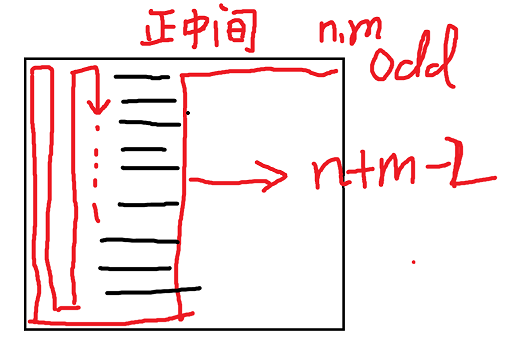
然后如果 \(n,m\) 有一个是偶数,我们依然能像上面一样构造。
然而如果 \(n,m\) 全是偶数,就发现找不到一个最中间的线了,必然会往哪边偏一点,这个直径就有可能不太够,这就导致此时直径长度界是 \([n+m-1,nm-1]\),构造如上。
\(n,m\) 里面有 \(2\) 的时候要特殊做,因为两边找不到空。。。
d5t3 / [BalticOI 2022 Day1] Uplifting Excursion
观察到 \(W\leq 10^{18}\) 而 \(w_i\leq 400,c_i\leq 10^12\),这个背包的大小很大而物品却都很小,就想到先按照 \(\frac{v_i}{w_i}\) 优先填这些性价比高的物品直到背包将要满而塞不动了,然后再对最后的边界进行调整。设 \(\max\{w_i\}=k\) 注意此时的 \(|W-\sum w_i|<k\)。
考虑这个调整的过程,是会删掉一些物品,加入一些物品,首先通过调整这些操作的顺序,我们可以保证任何时刻 \(|W-\sum w_i|<k\),并且调整过程中,\(\sum w_i\) 不会达到同一个位置,这样一定不优或者不必要,所以我们至多调整 \(2k\) 个物品,不管顺序的话调整的值域是 \(O(k^2)\) 的,所以我们直接多重背包,先跑一遍加物品,再把体积取相反数跑一遍当去掉物品,就做完了。复杂度 \(O(n w_i^2\log a_i)\)(二进制分组)。
CF364D Ghd
假如我们知道某个数 \(x\) 存在于答案集合中,那么我们可以算出所有可能成为 ghd 的数,具体的就是 \(\gcd(x,a_i)\),容易发现这些数的数量不超过 \(d(x)\),然后我们 \(O(d^2(x))\) 地计算出这些数互相整除的情况就知道有没有数整除超过一半的原数列,进而统计答案。然而我们知道答案集合大小 \(\geq\frac{n}{2}\),所以我们随机一个 \(a_i\) 不在这个集合里面的概率是 \(\frac{1}{2}\),随机 \(k\) 次的错误率是 \(\frac{1}{2^k}\),大概取 \(k=12\) 左右就能过了。
时间复杂度 \(O(kn\log nd^2(V))\)。
「TAOI-2」Ciallo~(∠・ω< )⌒★
二次元儿
首先分成两种情况: \(s\) 中本来就有 \(t\) 和 \(s\) 劈开之后缝合出一个 \(t\)。第一种情况平凡,直接看第二种情况。
考虑对 \(s\) 预处理一个 \(f_i\) 表示从 \(s_i\) 往后和 \(t\) 的最长公共前缀的长度,\(g_i\) 表示从 \(s_i\) 往前和 \(t\) 的最长公共后缀的长度。然后扫 \(f_i\),查后面有多少 \(g_j\) 会对他产贡献,不难发现需要 \(g_j\geq |t|-f_i\) 否则凑不齐一个 \(t\),并且由于中间至少要劈掉一点,需要 \(i-|t|\leq j\) 否则前后缀会重合或者恰好接上,如果都合法那么一对前后缀公共部分可以随便从中间切开,故贡献是 \(f_i+g_j-|t|+1\)。
整理一下条件发现这是二维偏序,下标一维自动排序了,另外一维树状数组即可。至于预处理不是瓶颈,可以用带 \(\log\) 的二分/倍增哈希或者 exkmp(虽然我不会),总时间复杂度 \(O(n\log n)\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号