计算理论 (一):有穷状态机与正则语言
自动机理论是计算理论中的一个重要的分支,其致力于建立抽象的计算模型来阐释计算,用抽象刻画出来的 “计算机” 来解决一些问题,在不同的领域都有作用,比如形式语言或者可判定性,可计算性等。而 有穷状态机 \(\text{(finite state machine)}\) 是一类最基础,最简单的计算模型。
语言与短语结构文法
定义 字母表 为任意一个非空有穷集合,用 \(\Sigma\) 表示,其中的元素为字母表中的符号,而 字母表上的字符串 为该字母表中符号的有穷序列,字符串的集合则称为 语言。
例如设 \(\Sigma_1=\{0,1\}\),则 \(01001\) 为 \(\Sigma_1\) 上的一个字符串,而 \(\{\varepsilon,0,1,0001,10\}\) 为 \(\Sigma_1\) 上的一个语言。其中 \(\varepsilon\) 表示空串,即长度为 \(0\) 的字符串。
文法 用来描述语言,在一个短语结构文法的字母表上有 终结符 和 变元 两种符号,包含变元的一个字符串可以用另一些符号来替换,而文法的 产生式 则用来描述这种替换规则,指明 \(z_0\) 可以替换为 \(z_1\) 的产生式记为 \(z_0\rightarrow z_1\)。一个文法中有一个 起始变元 \(S\),我们总是从起始变元开始定义其它字符串。
一个文法可以生成若干字符串,其方式是通过起始变元,根据产生式将字符串中的某部分替换为产生式右边的字符串,直到字符串中没有变元为止。获取一个字符串的替换序列称为 派生。
如令终结符为 \(0,1,\text{q},\text{w}\),有两个产生式
它产生 \(00\text{qwq}11\) 的派生过程为
下面我们形式化地定义短语结构文法以及它产生的语言:
一个 「短语结构文法」 是一个四元组 \(G=(V,\Sigma,R,S)\),其中
$1.\ $ \(V\) 是一个有穷集合,称为 变元集。
$2.\ $ \(\Sigma\) 是一个与 \(V\) 不相交的有穷集合,称为 终结符集合。
$3.\ $ \(R\) 是一个有穷 产生式集,每一个产生式左边必须至少包含一个变元。
$4.\ $ \(S\in V\) 是 起始变元。
设 \(u,v,z_0,z_1\) 是由变元和终结符组成的字符串,\(z_0\rightarrow z_1\) 是文法的一条规则,那么称 \(uz_0v\) 生成 \(uz_1v\),记作 \(uz_0v\Rightarrow uz_1v\)。如果 \(u=v\) 或存在序列 \(u_1,u_2,\cdots,u_k(k\geq 0)\) 使得
则称 \(u\) 派生 \(v\),记作 \(u\stackrel{*}{\Rightarrow} v\)。
由 \(G\) 生成的语言 \(L(G)\) 是起始变元能派生的所有仅由终结符组成的字符串,即
根据产生式的类型,短语结构文法被分为四类:
\(0\) 型 文法:产生式没有限制。
\(1\) 型 文法:有两种产生式,一种是 \(w_1\rightarrow w_2\),其中 \(w_1=uAv\),\(w_2=uwv\),\(A\) 是一个变元,\(u,v\) 是由变元或终结符组成的串,\(w\) 是变元或终结符构成的非空串。一种是 \(S\rightarrow\varepsilon\)。\(S\) 不能出现在产生式的右边。
\(2\) 型 文法:只有一种产生式 \(A\rightarrow w\),其中 \(A\) 是一个变元,\(w\) 是由变元或终结符构成的串。
\(3\) 型 文法:产生式为 \(A\rightarrow a\) 或 \(A\rightarrow aB\) 或 \(S\rightarrow\varepsilon\) 其中 \(a\) 是终结符,\(A,B\) 是变元。
其中 \(1\) 型文法称为 上下文有关文法,\(2\) 型文法称为 上下文无关文法,\(3\) 型文法称为 正则文法。
有穷状态机
有穷状态机也可以叫做有穷自动机,因为习惯下文中将用 “自动机” 来代指这类对象,具体分类依据上下文而定。
下图描述了一个有穷状态机 \(\mathrm{M}\):
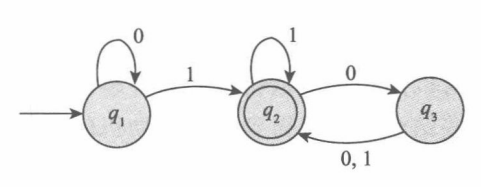
该图称为 \(\mathrm{M}\) 的 状态图,它有 \(3\) 个状态 \(q_1,q_2,q_3\),其中中 起始状态 \(q_1\) 用一个指向它的无出发点的箭头表示,接受状态 \(q_3\) 用双圈表示。状态之间用称为 转移 的箭头联系起来。
自动机以字符串为输入,它处理输入字符串并产生一个输出,表示为 接受 或 拒绝。它从左往右逐个接受输入字符串的所有符号,当输入一个符号时,它将沿着标有该符号的转移从一个状态移动到另一个状态,当输入最后一个符号时产生输出,如果自动机处于一个接受状态,输出为接受,否则为拒绝。
顺便一提,上图中的自动机接受所有至少含有一个 \(1\) 且在最后一个 \(1\) 后有偶数个 \(0\) 的字符串。
接下来我们将形式化地定义有穷自动机和在它上面的计算:
「有穷状态机」 是一个五元组 \(\mathrm{M}=(Q,\Sigma,\delta,q_0,F)\),其中
$1.\ $ \(Q\) 是一个有穷集合,称为 状态集。
$2.\ $ \(\Sigma\) 是一个有穷集合,称为 字母表。
$3.\ $ \(\delta:Q\times\Sigma\rightarrow Q\) 是 转移函数。
$4.\ $ \(q_0\in Q\) 是 起始状态。
$5.\ $ \(F\subseteq\) 是 接受状态集。
设 \(w=w_1w_2\cdots w_n\) 是一个字符串,如果存在 \(Q\) 中的状态序列 \(r_1,r_2,\cdots,r_n\) 满足下述条件:
$1.\ $ \(r_0=q_0\)
$2.\ $ \(\delta(r_i,w_{i+1})=r_{i+1}\) 对于 \(i=0,1,\cdots,n-1\)
$3.\ $ \(r_n\in F\)
则称 \(\mathrm{M}\) 接受 \(w\)。
称自动机 \(\mathrm{M}\) 接受的全部字符串集合 \(L\) 为 自动机 \(\mathrm{M}\) 的语言,或者说 \(\mathrm{M}\) 识别 \(L\),记为 \(L(\mathrm{M})\)。对于一个自动机 \(\mathrm{M}\),这个 \(L\) 是唯一的。
例如前面图中的 \(\mathrm{M}\) 可以形式地写成 \(\mathrm{M}=\{Q,\Sigma,\delta,q_1,F\}\),其中 \(Q=\{q_1,q_2,q_3\}\),\(\Sigma=\{0,1\}\),起始状态为 \(q_1\),\(F=\{q_2\}\),\(\delta\) 描述为
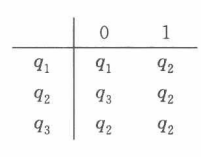
\(\mathrm{M}\) 的语言 \(L\) 为
非确定性
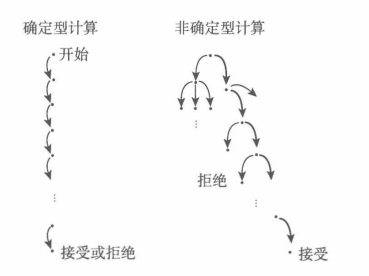
非确定型 计算是 确定型 计算的推广,在确定型计算中,机器每一步的计算都是按照唯一的转移法则,根据下一个输入的符号确定下一个状态。但是在非确定型计算中,转移法则不是唯一的。
有穷自动机也存在这两个种类,分别为 确定型有穷自动机 \(\text{(DFA)}\) 和 非确定型有穷自动机 \(\text{(NFA)}\)。上面的例子是一个 \(\text{DFA}\)。对于在 \(\text{NFA}\) 上的某个状态上的某个输入字符,我们会指定若干个转移的方式,甚至不指定对应的转移,机器会并行地执行所有分支,即使某一个分支由于不存在对应的转移而直接结束,整个计算也不会结束。最后,若存在一个分支在最后到达了一个接受状态,那么输出接受,否则输出拒绝。
另外,在 \(\text{NFA}\) 中我们新增一种转移为 \(\varepsilon\),当我们转移到一个状态 \(q\) 且 \(q\) 有射出的 \(\varepsilon\) 转移,无需输入任何字符,机器自动新建一个线程转移到 \(\varepsilon\) 指向的状态。
接下来我们形式化地定义非确定型有穷自动机和在它上面的计算:
「非确定型有穷自动机」 是一个五元组 \(\mathrm{N}=\{Q,\Sigma_{\varepsilon},\delta,q_0,F\}\),其中
$1.\ $ \(Q\) 是有穷的状态集。
$2.\ $ \(\Sigma_{\varepsilon}=\Sigma\cup\{\varepsilon\}\) 是有穷的字母表。
$3.\ $ \(\delta:Q\times\Sigma_{\varepsilon}\rightarrow \mathcal{P}(Q)\) 是转移函数,其中 \(\mathcal{P}(Q)\) 表示 \(Q\) 的所有子集组成的集合。
$4.\ $ \(q_0\in Q\) 是起始状态。
$5.\ $ \(F\subseteq\) 是接受状态集。
设 \(w=w_1w_2\cdots w_n\) 是一个字符串,如果存在 \(Q\) 中的状态序列 \(r_1,r_2,\cdots,r_n\) 满足下述条件:
$1.\ $ \(r_0=q_0\)
$2.\ $ \(r_{i+1}\in\delta(r_i,w_{i+1})\) 对于 \(i=0,1,\cdots,n-1\)
$3.\ $ \(r_n\in F\)
则称 \(\mathrm{N}\) 接受 \(w\)。
\(\text{NFA}\) 与 \(\text{DFA}\) 的计算能力
在自动机上进行的计算即为识别语言,那么它们识别语言的能力就代表了它们的计算能力。后面我们会讨论有穷自动机识别的语言类,即正则语言,为此这里我们先研究一下 \(\text{DFA}\) 和 \(\text{NFA}\) 的计算能力有何区别。
直觉上来说,\(\text{NFA}\) 的计算能力似乎比 \(\text{DFA}\) 更强,因为它可以并行计算,用更简单的状态来识别同样的语言。对于两台自动机识别同样的语言,那么称它们是 等价 的,令人惊奇地是,\(\text{NFA}\) 和 \(\text{DFA}\) 是等价的,即 每一台非确定型有穷自动机都等价于某一台确定型有穷自动机。
证明 对于一台有 \(n\) 个状态的 \(\text{NFA}\),我们考虑用 \(\text{DFA}\) 模拟它的所有并行线程,即维护在原机器中的当前状态子集。为此,新 \(\text{DFA}\) 的每个状态都应该对应原机器的一个状态子集,共有 \(2^n\) 个状态,若最后状态中包含一个在原机器中的结束状态,那么输出接受,否则输出拒绝。
形式化地,设 \(\mathrm{N}=(Q,\Sigma_{\varepsilon},\delta,q_0,F)\) 为一台识别语言 \(A\) 的 \(\text{NFA}\),下面考虑构造一台识别语言 \(A\) 的 \(\text{DFA}\) \(\mathrm{M}=(Q',\Sigma,\delta',q_0',F')\)。
设 \(E(R)\) 为所有从任意一个 \(q\in R\) 开始经过 \(0\) 个或多个 \(\varepsilon\) 转移可以到达的状态集合。
$1.\ $ \(Q'=\mathcal{P}(Q)\)。
$2.\ $ \(\delta'(R,a)=\bigcup_{r\in R}E(\delta(r,a)),R\in Q'\)。
$3.\ $ \(q_0'=E(\{q_0\})\)。
$4.\ $ \(F'=\{R\in Q'|\exist r\in R,r\in F\}\)。
经过这样构造,我们在 \(\mathrm{N}\) 和 \(\mathrm{M}\) 上同时输入一个字符串,对于每个输入字符,\(\mathrm{M}\) 所处的状态恰好是 \(\mathrm{N}\) 此时可能处于的状态集合,且若 \(\mathrm{N}\) 中此时的状态集合中有接受状态,那么对应的 \(\mathrm{M}\) 的状态也是一个接受状态。于是 \(\mathrm{N}\) 识别的语言与 \(\mathrm{M}\) 相同,两者等价。
正则语言
接下来我们将讨论有穷自动机的计算能力和它的局限性。如我们之前所言,有穷自动机识别一类特别的语言。
如果一个语言可以被一台有穷自动机识别,则称它是 「正则语言」 \(\text{(regular language)}\)。
语言的 「正则运算」 \(\text{(regular operation)}\) 是下面三种运算:
设 \(A,B\) 是两个语言,那么有
- 并:\(A\cup B=\{x|x\in A\text{ or } x\in B\}\)
- 连接:\(A\circ B=\{xy|x\in A\text{ and } y\in B\}\)
- 星号:\(A^{*}=\{x_1x_2\cdots x_k|k\geq 0\text{ and } x_i\in A\}\)
正则语言在正则运算下封闭。
证明大概是利用识别原语言的自动机构造出识别新语言的自动机,这里我们大致描述一下证明思路而不形式化说明了,正确性比较显然。
设 \(N_1,N_2\) 分别是识别 \(A\) 和 \(B\) 的非确定型有穷自动机。
并:并行处理两个自动机。
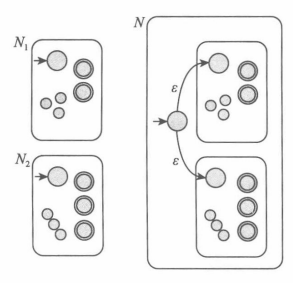
新建一个起始状态并射出两个 \(\varepsilon\) 转移分别指向 \(N_1\),\(N_2\) 的起始状态。
连接:先运行 \(N_1\),但凡找到了一段 \(A\) 中的串就新建一个线程将后面一段输入给 \(N_2\) 识别。
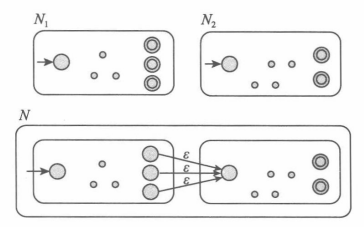
起始状态设为 \(N_1\) 的起始状态,对于每个 \(N_1\) 中的结束状态都射出一个 \(\varepsilon\) 转移指向 \(N_2\) 的起始状态,置结束状态集合为 \(N_2\) 的结束状态集合。
星号:先运行 \(N_1\),但凡找到了一段 \(A\) 中的串就新建一个线程将后面一段返回到 \(N_1\) 的起始状态继续识别。
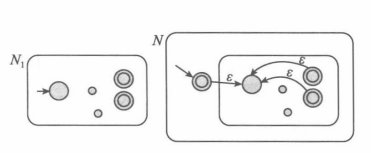
新建一个状态作为起始状态,并且它也是一个接受状态,这是为了接受星号中的空串。从它射出一个 \(\varepsilon\) 转移指向 \(N_1\) 的起始状态,从所有 \(N_1\) 的接受状态上射出一个 \(\varepsilon\) 转移指向起始状态。
接下来介绍语言的 正则表达式,它以另外一个形式等价地定义了正则语言。
称 \(R\) 是一个 「正则表达式」,如果 \(R\) 是
$1.\ $ \(a\),这里 \(a\) 是字母表 \(\Sigma\) 上的一个符号。
$2.\ $ \(\varepsilon\),这里 \(\varepsilon\) 是空串。
$3.\ $ \(\emptyset\),这里 \(\emptyset\) 是空语言。
$4.\ $ \((R_1\cup R_2)\),这里 \(R_1\) 和 \(R_2\) 是正则表达式。
$5.\ $ \((R_1\circ R_2)\),这里 \(R_1\) 和 \(R_2\) 是正则表达式。
$6.\ $ \((R_1^{*})\),这里 \(R_1\) 是正则表达式。
每个正则表达式都如逐个按照规则运算描述一个语言。例如设 \(\Sigma=\{0,1\}\), \((\Sigma\Sigma)^{*}\) 为长度为偶数的字符串组成的语言, \(1^{*}(01^{+})^{*}\) 表示每一个 \(0\) 后都至少跟有一个 \(1\) 的字符串组成的语言。其中 \(R^{+}\) 表示 \(RR^{*}\),即至少有 \(1\) 个 \(R\) 连接构成的语言。
正则表达式与有穷状态机具有等价性:一个语言是正则语言,当且仅当可以用正则表达式描述它。
证明 先证充分性。
设正则表达式 \(R\) 描述了一个语言 \(A\),考虑构造一个识别 \(A\) 的 \(\text{NFA}\) \(\mathrm{N}\)。对于正则表达式的 \(6\) 条定义,前 \(3\) 条是容易的,后 \(3\) 条可以直接用证明正则语言在并,连接,星号运算下封闭中的构造。
再证必要性。
设语言 \(A\) 是正则语言,需要证明有一个正则表达式描述它。由于 \(A\) 是正则语言,故存在一台 \(\text{DFA}\) \(\mathrm{M}\) 接受它,接下来我们将说明如何将 \(\mathrm{M}\) 转化为一个正则表达式。
首先将 \(\mathrm{M}\) 转化为一个等价的特殊形式的 广义非确定性有穷自动机 \(\text{(GNFA)}\) \(\mathrm{G}\),这里 \(\text{GNFA}\) 与 \(\text{NFA}\) 的区别是 \(\text{GNFA}\) 转移上的标号可以是一个正则表达式而非必须是符号,其余定义如 \(\text{NFA}\) 一样。特殊形式是指 \(\mathrm{G}\) 的起始状态到其余每一个状态都射出一个转移,接收状态仅有一个,且从其余每一个状态都射入一个转移,除了这两个状态,每一个状态到自身和其余状态都射出一个转移。
为此,首先新建一个起始状态,射出一个 \(\varepsilon\) 转移到原起始状态,新建一个接受状态,从所有原接受状态射入一个 \(\varepsilon\) 转移。如果一个转移上有多个标号,将其替换为一个标号为原先标号的并集的转移。最后在缺少转移的地方加入标号为 \(\emptyset\) 的转移。
接下来我们将说明一种方法来构造比 \(\mathrm{G}\) 的状态数少 \(1\) 的等价 \(\text{GNFA}\) \(\mathrm{G}'\),运用这种方法直到 \(\mathrm{G}\) 的状态数为 \(2\),此时 \(\mathrm{G}\) 仅有一个起始状态,一个接受状态和一个转移,这个转移上的正则表达式即为与 \(\mathrm{M}\) 等价的正则表达式。
首先任意选择一个非起始或接受的状态 \(q_{r}\),将它和关联它的转移从 \(\mathrm{G}\) 中删除,对于剩余的所有状态对 \((q_i,q_j)\),由于 \(\mathrm{G}\) 的特殊形式,在原自动机中 \(q_i\) 到 \(q_r\),\(q_r\) 到 \(q_r\),\(q_r\) 到 \(q_j\) 和 \(q_i\) 到 \(q_j\) 间都存在转移,设这四个转移上的正则表达式分别为 \(R_1,R_2,R_3,R_4\),那么 \(\mathrm{G'}\) 中从 \(q_i\) 到 \(q_j\) 的转移上的标号为
现在证明 \(\mathrm{G'}\) 和 \(\mathrm{G}\) 是等价的,假设 \(\mathrm{G}\) 接受字符串 \(w\),那么存在一个接受 \(w\) 的状态序列 \(q_{\text{start}},q_1,q_2,\cdots,q_{\text{accept}}\),设这个序列中存在若干段形如 \(q_i,q_r,\cdots,q_r,q_j\) 的状态序列,由于新添加的转移描述了从 \(q_i\) 到 \(q_r\) 到 \(q_j\) 的所有字符串,所以将其中的 \(q_r\) 删除后的状态序列是 \(\mathrm{G'}\) 中一个接受 \(w\) 的状态序列。另外一个方向也能这样直接推得。
故这个方法是正确有效的,我们将这个过程进行直到仅剩两个状态,此时可以得到与 \(\mathrm{M}\) 等价的正则语言 \(R\)。
再来回顾我们在前面定义的正则文法,一个正则文法 \(G=(V,\Sigma,R,S)\) 中的产生式的形式为下面三种
其中 \(a\) 是终结符,\(A,B\) 是变元。奇妙的是它也像前面两个方式一样定义了正则语言:一个语言是正则语言,当且仅当它可以由一个正则文法生成。
证明 先证充分性。
设 \(G=(V,\Sigma,R,S)\) 是一个正则文法,考虑构造识别 \(L(G)\) 的 \(\text{NFA}\) \(\mathrm{N}\)。令 \(Q=\{q_0,q_{\text{accept}}\}\cup V\);对于每个 \(A\rightarrow a\) 的产生式,建立一个从 \(A\) 到 \(q_{\text{accept}}\) 的标号为 \(a\) 的转移,对于每个 \(A\rightarrow aB\) 的产生式,建立一个从 \(A\) 到 \(B\) 的标号为 \(a\) 的转移;如果 \(G\) 中没有 \(S\rightarrow\varepsilon\) 的产生式那么 \(F=\{q_{\text{accept}}\}\),否则 \(F=\{q_{\text{accept}},q_0\}\)。
下面我们说明 \(\mathrm{N}\) 能识别 \(L(G)\)。如果 \(w=a_1a_2\cdots a_n\in L(G)\),观察产生式的形式,我们发现每次生成后的串中的变元只可能在最右边且数量为 \(1\) 或 \(0\),假设没有使用 \(S\rightarrow\varepsilon\) 的产生式,那么派生过程就为 \(S\Rightarrow a_1A_1\Rightarrow a_1a_2A_2\Rightarrow\cdots\Rightarrow a_1a_2a_3\cdots a_{n-1}A_{n-1}\Rightarrow a_1a_2\cdots a_{n-1}a_n\),采用的产生式序列为 \(S\rightarrow a_1A_1,A_1\rightarrow a_2A_2,\cdots, A_{n-1}\rightarrow a_n\),根据 \(\mathrm{N}\) 的构造,上面的产生式对应转移 \(q_0\stackrel{a_1}\rightarrow A_1,A_1\stackrel{a_2}{\rightarrow} A_2,\cdots,A_{n-1}\stackrel{a_n}{\rightarrow}q_{\text{accept}}\),故输入 \(w=a_1a_2\cdots a_n\) 后 \(\mathrm{N}\) 到达一个接受状态。如果采用了 \(S\rightarrow\varepsilon\) 的产生式,那么派生过程为 \(S\Rightarrow a_1A_1\Rightarrow a_1a_2A_2\Rightarrow\cdots\Rightarrow a_1a_2\cdots a_{n-1}a_{n}S\Rightarrow a_1a_2\cdots a_{n-1}a_n\),相当于上面的最后转移到了 \(q_0\),而由于此时 \(q_0\in F\),\(\mathrm{N}\) 仍然接受 \(F\)。反向亦然。
再证必要性。
设 \(L\) 是一个正则语言,\(\mathrm{M}=(Q,\Sigma,\delta,q_0,F)\) 是识别它的 \(\text{DFA}\),考虑根据它构造生成 \(L\) 的文法正则文法 \(G=(V,\Sigma',R,S)\)。令 \(V=Q\),\(\Sigma'=\Sigma\),\(S=q_0\),对于每个转移 \(q\stackrel{a}{\rightarrow} f\),其中 \(f\in F\),添加产生式 \(q_0\rightarrow a\),对于每个转移 \(p\stackrel{a}{\rightarrow} q\),添加产生式 \(p\rightarrow aq\),如果 \(q_0\in F\),那么添加产生式 \(S\rightarrow\varepsilon\)。
正确性也能类比上面的那个,挺显然的 \(\text{qwq}\),不想写了。
于是我们得到正则语言类的三个等价定义方式:有穷状态机,正则表达式,正则文法。
是正则语言吗?
有穷状态机的计算能力也是有限的,现在我们来讨论一些有穷状态机无力识别的语言和判断它们的方法。
没有存储空间是有穷状态机的一大硬伤,它将把所有当前需要用到的信息都放在一个状态里。比如语言 \(\{0^{n}1^{n}|n\geq 0\}\),如果要识别它,那么机器需要记住当前输入了多少个 \(0\),而 \(0\) 的个数是没有限制的,这意味着我们要准备无限个状态来记住当前输入了多少个 \(0\),但是它是 “有穷” 状态机。
下面说明一个判定正则语言的定理:「泵引理」 \(\text{(pumping lemma)}\)。它给出了一个语言是正则语言的必要条件。
若 \(A\) 是一个正则语言,则存在一个称之为泵长度的数 \(p\),使得如果 \(s\) 是 \(A\) 中任一长度不小于 \(p\) 的字符串,那么 \(s\) 可以被分成三段 \(s=xyz\) 满足:
$1.\ $ 对于每一个 \(i\geq 0\),\(xy^{i}z\in A\)。
$2.\ $ \(|y|\geq 0\)。
$3.\ $ \(|xy|\leq p\)。
通俗地理解这个定理,大致就是对于一个正则语言中所有长度不小于泵长度的的字符串,都可以从其中 “抽取” 一段非空子串,把它重复任意次后得到的字符串仍然在这个语言中。对于泵长度,我们知道它是存在的,但是不知道具体值是多少,也可能这个语言中根本没有长度不小于泵长度的字符串,这样的情况也是会出现的。
证明 设 \(A\) 是一个正则语言,那么存在 \(\mathrm{M}=(Q,\Sigma,\delta,q_0,F)\) 为一台识别 \(A\) 的 \(\text{DFA}\),令泵长度 \(p\) 为 \(A\) 的状态数。
设 \(s=s_1s_2\cdots s_n\in A\),且 \(n\geq p\),设 \(r_1r_2\cdots r_{n+1}\) 为 \(A\) 接受 \(s\) 时的状态序列,根据抽屉原理,在这个序列的前 \(p+1\) 个状态中必存在两个状态是重复的,设前一个为 \(r_i\),后一个为 \(r_j\),令 \(x=s_1s_2\cdots s_{i-1}\),\(y=s_is_{i+1}\cdots s_{j-1}\),\(z=s_js_{j+1}\cdots s_n\)。输入 \(x\) 后,\(\mathrm{M}\) 由 \(r_1\) 转移到 \(r_i\);输入 \(y\) 后,\(\mathrm{M}\) 由 \(r_i\) 转移到 \(r_j=r_i\),故接着可以输入任意次 \(y\),仍然转移到 \(r_j\);输入 \(z\) 后,\(\mathrm{M}\) 由 \(r_j=r_i\) 转移到 \(r_{n+1}\),而 \(r_{n+1}\) 是一个接受状态,故满足条件 \(1\)。由于 \(i\neq j\),故 \(|y|>0\),满足条件 \(2\)。又由于 \(j\leq p+1\),故 \(|xy=s_1s_2\cdots s_{j-1}|\leq p\),满足条件 \(3\)。
下面我们考虑用泵引理来证明开头的语言 \(B=\{0^{n}1^{n}|n\geq 0\}\) 不是正则语言。采用反证法,假设 \(B\) 是正则语言,令 \(p\) 为泵引理给出的泵长度,\(s=0^p1^p\in B\),它应该满足泵引理的三个条件。考虑从其中抽取一段 \(y\) 并重复它。由于条件 \(3\),\(y\) 在前半段,即 \(y\) 中只有 \(0\),这样的话重复一次后 \(s\) 中的 \(0\) 数量比 \(1\) 多,不是 \(B\) 的成员,矛盾。故假设不成立,\(B\) 不是正则语言。
再举一个应用泵引理的有趣例子:\(C=\{1^{n^2}|n\geq 0\}\)。继续采用反证法:设 \(C\) 是正则语言,\(p\) 为泵引理给出的泵长度。取 \(s=1^{p^2}\in C\),它一定可以被抽取,寻找矛盾。考虑 \(s=xyz\) 和 \(s'=xy^2z\),我们有 \(|xy|\leq p\),故 \(|y|\leq p\),又由于 \(|s|=p^2\),有 \(|s'|=|s|+|y|\leq p^2+p< p^2+2p+1=(p+1)^2\),并且 \(|y|>0\) 说明 \(|s'|=|s|+|y|>|s|=p^2\),这就得到 \(p^2<|s'|<(p+1)^2\),它的长度不是一个完全平方数,即 \(s'=xy^2z\notin C\),假设不成立, \(C\) 不是正则语言。
后记
这是可爱的企鹅看计算理论导引 \(\text{(Introduction to the Theory of Computation,Michael Spiser)}\) 以及离散数学及其应用 \(\text{(Discrete Mathmatics and Its Applications,Keeneth H. Rosen)}\) 的笔记,其中大部分(或者全部)的例子,配图和证明都来自于本书中,当然后续有时间会更新后面习题的记录之类,如果期中考试能够考的比较好来给我创造更多空余时间...
习题
来自计算理论导引第三版第一章习题的问题部分。皆为本人口胡www
\([1.31]\) 找到识别 \(A\) 和 \(B\) 的 \(\text{DFA}\) \(\mathrm{M}_1\) 和 \(\mathrm{M}_2\)。在它们的基础上构造识别 \(P\) 的自动机 \(\mathrm{M}\)。
大致思路是将输入串在 \(\mathrm{M}_1\) 和 \(\mathrm{M}_2\) 上并行计算,并且轮流将输入的字符给两边进行计算,比如输入 \(abcde\) 时,在 \(\mathrm{M}_1\) 中输入 \(ace\),在 \(\mathrm{M}_2\) 中输入 \(bd\),若两边都接受则接受,否则拒绝。
对于一个状态 \(q\) 将它拆成两个状态 \(q_{\text{in}}\) 和 \(q_{\text{out}}\) 以做到输入一个符号后 “等待” 一个字符再进行输入的目的。原本射入 \(q\) 的转移现在射入到 \(q_{\text{in}}\),原本从 \(q\) 射出的转移现在从 \(q_{\text{out}}\) 射出,然后设置一个由 \(q_{\text{in}}\) 到 \(q_{\text{out}}\),标号为所有符号的转移。若 \(q\) 是接受状态则 \(q_{\text{in}}\) 和 \(q_{\text{out}}\) 都是接受状态。最后将 \(\mathrm{M}_1\) 的起始状态拆成的两个 \(q_{\text{in}}\) 和 \(q_{\text{out}}\) 中的 \(q_{\text{in}}\) 删掉,改起始状态为 \(q_{\text{out}}\)。
对 \(\mathrm{M}_1,\mathrm{M}_2\) 做完上面的修改后,开始构造 \(\mathrm{M}\)。令 \(Q'=Q_1\times Q_2\),\(q_0\) 是 \(\mathrm{M}_1\) 的起始状态,\(F=F_1\times F_2\),\(\delta\) 为
\([1.32]\) 在上一题的基础上,我们在每个状态上 “等待” 的符号个数不确定了。摒弃上一题拆状态的构造,直接令每个状态上往自己转移一个 \(\varepsilon\) 然后再组合成 \(\mathrm{M}\)。
\([1.33]\) 用非确定性枚举该从哪里断开。把识别 \(A\) 的 \(\text{DFA}\) \(\mathrm{M}\) 复制一份为 \(\mathrm{M}'\),把 \(\mathrm{M}\) 中所有的结束状态去掉后作为上层,\(\mathrm{M'}\) 作为下层。对于 \(\mathrm{M}\) 中的每个转移 \(p\stackrel{a}{\rightarrow}q\) 都新建一个从上层到下层的 \(\varepsilon\) 转移 \(p\stackrel{\epsilon}{\rightarrow}q'\)。最后设起始状态为 \(\mathrm{M}\) 的起始状态。
\([1.34]\) 找到识别 \(B\) 和 \(C\) 的 \(\text{DFA}\) \(\mathrm{M}_1\) 和 \(\mathrm{M}_2\)。然后把 \(\mathrm{M}_2\) 中的所有 \(0\) 转移改成 \(\varepsilon\) 转移,这样在 \(\mathrm{M}_2\) 中输入一个串 \(w\) 后的状态集合为所有和 \(w\) 含有同样个数的 \(1\) 的串输入原自动机后到达的状态集合。
并行地计算 \(\mathrm{M}_1\) 和修改后的 \(\mathrm{M}_2\),当且仅当 \(\mathrm{M}_1\) 和 \(\mathrm{M}_2\) 都接受的时候输出接受。
\([1.35]\)
\([1.36]\) 找到识别 \(A\) 的 \(\text{DFA}\) \(\mathrm{M}\),然后反向它的所有转移,设起始状态为接受状态,接受状态取消,然后用一个新起始状态对所有原接受状态射出 \(\varepsilon\) 转移。
\([1.37]\) 首先因为二进制串从低位往高位输入是比较自然的,转化为证明 \(B^{\mathcal{R}}\) 是正则的。
我们维护两个值,一个是前两行的和的当前位和进位,一个是第三行的当前位,若前两行没有产生进位且前两位的和的当前位和第三行的当前位不同,那么一定是不同的,直接拒绝。到最后如果对应位全部相同且没有多的进位,那么接受,否则拒绝。
\([1.38]\) 类似上一题,只要认为第一行的 \(1\) 等价为 \(3\) 个 \(1\)。
\([1.39]\) 类似上一题,只要认为当前位第一行为 \(1\) 而第二行为 \(0\) 那么接受。
\([1.40]\) 如果 \(E\) 是正则的,令 \(p\) 是泵长度,\(s\in E\) 为
由于 \(|xy|\leq p\) 我们只能抽取前半段,而上一行是下一行的翻转,它们的 \(01\) 数量首先要相同,但是前半段的上一行只有 \(0\),下一行只有 \(1\),无论如何抽取都会使得 \(01\) 数量不等,从而抽取后的 \(s'\notin E\),给出矛盾。
\([1.41]\) 做一个长度为 \(n\),转移标号为 \(a\),起始状态是结束状态的圈!
\([1.42]\) 只需证 \(B^{\mathcal{R}}\) 是正则的。
根据欧拉定理,\(2^{k}\bmod n\) 是以 \(\varphi(n)\) 来循环的。我们设状态为二元组 \((p,q)\),其中 \(p\) 表示当前输入的值 \(\bmod n\) 的结果,\(q\) 表示这个输入在循环节的第 \(q\) 位,那么按照在循环的某一位对应的 \(2^k\bmod n\) 值能在它们之间建立转移。结束状态是所有的 \((0,q)\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号