BUAA-OO-2022-Unit1 博客总结

BUAA-OO-2022-Unit1 博客总结

本单元的任务为表达式化简，经过3次作业迭代后支持常数、幂函数、三角函数、求和函数、自定义函数、括号嵌套以及函数嵌套。

架构分析

Method CogC ev(G) iv(G) v(G)
Lexer.Lexer(String) 0 1 1 1
Lexer.Lexer(String, HashMap<String, HashMap<Character, Integer>>) 0 1 1 1
Lexer.getCurToken() 0 1 1 1
Lexer.getDefinedFunc() 18 5 13 13
Lexer.getDefinedFuncs() 0 1 1 1
Lexer.getEndPos() 6 1 4 6
Lexer.getNextToken() 0 1 1 1
Lexer.getNum() 4 2 3 3
Lexer.getPos() 0 1 1 1
Lexer.getPowerFunc() 7 3 4 4
Lexer.getSumFunc() 4 2 3 3
Lexer.getTrigonoFunc() 16 2 8 8
Lexer.getTrigonoFuncFactor(String) 15 7 8 11
Lexer.next() 1 1 2 2
Lexer.toString() 0 1 1 1
MainClass.main(String[]) 1 1 2 2
Parser.Parser(Lexer) 0 1 1 1
Parser.Parser(Lexer, HashMap<String, HashMap<Character, Integer>>) 0 1 1 1
Parser.getTermSign() 4 2 3 3
Parser.parseExpression() 2 1 3 3
Parser.parseFactor() 21 7 8 11
Parser.parseTerm() 2 1 3 3
Pretreater.Pretreater(String) 0 1 1 1
Pretreater.Pretreater(String, HashSet) 0 1 1 1
Pretreater.deleteBlank() 0 1 1 1
Pretreater.deleteRedundantSign() 0 1 1 1
Pretreater.getDefinedFuncs() 10 1 5 5
Pretreater.pretreat() 0 1 1 1
Pretreater.toString() 0 1 1 1
Printer.Printer(Expr) 0 1 1 1
Printer.addFactorString(StringBuilder, Factor) 8 1 7 7
Printer.addNumString(StringBuilder, Num) 0 1 1 1
Printer.addPostiveTermString(StringBuilder, HashMap<HashSet, BigInteger>) 3 3 3 3
Printer.addPowerFuncString(StringBuilder, PowerFunc) 7 1 4 4
Printer.addTermCoefficient(StringBuilder, HashSet, BigInteger) 30 4 12 13
Printer.addTermString(StringBuilder, HashSet, BigInteger) 13 1 8 9
Printer.addTrigonoFuncString(StringBuilder, TrigonoFunc) 5 1 5 6
Printer.cloneMap(HashMap<HashSet, BigInteger>) 1 1 2 2
Printer.cloneSet(HashSet) 1 1 2 2
Printer.getEndPos(String) 6 1 4 6
Printer.getExpr() 0 1 1 1
Printer.getExprString() 5 2 4 4
Printer.getSimplifyExprString(String) 0 1 1 1
Simplifier.Simplifier(Expr) 0 1 1 1
Simplifier.addFactor(HashSet, Factor) 8 1 5 5
Simplifier.cloneSet(HashSet) 1 1 2 2
Simplifier.compareOtherFactor(HashSet, HashSet, Factor) 29 5 10 14
Simplifier.compareSet(HashSet, HashSet) 14 4 4 6
Simplifier.deleteRedundantTrigonoFunc(HashMap<HashSet, BigInteger>) 7 1 5 5
Simplifier.getSimplifiedExpr() 0 1 1 1
Simplifier.getTrigonoFuncIndex(HashSet, Factor, String) 4 3 5 5
Simplifier.mergeTrigonoFunc(HashMap<HashSet, BigInteger>, HashSet, HashSet, Factor, BigInteger, BigInteger) 26 1 12 12
Simplifier.symplifyIndexZeroTrigonoFunc(HashMap<HashSet, BigInteger>) 14 1 8 8
Simplifier.symplifyTerms(HashMap<HashSet, BigInteger>) 0 1 1 1
Simplifier.symplifyTrigonoFunc(HashMap<HashSet, BigInteger>) 39 10 10 13
Simplifier.symplifyTrigonoFuncNumFactor(HashMap<HashSet, BigInteger>) 13 1 8 8
Simplifier.symplifyTrigonoZero(HashMap<HashSet, BigInteger>) 15 3 9 11
expression.DefinedFunc.DefinedFunc(String, String, String, String, HashMap<String, HashMap<Character, Integer>>) 3 1 3 3
expression.DefinedFunc.clone() 0 1 1 1
expression.DefinedFunc.equals(Factor) 0 1 1 1
expression.DefinedFunc.getExpreesionString() 23 3 11 11
expression.Expr.Expr() 0 1 1 1
expression.Expr.Expr(HashMap<HashSet, BigInteger>) 0 1 1 1
expression.Expr.addTerm(Term) 31 5 10 10
expression.Expr.clone() 0 1 1 1
expression.Expr.cloneExpr(HashMap<HashSet, BigInteger>) 3 1 3 3
expression.Expr.compareHashSet(HashSet, HashSet) 14 6 4 6
expression.Expr.equals(Factor) 22 5 6 8
expression.Expr.getTerms() 0 1 1 1
expression.Expr.mergeHashSet(HashSet, HashSet) 44 1 14 14
expression.Expr.multiplyExpr(HashMap<HashSet, BigInteger>, HashMap<HashSet, BigInteger>) 13 5 6 6
expression.Expr.multiplySelf(BigInteger) 4 1 3 3
expression.Expr.toString() 5 2 4 4
expression.Num.Num(BigInteger) 0 1 1 1
expression.Num.clone() 0 1 1 1
expression.Num.equals(Factor) 1 1 2 2
expression.Num.getCoefficient() 0 1 1 1
expression.Num.toString() 0 1 1 1
expression.PowerFunc.PowerFunc(String, BigInteger) 0 1 1 1
expression.PowerFunc.clone() 0 1 1 1
expression.PowerFunc.equals(Factor) 1 1 3 3
expression.PowerFunc.getIndex() 0 1 1 1
expression.PowerFunc.getVariable() 0 1 1 1
expression.PowerFunc.toString() 0 1 1 1
expression.SumFunc.SumFunc(String, BigInteger, BigInteger, String) 0 1 1 1
expression.SumFunc.clone() 0 1 1 1
expression.SumFunc.equals(Factor) 0 1 1 1
expression.SumFunc.getExpreesionString() 13 2 9 9
expression.SumFunc.getFactorString() 0 1 1 1
expression.SumFunc.getLoopVariable() 0 1 1 1
expression.SumFunc.getLowerLimit() 0 1 1 1
expression.SumFunc.getUpperLimit() 0 1 1 1
expression.Term.Term(String) 0 1 1 1
expression.Term.addExpr(Expr) 20 6 7 7
expression.Term.addFactor(Factor) 4 1 5 5
expression.Term.addNum(Num) 2 1 2 2
expression.Term.addPowerFunc(PowerFunc) 12 1 5 5
expression.Term.addTrigonoFunc(TrigonoFunc) 22 1 9 9
expression.Term.compareHashSet(HashSet, HashSet) 14 6 4 6
expression.Term.getFactors() 0 1 1 1
expression.Term.getSign() 0 1 1 1
expression.Term.mergeHashSet(HashSet, HashSet) 44 1 14 14
expression.TrigonoFunc.TrigonoFunc(String, Factor, BigInteger) 0 1 1 1
expression.TrigonoFunc.clone() 0 1 1 1
expression.TrigonoFunc.equals(Factor) 1 1 4 4
expression.TrigonoFunc.getFactor() 0 1 1 1
expression.TrigonoFunc.getIndex() 0 1 1 1
expression.TrigonoFunc.getTrigonoType() 0 1 1 1
expression.TrigonoFunc.toString() 0 1 1 1
Class OCavg OCmax WMC
Lexer 3.27 10 49
MainClass 2 2 2
Parser 3.17 10 19
Pretreater 1.57 5 11
Printer 3.71 12 52
Simplifier 5.36 11 75
expression.DefinedFunc 3 7 12
expression.Expr 4.67 13 56
expression.Num 1 1 5
expression.PowerFunc 1 1 6
expression.SumFunc 1.62 6 13
expression.Term 4.9 13 49
expression.TrigonoFunc 1 1 7
Package v(G)avg v(G)tot
4.28 244
expression 3.17 165
Module v(G)avg v(G)tot
Unit-1 3.75 409
Project v(G)avg v(G)tot
project 3.75 409

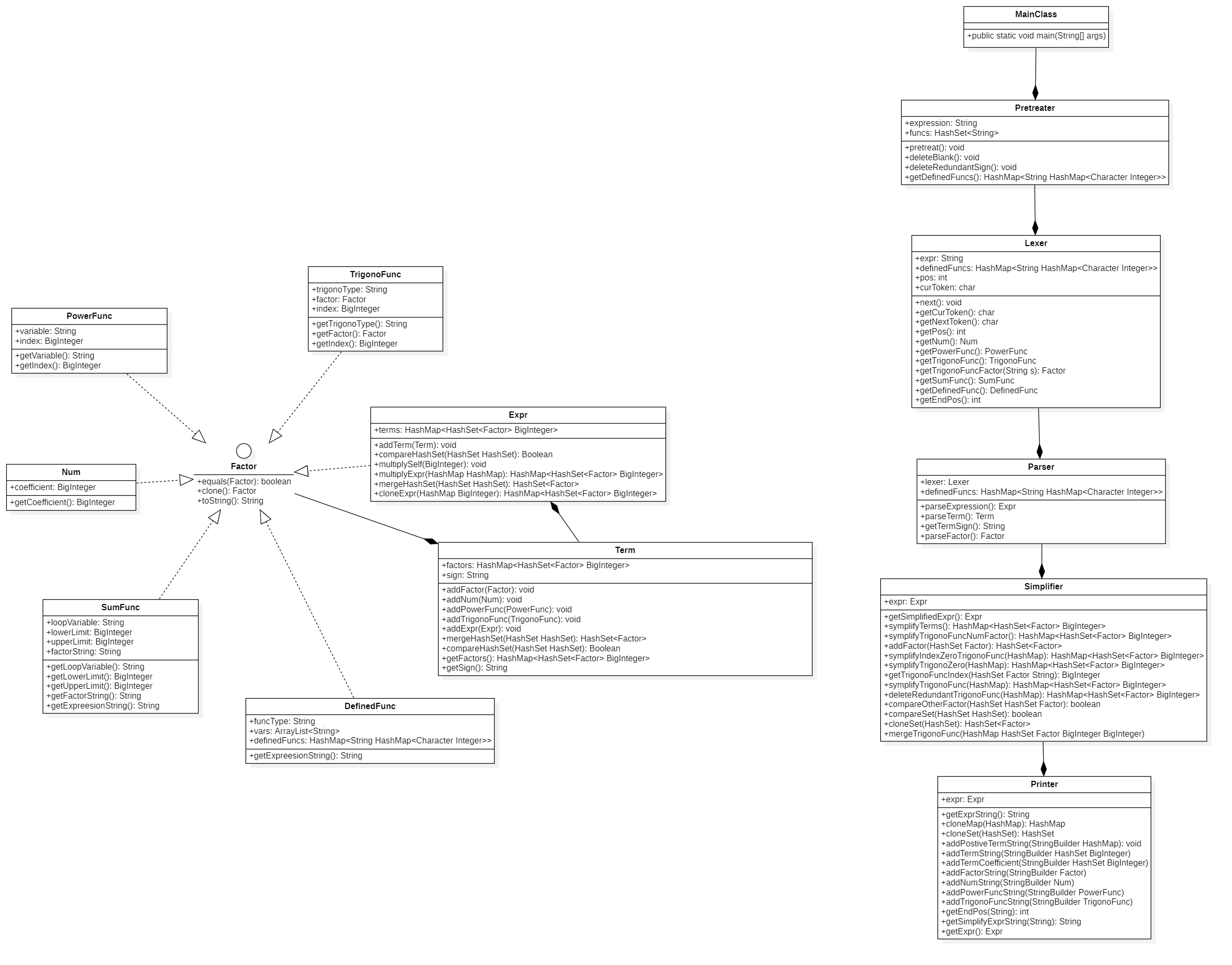
对于面向对象编程，笔者认为有两点至关重要，一是事先对项目架构的分析与设计，二是实现过程中对实现难度与拓展性的权衡。一个没有经过精心设计的架构，只能在早期应付相对简单的任务，当功能需求增加、功能复杂度提高时，迭代开发会使项目拓展性不断减低，导致后续功能的添加变得尤为困难；而不同模块间的耦合度很可能也会同时增加，进而破坏封装原则，使得项目调试难度陡增，更容易产生设计上的疏忽。

相反，在面对冗杂需求时，良好的设计模式与架构可以帮助编程人员将复杂问题缩小，逐个解决。并且设计模块之间互不影响，彼此仅通过接口联系，而不需要关注对方的实现细节。因此当一个模块出现问题时，我们仅需要修改其内部实现，而不需要考虑该模块的修改对其他模块的功能影响。

所谓实现难度与拓展性的权衡，就是我们在添加简单功能与bug修复时作出的选择，有时因为实现简单，我们会采取一种“打补丁”的方式对程序或项目进行开发或修复，但如果“补丁”越来越多，可能会导致项目拓展性的严重下降。因此在理想情况下，我们希望无论是功能添加还是$bug$修复，都能够优雅地进行，尽可能维持项目的拓展性。但现实情况是，有时针对简单问题的强行解耦略显突兀，可能带来开发难度的大幅提升，因此在这其中我们就需要作出权衡，后文会体现这一点。

输入

在本单元中，笔者对待解析表达式从输入到输出的各个环节进行了解耦，建立了Pretreater、Lexer、Parser、Simplifier、Printer等多个类，各司其责。而由于本单元输入较为简单，笔者选择直接在MainClass主类中进行，将输入得到的自定义函数字符串与待解析表达式字符串传递给Pretreater类，其中自定义函数字符串可以存储在一个ArrayList结构中。但通过课上老师的讲解，我认为针对输入还是应该建立一个Input类，这是因为目前我们仅是从标准控制台输入，而如果以后有从文件输入的需求，我们仅需要修改Input类而不需要对主类作出修改。

本模块仅需要以任意方式得到输入的字符串并传递给预处理模块，而不需要任何的处理、解析行为。

预处理

由于输入的字符串目前未经过解析模块，因此我们的预处理只能基于某些规则和规律进行，而无法在语义层面对字符串进行处理。

通过观察，笔者认为可以做如下预处理：

待解析表达式

处理顺序有时会对正确性造成影响，后文优化部分有相应例子。

  1. 去除表达式中所有的空白符与制表符

    this.expr = this.expr.replaceAll("[ \t]", "");

  2. 将连续的加号化简为一个加号

    this.expr = this.expr.replaceAll("\\+\\+", "+");

  3. 将连续的加号和减号化简为一个减号

    this.expr = this.expr.replaceAll("(\\+)?-(\\+)?", "-");

  4. 将连续的减号化简为一个加号

    this.expression = this.expression.replaceAll("--", "+");

  5. 将连续的星号和加号化简为一个星号

    this.expression = this.expression.replaceAll("\\*\\+", "*");

    这一步同时去除了乘法运算与乘方运算中的多余符号。

  6. 如果字符串第一个字符是加号，则替换为空字符

    this.expression = this.expression.replaceAll("^\\+", "");

自定义函数

该模块我们需要将输入类读入的函数定义字符串进行预处理，去除其中的空白符与制表符，然后将相应信息存储进某种利于后续函数调用的数据结构，笔者选择的数据结构是HashMap<String, HashMap<Character, Integer>>，外层HashMap通过经预处理的函数定义字符串进行索引，而内层HashMap记录函数定义时形参相应的位置。

比如f(y,x)=x+2*y处理后得到的<String,HashMap<Character,Integer>>为<f(y,x)=x+2*y, {<y,1>, <x,2>}>。

解析

该模块是我们要考虑的重中之重，也是我们真正开始解析表达式的第一个阶段，笔者通过分别建立Lexer类和Parser解决。在第一次作业中，由于限制括号嵌套，所以可能可以通过正则表达式实现解析，但笔者并没有尝试，这是由于先前提到的事先对项目架构的分析与设计，注意到如果后期需要解决嵌套括号，那么笔者在后续开发大概率需要进行重构，因此笔者在第一次作业便采取了一种名为递归下降的方法来对表达式进行解析，后期证明其大有裨益。

递归下降

以笔者粗浅的理解，递归下降的核心在于将多层次问题转化为单层问题，这降低了我们考虑问题的难度。并且递归下降提高了项目鲁棒性，这是由于我们只要正确地解决了单层问题，那么就可以确信我们能够正确地解决嵌套的多层次问题，即使这个表达式是由很多层复杂的因子与项组合起来的。

具体来说，站在表达式这个层次来观察表达式，它可能由多个+和-进行连接，我们将+和-连接的部分称为项；站在项这个层次来观察项，它可能由多个*进行连接，我们将*连接的部分称为因子；那么因子可能为什么？在第一次作业中，因子可能为带符号的整数、变元的幂以及由括号包裹的表达式；在第二次与第三次作业中，因子除了上述情况，还可能为三角函数、求和函数以及自定义函数，我们稍后依次进行分析。

因子接口

为后续在处理时可以统一管理因子类，笔者选择事先声明Factor接口，并要求所有实现Factor的类复写public boolean equals(Factor other)、public Factor clone()以及public String toString()方法。

因子类

老师曾在课上提到，类可以看作是我们作出的一种约定，而通过new得到的对象，则是真正存储在内存中的数据。对于外部来说，对象的属性并不重要，因此为了契合面向对象的封装思想，课程组要求我们在现阶段将所有类的属性定义为private类型，内部与外部通过public类型的方法进行通信，方法返回的是这个类型的状态，对象的状态可以反映对象的属性，但不能说对象的属性决定对象的状态。这就是说，我们在访问一个对象的时候，不需要考虑其内部真正的实现方式以及其对属性的存储的存储方式，我们只需要关注其返回给外部的状态。因此在介绍存储模块之前，笔者仅说明该类需要实现什么功能，返回什么状态，而暂时不关注类内部的实现方式。

Num

该类需要能够刻画一个带符号的整数，因此可以定义方法public BigInteger getCoefficient()。

PowerFunc

该类需要能够刻画一个变元的幂，因此可以定义方法public String getVariable()和public BigInteger getIndex()，在本单元任务中，变元被限定为x。

TrigonoFunc

该类需要能够刻画一个三角函数，三角函数内部为一个因子，因此可以定义方法public String getTrigonoType()、public Factor getFactor()、public BigInteger getIndex()，在本单元任务中，三角函数的种类被限定为sin和cos。

Expr

该类既可以视为因子类，也可以视为顶层类，是我们递归下降的难点。它需要能够等价刻画一个复杂的表达式，并利于索引，所以我们需要设计某种数据结构，笔者选择的数据结构是HashMap<HashSet<Factor>,BigInteger>，原因将在 存储模块详细介绍，我们暂时先在该类定义方法public HashMap<HashSet<Factor>, BigInteger> getTerms()。

SumFunc

该类需要能够刻画一个求和函数，我们注意到SumFunc展开后可以得到Expr，然后复用解析Expr的方法解析展开后的SumFunc，因此我们可以定义方法public String getLoopVariable()、public BigInteger getLowerLimit()、public BigInteger getUpperLimit()、public String getFactorString()，在本单元任务中，循环变量被限定为i。而事实上，外部更需要的是展开后的SumFunc，所以我们还需要定义方法public String getExpreesionString()，或者直接复写public String toString()。

那么如何得到展开后的SumFunc呢，我们只需要通过一个循环，在每次循环中将求和因子中的循环变量附加括号后进行替换，然后对求和因子累加即可。

事后笔者认为，我们完全可以将i视为与x类同的变元，而最初设计的因子类和Expr数据结构并不需要作出调整，所以我们可以不采取用String类型存储求和因子这样略显刻意的方法，直接复写因子类的public String toString()方法即可。

DefinedFunc

该类需要能够刻画一个自定义函数，笔者希望继续采取类似处理SumFunc的思路，即只需要对外返回等价代入后的Expr字符串，再复用Expr的解析方法。而由于我们选择将代入的工作放入该类内部进行，所以每次生成对象时，需要将记录有函数定义的数据传入这个对象。我们在该类定义方法public String getExpreesionString()，其实现原理是根据自定义函数的种类选择对应的函数定义字符串，然后从第一个字符开始进行遍历，当遇到形参x、y或z时则替换为相应位置的实参，同时可以在实参两端附加一对括号。

项类

由于嵌套括号的存在，Term类需要具有与Expr类相同的数据结构，即使用HashMap<HashSet<Factor>,BigInteger>来表示内部的数据。另外，笔者为Term类定义了sign属性来表示对象的正负，方便Expr类合并Term对象。Term类最主要的方法是public void addFactor(Factor factor)，而为了将方法解耦，笔者选择仅在该类中判断Factor实例的种类，然后选择对应的add方法：

public void addFactor(Factor factor) {
        if (factor instanceof Num) {
            addNum((Num) factor);
        } else if (factor instanceof PowerFunc) {
            addPowerFunc((PowerFunc) factor);
        } else if (factor instanceof TrigonoFunc) {
            addTrigonoFunc((TrigonoFunc) factor);
        } else if (factor instanceof Expr) {
            addExpr((Expr) factor);
        }
    }

由于在笔者的实现中，内层HashSet<Factor>的元素仅可能为变量的幂以及三角函数，故笔者选择在第一次addFactor时默认事先在外层HashMap中放入一个HashSet，其中包含一个次数为0的变量，比如x**0，确保外层HashMap中元素个数不为0。不然，如果第一次add``Factor因子种类为Num，处理起来稍有麻烦。

  1. public void addNum(Num num)：外层HashMap中默认存在元素，故我们只需要更新每一个key对应的value。

  2. public void addPowerFunc(PowerFunc powerFunc)：内层HashSet默认包含变量的幂，我们只需要更其指数。

  3. public void addTrigonoFunc(TrigonoFunc trigonoFunc)：我们需要遍历每一个内层HashSet，如果发现存在相同种类的三角函数，则更新其指数，否则将trigonoFunc直接放入。

  4. public void addExpr(Expr expr)：我们同样需要遍历每一个内层HashSet，实现类多项式的相乘，对于第一次addFactor因子种类为Expr的情况特判即可。

由于笔者选择将SumFunc以及DefinedFunc展开为Expr后再进行解析，故我们只需要定义addExpr(Expr expr)方法即可处理这两种函数。

词法分析器实现

该类主要负责进行词法分析，直观上讲可以将其视为一个游标，不断移动来分析待解析表达式的每一个字符，因此需要实现public void next()、public char getCurToken()、public char getNextToken()以及public int getPos()等方法，利于对外描述目前游标所指向的位置以及该位置的字符。同时，该类需要从待解析表达式中获取实例化因子类信息，因此笔者在该类实现了public Num getNum()、public PowerFunc getPowerFunc()、public TrigonoFunc getTrigonoFunc()、public SumFunc getSumFunc()以及public DefinedFunc getDefinedFunc()等方法来处理不同种类的因子，方法的调用受Parser模块的控制。

由于三角函数内部包含一个因子，所以笔者同时在Lexer内部设计public Factor getTrigonoFuncFactor(String s)方法，在通过public TrigonoFunc getTrigonoFunc()获取字符串形式的因子后，可以通过调用该方法实例化对应种类的因子并返回。该方法的实现思路是递归调用Lexer模块的其他get方法，通过返回值是否为null来判断因子种类。

另外，笔者在第一次作业中主要通过正则表达式来获取相应信息，但是由于第二次作业SumFunc、DefinedFunc以及第三次作业TrigonoFunc内部因子限制的解除，正则表达式不再能够满足题目的需求，这是因为因子可能有多层括号嵌套，正则表达式的设计变得较为困难，容易有纰漏。笔者当时选择的方法是在第二次作业与第三次作业Lexer模块中设计public int getEndPos()方法来维护一个括号栈，解决了正则表达式提取错误的问题。但笔者反思时认为，我们应尽可能不使用正则表达式，而要尽量从语义角度获取对应信息，除非特征信息非常简单。

解析模块实现

该类在递归下降中发挥关键作用，但主要仅包含三个方法，分别是public Expr parseExpression()、public Term parseTerm()以及public Factor parseFactor()。

parseExpression()通过未包含于括号中的+与-将待解析表达式拆开，逐一对每个部分调用parseTerm()，并将解析结果返回。

public Expr parseExpression() {
        Expr expression = new Expr();
        expression.addTerm(parseTerm());
        while (lexer.getCurToken() == '+'
                || lexer.getCurToken() == '-') {
            expression.addTerm(parseTerm());
        }
        return expression;
    }

public Term parseTerm()通过未包含于括号中的*将待解析项拆开，逐一对每个部分调用parseFactor()，并将解析结果返回。而由于笔者在Term类定义了sign属性，故还需要设计public String getTermSign()方法，不过笔者后面认为该方法更适合出现在Lexer模块当中。

public Term parseTerm() {
        Term term = new Term(getTermSign());
        term.addFactor(parseFactor());
        while (lexer.getCurToken() == '*' && lexer.getNextToken() != '*') {
            lexer.next();
            term.addFactor(parseFactor());
        }
        return term;
    }

public String getTermSign() {
    if (lexer.getCurToken() == '-') {
        lexer.next();
        return "-";
    } else {
        if (lexer.getCurToken() == '+') {
            lexer.next();
        }
        return "+";
    }
}

public Factor parseFactor()类似于Lexer模块public Factor getTrigonoFuncFactor(String s)的实现思路，对于Expr以外的因子，仅需要通过调用Lexer模块的get方法并判断返回值是否为null来确定因子种类；而对于Expr我们只需要递归调用public Expr parseExpression()方法即可。关于表达式的幂次，笔者选择的方法是在Parser类获取指数，并调用Expr内部的public void multiplySelf(BigInteger index)方法。另一种实现思路是在Expr类定义index属性，这样或许可以在Lexer模块获取指数，在功能上更契合Lexer模块与Parser模块应有的作用。

存储

第一次作业

在第一次作业中，笔者采用了Expr→Term→Factor的解析思路，同时笔者注意到Expr与Term的通项均可以表示为一个多项式，因此我们可以通过一个HashMap<String, BigInteger>来对Expr和Term进行存储，其中多项式每一项a*x**b中的a和b可分别作为HashMap的value和key。

第二次作业

在第二次作业中，由于三角函数的引入，笔者在考虑Expr与Term的通项时遇到了困难。首先Expr和Term的通项由第一次作业的$\sum ax**b$拓展为$\sum axb_{i1}\Pi(\sin (f(x))b_{i2})\Pi(\cos (g(x))b_{i3})$，并可以进一步化归为$\sum\lambda\Pi G(f(x))\alpha$，其中：

$G(f(x))\to x;|;TrigonoFunc$

$TrigonoFunc\to\sin ⁡f(x);∣;cos⁡f(x)$

$f(x)\to PowerFunc;∣;Num$

$PowerFunc\to x**\alpha,;\alpha\in N^*$

$Num\to带符号的整数$（正数和零前无符号，负数前有一个负号）

Num→带符号的整数Num→带符号的整数（正数和零前无符号，负数前有一个符号"-"）

因此笔者希望设计一种便于检索合并的数据结构来对此通项进行存储。

我们提出的方式：[两层HashMap嵌套]

  • 外层HashMap：HashMap<(Inner HashMap), BigInteger>，其中BigInteger存储前置系数$\lambda$。
  • 内层HashMap ：HashMap<String, BigInteger>，其中String存储三角表达式或幂函数底数x的字符串形式，BigInteger存储三角表达式或x的幂次。

具体解析策略

为方便起见，我们定义一个HashMap可以表示为{$(a_1,b_1),(a_2,b_2),\cdots,(a_n,b_n)$}。本策略采用边解析边合并的方式进行存储：

  1. 解析Num时，我们需更新外层HashMap每一项元素对应的value。
  2. 解析PowerFunc时，我们需更新外层HashMap所有key对应的HashMap中key为x的元素的value。
  3. 解析TrigonoFunc时，我们需更新外层HashMap中所有kkey对应的HashMap，如果先前已存储过相同的TrigonoFunc，则只需要更新内层HashMap中key为该TrigonoFunc的元素对应的value；若先前未存储过，则可直接push元素。
  4. 解析求和函数、自定义函数或表达式时，将其对应的外层HashMap与此Term已有的外层HashMap合并。
  5. 解析第一个Factor时，默认在内层HashMap中put一个key为x的元素。

例：解析表达式sin(x)*x*2*-3*(1+x+2*sin (x*2)**3)

根据上述法则，逐步解析得到的外层HashMap如下：

第一步：{({("sin(x)",1),("x",0)},1)}

第二步：{({("sin(x)",1),("x",2),1)},1)}

第三步：{({("sin(x)",1),("x",2)},−3)}

第四步：{({("sin(x)",1),("x",2)},−3),({("sin(x)",1),("x",3)},−3),({("sin(x)",1),("x",3),("sin(x∗∗2)",3)},−6)}

6.后期对两个简单项进行合并时（每个简单项分别对应于一个内层HashMap），我们首先比较两个内层HashMap的size()是否相等；若相等，则对其中一个内层HashMap进行遍历，如果此时遍历的key同时出现在另一个内层HashMap中，且value相等，则继续比较，否则可以提前判断这两个简单项不可合并。若两个简单项可合并，则只需要将内层HashMap对应的外层HashMap的value相加。

这样做的好处：存储结构简明、对不同项只需要反复调用HashMap、输出较易。

第三次作业

由于三角函数内部因子限制的解除，内层HashMap继续使用String类型作为key不能满足嵌套的需求，故我们将String更换为Factor，并且此时笔者发现，因子的次数信息已包含Factor中，故笔者在第三次作业中使用了HashMap<HashSet<Factor>,BigInteger>作为存储的数据结构，解析与存储的策略仍然类似于第二次作业，实际改动并不大。

化简

切莫压点提交，并且要先保证正确性，再考虑性能上的优化。

该类主要负责完成Term层面的优化，具体内容将在优化策略中介绍。

输出

该类主要负责完成输出层面的优化，并返回解析后表达式的字符串，具体内容同样将在优化策略中介绍。

优化策略

Term优化

笔者作出的优化有：

  1. 将0次幂因子化简为1，事实上可以直接删除。
  2. 将幂次为奇、内部因子种类为Num且Num为负数的三角函数符号外提，判断是否可与其他项合并。
  3. 将sin(0)化简为0，将cos(0)化简为1。
  4. 对于$sin(f(x)){a_{1}}cos(f(x))G(x)+sin(f(x)){a_2}cos(f(x))G(x)$，若满足$|a_1-a_2|=2&&(a_1-a_2)(b_1-b_2)=-4$，则可进行平方和合并。

优化顺序将影响正确性，笔者在第三次作业中误选择先去除包含sin(0)的项，再化简0次幂因子，导致笔者将sin(0)**0输出为0。

输出优化

笔者作出的优化有：

  1. 对于1*G(x)输出G(x)，-1*G(x)输出-G(x)。
  2. 对于G(x)**1输出G(x)。
  3. 优先输出系数为正的项。
  4. 对于x**2输出x*x，在第三次作业中其可能导致负优化，比如sin(x**2)长度短于sin((x*x))。

易错点分析

HashMap与HashSet

  1. 对于HashMap，如果put元素的key先前已存在，则其会覆盖之前的数据。
  2. 对于HashMap，如果选择Object类型作为key，即使两个Object表达的状态相同，也不能通过一个Object索引另一个Object的value.
  3. 不要边遍历边修改HashMap和HashSet中的元素，这会导致错误遍历，甚至死循环。

深拷贝与浅拷贝

由于浅拷贝的存在，对象的不当赋值可能导致对象之间相互影响，因此笔者重写了所有因子类的public Factor clone()方法，来保证每次新对象的生成都是原有对象的深拷贝，确保对象之间不会相互影响。

正则匹配

对于嵌套括号，正则表达式的书写变得尤为困难，可以考虑：

  1. f(sin(x))+f(sin(x))

  2. f(sin(x),sin(x))+g(sin(x))

  3. f(sin(x),sin(x),sin(x))+g(sin(x))

故我们应尽可能从语义角度进行分析。

递归解析

多次预处理

由于笔者在处理SumFunc与DefinedFunc时选择对外返回待解析表达式字符串，故我们需要重新对字符串进行预处理，否则可能导致解析错误。

对象比较

笔者重写了所有因子类的public boolean equals(Factor other)方法，比较策略是：

  1. 实例类型是否相同，不相同返回false。
  2. 状态是否相同，不相同返回false。如果返回的状态类型为HashMap或HashSet，则需要逐一对内部元素的状态进行比较。
  3. 上述条件满足，返回true。

数据构造

在对自己程序进行验证或对其他人进行Hack时，首先需要仔细阅读指导书，确保自己对于指导书中的细节完全了解，避免被强测背刺，比如笔者在第二次作业中，疏忽了在函数定义中可以存在空格，导致解析错误。

对于黑盒测试，笔者认为可采取两种方式对程序进行验证和Hack，一是数据生成器随机轰炸，这种可以找出程序中基本的错误；二是对一些极端情况的数据构造，比如因子0次幂、指标溢出。

对于白盒测试，主要通过代码分析来找出程序中的漏洞，比如如果对方采取了正则表达式解析，则可以重点关注其表达式的书写是否有纰漏；如果对方进行复杂的优化，则可以重点关注优化部分的逻辑是否正确，是否可能发生TLE。

感受

通过本单元的学习，笔者对面向对象的思想有了初步的认识，并且有了一定代码风格的培养，最后，感谢课程组的辛勤奉献！

posted @ 2022-03-26 14:58  yufu06  阅读(98)  评论(1)    收藏  举报