后缀数组及其应用
这里简单介绍一下倍增算法\((O(nlogn))\)求后缀数组
定义
定义\(S\)是长度为\(n\)的字符串,后缀\(suf[i]\)指\(S[i\sim n]\);
将\(S\)的所有后缀按字典序排序:
- \(rk[i](rank[i])\)指\(suf[i]\)的排名;
- \(sa[i]\)指第\(i\)名的后缀是\(suf[sa[i]]\);
- \(height[i]\)指第\(i\)名和第\(i-1\)名后缀的最长公共前缀\((lcp)\);
算法原理
sa数组求法
求得\(sa\)数组也就求得了\(rk\);
首先我们可以很容易想到一个快排实现的算法,如果基于逐字符比较的算法时间是\(O(n^2logn)\);
我们也可以想到一个优化,用\(Hash+\)二分代替逐字符比较,这样时间是\(O(nlog^2n)\);
另外的想法:
可以把每个后缀看成由\(ASCII\)码构成的数列,用基数排序来实现,这样时间是\(O(n^2)\)的;
想办法优化:
因为待排序的字符串都是\(S\)上面的后缀,它们是有相同部分的;
这样我们可以引入这样的一个算法:
1.对于每个后缀的第一个字符进行一次排序,得到它们的排名作为每一个后缀的第一关键字;
2.对于每个后缀的前两(1+1)个字符进行一次排序,(将\(suf[i]\)的前两个字符\(S[i],S[i+1]\),看做一个整体进行排序,由于第一步已经的到了长度为1的子串的排名,这里就等价于将它们的排名进行合并后再排序),再得到它们的排名作为每一个后缀的第一关键字;
3.对于每个后缀的前三个(1+2)个字符进行依次排序,再得到它们的排名作为每一个后缀的第一关键字;
4.对于每个后缀的前五个(1+4)个字符进行依次排序,
······
直到所有排名都互不相同;
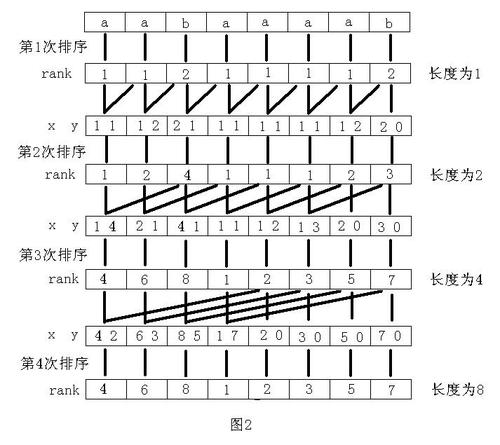
看图片更好理解,就是一个不停排序合并再排序的过程,每次合并时都能保证是上一步已经解决的问题,且对于每一个后缀都能不重不漏地包含所有字符,因此这样的排序效果上是等价于暴力基数排序的;
又由于合并长度是倍增实现的,所以最多进行\(log_2n\)次排序,而每次排序都使用位数为\(2\)的基数排序,就能使算法时间复杂度维持在\(O(nlogn)\)级别;
这部分的的代码
#include<bits/stdc++.h>
#define ll long long
#define mp make_pair
using namespace std;
const int N=100005;
char c[N];
int n,m=127;//m是值域的初始大小
int tub[N];//桶
int fk[N],psk[N];//注意!!!fk(first key)是某个位置的一关键字
//而psk(pos of second key)是 排名为i的二关键字所在的位置
int sa[N],height[N],rk[N];
//ll ans;
inline int read()
{
int x=0,fl=1;char st=getchar();
while(st<'0'||st>'9'){ if(st=='-')fl=-1; st=getchar();}
while(st>='0'&&st<='9') x=x*10+st-'0',st=getchar();
return x*fl;
}
inline void rsort()//基数排序
{
for(int i=1;i<=m;i++) tub[i]=0;//清空桶
for(int i=1;i<=n;i++) ++tub[fk[i]];//将第一关键字加入桶中
for(int i=1;i<=m;i++) tub[i]+=tub[i-1];//求桶的前缀和,得到一关键字的排名
for(int i=n;i>=1;i--) sa[tub[fk[psk[i]]]--]=psk[i];//按照从后到前的顺序,依据二关键字的排名得到目前的sa
}
inline void SA()
{
for(int i=1;i<=n;i++) fk[i]=c[i],psk[i]=i; //初始
rsort();//第一次排序
for(int k=1;k<=n;k<<=1)//合并的长度
{
int cnt=0;
for(int i=n-k+1;i<=n;i++) psk[++cnt]=i;//这一部分位置是没有能与其合并的 ,其二关键字应是最小的
for(int i=1;i<=n;i++)
if(sa[i]>k) psk[++cnt]=sa[i]-k; //这里的sa[i]会被某个位置合并,这个位置是sa[i]-k
//这一部分的二关键字是按照顺序加入的
rsort();
swap(fk,psk);//将fp放到psk转存,方便得到下一次的一关键字
fk[sa[1]]=1;
cnt=1;
for(int i=2;i<=n;i++) //如果两个位置的一关键字和二关键字都相同,则排名不同,需要+1
fk[sa[i]]=(psk[sa[i]]==psk[sa[i-1]]&&psk[sa[i]+k]==psk[sa[i-1]+k])?cnt:++cnt;
if(cnt==n) break;//如果已经所有排名不同了就可以退出
m=cnt;//更新值域
}
}
int main()
{
n=read();
scanf("%s",c+1);
SA();
// get_height();
// ans=(ll) n*(n+1)/2;
// for(int i=1;i<=n;i++)
// ans-=height[rk[i]];
// printf("%lld",ans);
return 0;
}
height数组的求法
主要依靠一个性质:
\(height[rk[i]] ≥ height[rk[i-1]]-1\)
感性证明:
假设排在\(suf[i-1]\)前面的那个串是\(suf[k]\)它们的最长公共前缀长度为\(height[rk[i-1]]\);
\(suf[i]\)比\(suf[i-1]\)少了它的第一个字符,可得\(suf[i]\)与\(suf[k+1]\)的最长公共前缀是\(height[rk[i-1]]-1\);
但\(suf[i]\)与\(suf[k+1]\)在排序后不一定在一起(即\(height[rk[i]]\)不一定是它们的最长公共前缀),
可是就算不在一起,在排好序的后缀中\(suf[k+1]\)与\(suf[i]\)之间的后缀都一定满足,与\(suf[i]\)的最长公共前缀至少是\(height[rk[i-1]]-1\);
那么一定有\(height[rk[i]] ≥ height[rk[i-1]]-1\);
这样就可以得到一个\(O(n)\)的代码
inline void get_height()
{
int k=0;
for(int i=1;i<=n;++i) rk[sa[i]]=i;
for(int i=1;i<=n;++i) //i是位置不是排名
{
if(k)--k;//-1
int j=sa[rk[i]-1];//找到排名前一个的位置
while(j+k<=n&&i+k<=n&&c[i+k]==c[j+k])++k;//继续匹配
height[rk[i]]=k;
}
}
一些应用
询问任意两个后缀的lcp
可以得知\(suf[i]\)与\(suf[j]\)(\(rk[i]<rk[j]\))的\(lcp\)长度就是\(\min\limits_{k=rk[i]+1}^{rk[j]}height[k]\);
这就变成一个区间最小值的问题了;
本质不同的子串
串\(S\)的所有子串个数是\(n*(n+1)/2\);
串\(S\)的所有子串也可以由,所有后缀的前缀得来;
其中相同的有\(\sum height[i]\)个;
所以有:
两个串的最长公共子序列
\(Dp\)会超时的那种;
一个简单的做法是:
将两个串合并成一个串,并且中间用一个不会出现的字符隔开(如%),求出新串的后缀数组;
求出一个最大的\(height[i]\),满足\(sa[i]\)和\(sa[i-1]\)在不同的串里面;
这个做法可以推广到多个串的最长公共子序列,但时间也会增加;
出现次数大于等于k的最长子串
找出,长度为\(k-1\)的序列的\(height[]\)的最小值,的最大值;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号