gin框架（1）- 路由原理：trie和radix tree

1. 前言

本篇是对gin框架源码解析的第一篇，主要讲述gin的路由httprouter的原理：radix tree（压缩字典树）。

2. Trie(字典树)

　　在讲述radix tree之前，不得不简单提到radix tree的基础版本trie，又叫字典树，前缀匹配树(prefix tree)，适合存储key为string，且所有key含有大量公共前缀的map型数据结构，示例如下：

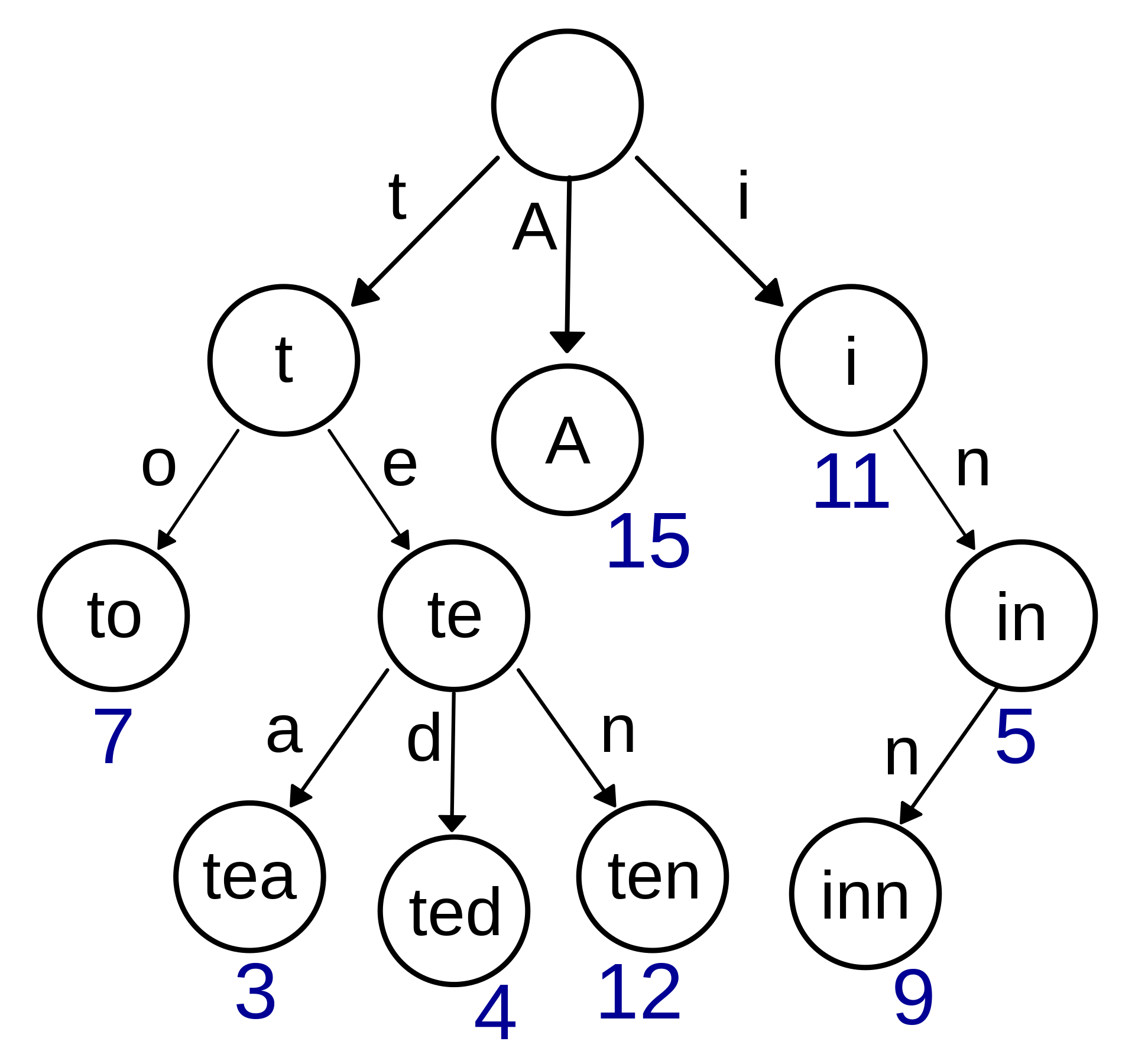
图1 trie示例(from wiki)

trie的讲述和应用，已经有很多珠玉在前，在此推荐Leetcode 208 实现Tire 和前缀树算法模板秒杀 5 道算法题 , 完成这两部分，基本就能对trie及其相关问题得心应手。在此主要介绍一些常见的trie的应用场景：

字符串排序：构造一颗trie，并且其每个节点的所有子节点的key顺序是按字典序进行排列的，那么按照前序遍历去访问这颗trie，就是有序的字符串。这样排序的时间复杂度和空间复杂度都比较低。

字符串匹配：KMP作为最著名的字符串匹配算法，用来判断一个长文本中是否包含某个特定的短文本字符串，其时间复杂度大致等于O(n)，n为长文本的字符数量。假设现在有一堆短文本字符串(m个短文本字符串)，需要找出所有在长文本中存在的短文本字符串（长文本的字符数量为n），应该如何实现？一个简单的思路是对每个短文本字符串调用KMP算法，那么时间复杂度即为O(n*m)。但是如果采用trie来实现匹配，其时间复杂度应该介于O(n)和O(n*m)之间（具体取决于所有短文本字符串的公共前缀的数量）。

索引存储：本质上还是利用trie前缀匹配的特性，在相应的子节点存储上对应数据的存储位置，当用户输入查询条件时，可以快速查找符合用户输入前缀的相应数据，常用于搜索引擎。

3. radix tree(压缩字典树)

　　压缩字典树是字典树的优化版本，字典树每个节点上只存储一个字符；而压缩字典树每个节点上存储着一个或多个字符；父节点上存储的字符为所有子节点的公共前缀。示例如下：

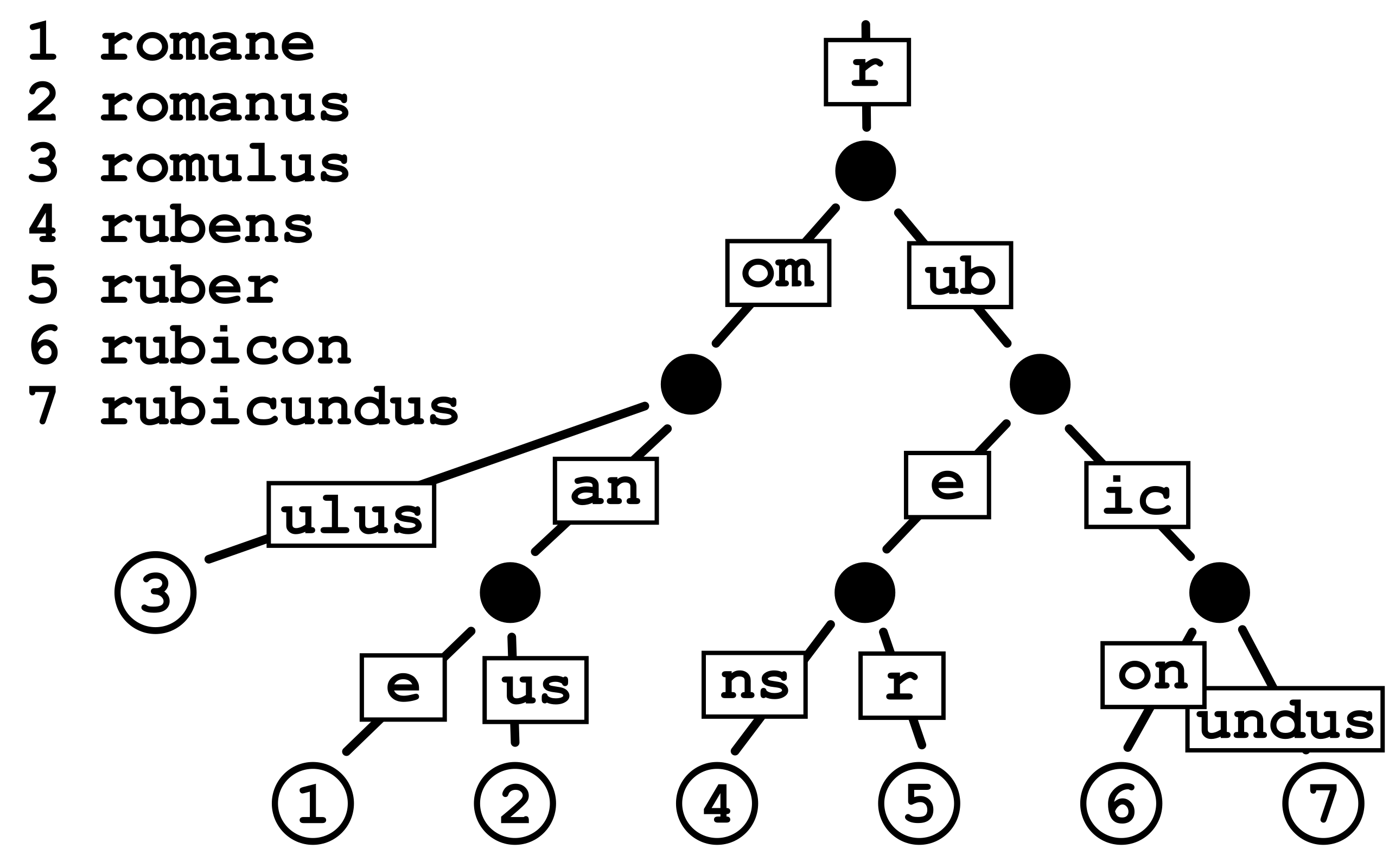
图2 radix tree示例（from wiki）

对于有大量公共前缀的多个字符串，采用radix tree可以显著减少节点数量，加快匹配速度。而URL路由就存在大量的公共前缀，因此很适合用radix tree来存储路由信息。

3.1 radix tree结构定义

　　在维基百科中，把数据radix_tree分成了“节点”和“边”两种数据结构，在“边”里存储路径，如上图所示。但是实际开发时，直接用节点一种数据结构即可。一个radix tree节点通常包含以下数据：

class Node:
    def __init__(self, path, has_value=False, value='', children=None):
        self.path = path # 该节点存储的路径，也可以增加一个数据，存储从根到该节点的完整路径
        self.has_value = has_value # 是否有存储数据
        self.value = value  # 叶节点的数据
        if children == None:  # 注意此处的默认值初始化方式
            self.children = [] 
        else:
            self.children = children  # 该节点的所有子节点，子节点也为Node类型

然后一颗radix tree级又用以上节点组成的一颗树。

class RadixTree:
    def __init__(self):
        self.root = Node(path = '')  # 声明一个根节点，根节点不包含任何数据

3.2 查找操作

查找时，从根节点出发，伪代码如下：

class RadixTree:
    def lookup(path):
        node = self.root # 从根节点开始
        1. for循环遍历node的每一个子节点child，查看child.path和path:
            if child.path == path and child.has_value:
                return True # 找到节点
            elif len(child.path) < path and child.path == path[:len(child.path)]:
                # 匹配上前缀，继续查询该节点的子节点
                node = child，path = path[len(child.path):]，并回到步骤1
            else:
                # 没匹配上，继续下一个节点
                continue
        2. for循环结束，还没有找到匹配的节点，返回False

为了后续的删除操作（删除操作需要找到path对应的节点，不论该节点是叶子节点还是路径节点），对查找操作稍微修改一下，对应的python代码如下：

class RadixTree:
    def find_node(self, path):
        """返回值为has_node(True or False), node(None if not exist)
        注：即使返回了node，也不代表该node有value值，可能该node只是一个路径节点
        """
        if path == '':
            return True, self.root
        node = self.root
        index = 0
        while index < len(node.children):
            child = node.children[index]
            if child.path == path:
                return True, child
            elif len(child.path) < len(path) and child.path == path[:len(child.path)]:
                node = child
                path = path[len(child.path):] # 截断公共前缀的部分
                index = 0
                continue
            else:
                index += 1
        return False, None

3.3 插入操作

插入节点时，节点的全路径为path，首先找到radix tree上跟该path有最长公共前缀的节点longes_prex_node，查看longes_prex_node的全路径longes_prex_node.path和path的关系，如果longes_prex_node.path=path，说明存在该节点，直接在该节点插入值即可；如果longes_prex_node有某个子节点child的path与new_path=path[len(longes_prex_node.path):]有公共前缀，则以公共前缀单独分裂成一个节点替换掉该child，并将剩下的路径生成一个新的节点作为该child的子节点；如果longes_prex_node没有子节点的path与new_path=path[len(longes_prex_node.path):]有公共前缀，则直接将剩下的路径作为一个子节点，添加到longes_prex_node的末尾即可。常见的三种插入情况如下：

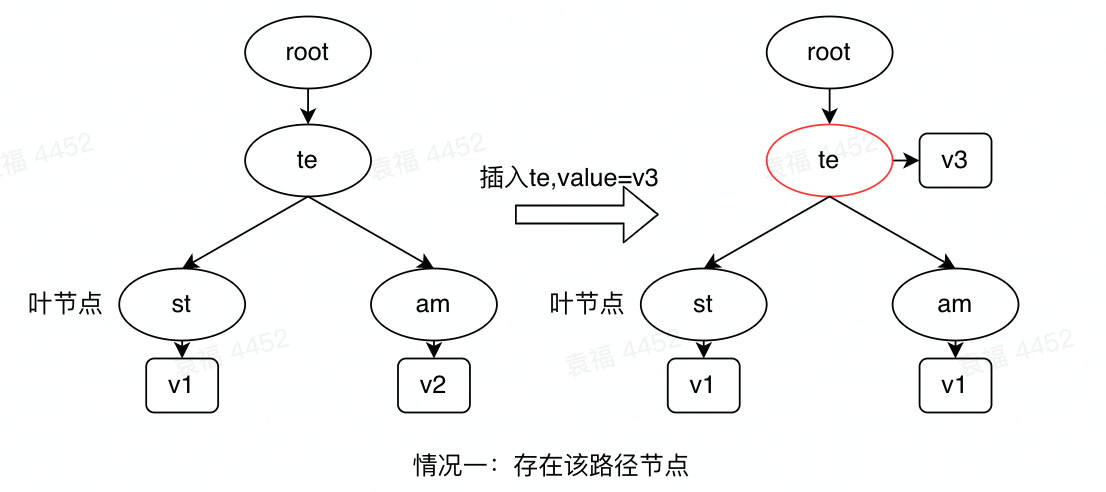
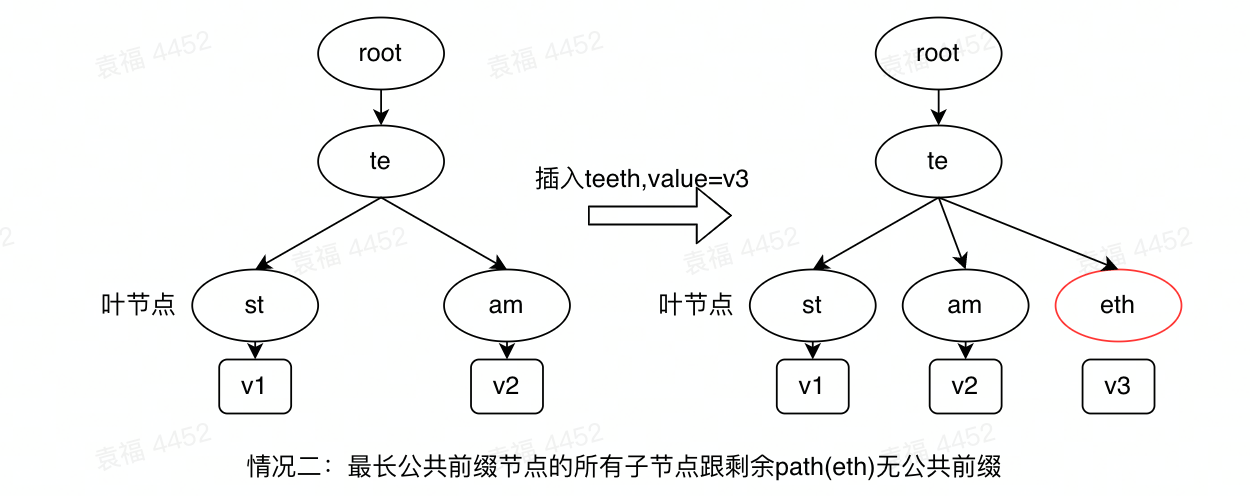
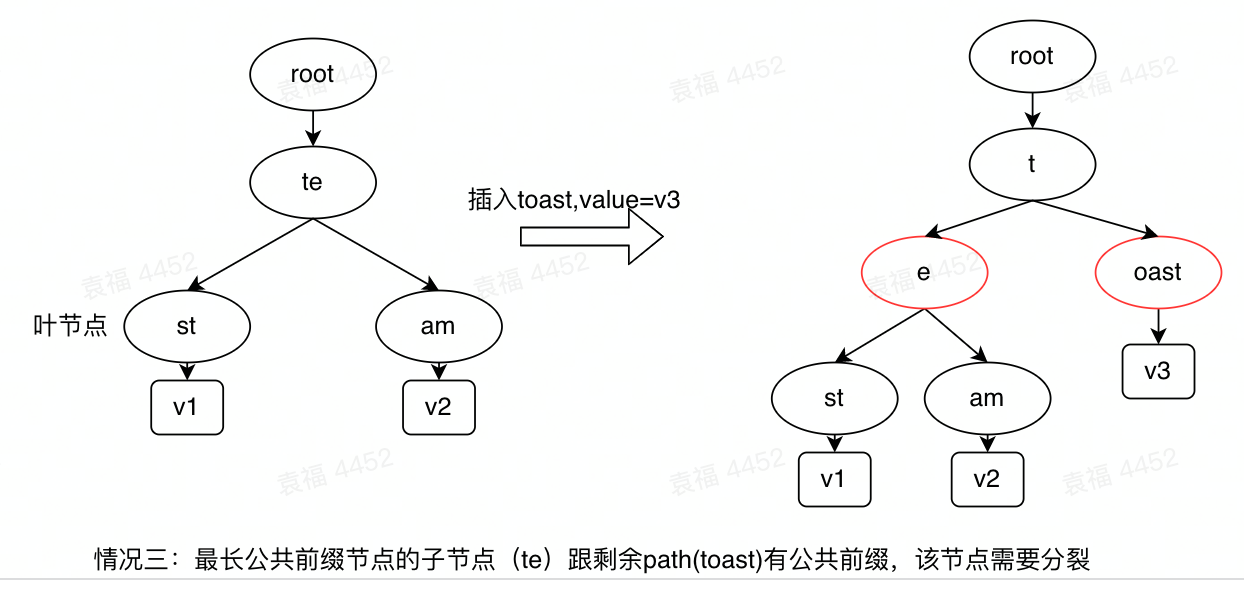
图3 插入操作的常见情况

可见插入需要找到最长公共前缀节点（需要该辅助方法），然后执行插入操作，具体的代码如下：

class RadixTree:
    def find_longest_prex_node(self, path):
        """返回值为node(最长公共前缀节点), prex(最长公共前缀)
        """
        if path == '':
            raise Exception('path cannot be empty')
        node = self.root
        index = 0
        common_prex = '' # 记录公共前缀
        while index < len(node.children):
            child = node.children[index]
            if child.path == path:
                common_prex = path
                return child, common_prex
            elif len(child.path) < len(path) and child.path == path[:len(child.path)]:
                common_prex += child.path
                node = child
                index = 0
                continue
            else:
                index += 1
        return node, common_prex
        
    def insert(self, path, value):
        common_prex_node, common_prex = self.find_longest_prex_node(path)
        if common_prex == path:
            # 已经存在该节点，直接更新值
            common_prex_node.has_value = True
            common_prex_node.value = value
        path = path[len(common_prex):] # 剩余path
        for idx, child in enumerate(common_prex_node.children):
            if child.path[0] == path[0]:
                # 有公共前缀，把公共前缀作为一个单独的子节点
                i = 0
                while i < len(child.path) and i < len(path) and child.path[i] == path[i]:
                    i += 1
                new_child = Node(child.path[:i]) # 新的child
                grandson = Node(child.path[i:], has_value=child.has_value, value=child.value, children=child.children) #继承现有child的所有成员
                new_child.children.append(grandson)
                new_child.children.append(Node(path[i:], has_value=True, value=value)) # 要插入的值的位置
                common_prex_node.children[idx] = new_child
                return
        # 遍历完还没有返回结果，说明没有跟common_prex_node的所有child没有公共前缀
        node = Node(path, has_value=True, value=value)
        common_prex_node.children.append(node)
        return

`3.4 删除操作`

删除操作首先是找到待删除的节点node，然后分三种情况：

如果该节点没有children，则直接移除该节点；此时如果该节点父节点只剩下一个孩子，需要将父节点和父节点剩下的一个孩子合并；

如果该节点只有一个children，则node.path = node.path+node.children[0].path(跟其孩子节点的path merge), 然后node.value = node.children[0].value

如果该节点有多个children，则直接将其变成路径节点即可（node.has_value=False, node.value=null）

所以要删除，首先要找到对应的节点，因此查找函数除了返回True or False之外；如果返回True，还需要返回该节点，方便删除操作使用。

对应的python代码如下：

class RadixTree:
    def delete(self, path):
        has_node, node = self.find_node(path)
        if not has_node or node.has_value == False:
            return
        if len(node.children) == 0:
            # 直接删除该节点，需要找到其父节点
            _, parent_node = self.find_node(path[:len(path)-len(node.path)])
            idx = 0
            while idx < len(parent_node.children):
                if parent_node.children[idx].path == node.path:
                    break
                idx += 1
            if len(parent_node.children) == 2:
                # 说明移除该节点之后只剩下一个节点了
                parent_node.path += parent_node.children[1-idx].path
                parent_node.has_value = parent_node.children[1-idx].has_value
                parent_node.value = parent_node.children[1-idx].value
                parent_node.children = parent_node.children[1-idx].children
                return
            else:
                parent_node.children = parent_node.children[:idx] + parent_node.children[idx+1:]
                return
        elif len(node.children) == 1:
            node.path = node.path + node.children[0].path
            node.has_value = node.children[0].has_value
            node.value = node.children[0].value
            node.children = node.children[0].children
            return
        else:
            node.has_value = False
            node.value = ''

3.5 遍历操作

为了检查以上插入，删除，查找的正确性，写了一个遍历RadixTree的辅助函数：

class RadixTree:
    def traverse(self):
        full_path = ''
        self.DFS(self.root, full_path)

    def DFS(self, node, full_path):
        if node == None or len(node.children) == 0:
            return
        for i in range(len(node.children)):
            child = node.children[i]
            full_path += child.path
            print('node full path: {}, node path: {}, has_value: {}, value: {}'.format(full_path, child.path, child.has_value, child.value))
            self.DFS(child, full_path)
            full_path = full_path[:len(full_path)-len(child.path)]

4. httprouter概述

gin的路由注册采用的是httprouter。httprouter是基于radix tree实现的前缀匹配。httprouter在实现radix tree时增加了一些针对url的优化：

（1）每一种http方法一个 radix tree，这样可以提高匹配效率；

（2）提供了通配符 ":" 和 "*"，其中 ":"+参数名称表示路径参数，比如 GET /template/:user_id，其中 ":user_id" 就是一个路径参数，访问时用户输入url： /template/12345，则user_id=12345。"*"+参数名称为匹配所有参数，结构只能为 .../.../.../*param_name，"*" 只能作为结尾参数。

posted @ 2022-10-21 10:47 晨枫1 阅读(816) 评论(0) 编辑收藏举报

刷新页面返回顶部

晨枫1