线性模型

 一.线性模型（linear model）

其中w直观表达了各属性在预测中的重要性

 

二.线性回归模型

1.线性回归，下面 x 的第一个下标表示第几个样例，第二个下标表示该样例的第几个特征,也有上下标的写法，上标表示第几个样例，下标表示第几个特征

2.一元线性回归：仅考虑一个特征，即输入属性的数目只有一个，下面的 x_i 表示仅有一个特征时样例的输入值，即一维，即w为一个数，xi的下标i表示第几个样本

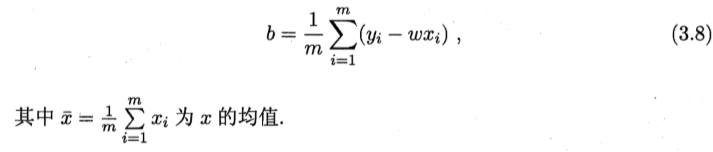
也就是说，对于一元线性回归，根据已有的数据集以及（3.7）和（3.8）直接可以构造出一元线性回归模型

 

3.多元线性回归：含有多个特征，多维，w为向量，它的个数对应样本的特征数

 

 

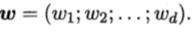
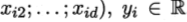
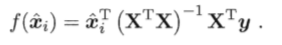
4.多项式回归

背景：很多情况下，数据的分布都是非线性的，因此对线性模型进行改进，采用多项式函数对数据进行拟合非线性数据，这是一种非线性回归模型

定理：对于给定的M个点，我们可以用一个M-1次的函数去完美地经过这个点集

优点：增强拟合能力和模型的容量

缺点：增加模型复杂度，易过拟合

解决：多项式回归问题可以通过变量转换化为多元线性回归问题来解决，比如x²换成x2

 

5.对数线性回归：将指数形式的真实值，取对数，使数据分布呈现线性

 

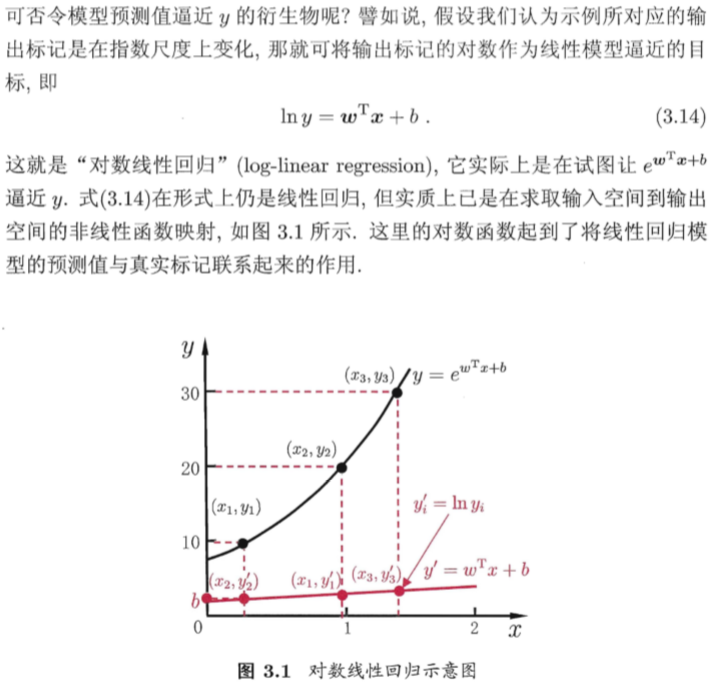
广义线性模型：找一个单调可微函数将分类任务的真实标记与线性回归模型的预测值联系起来

 

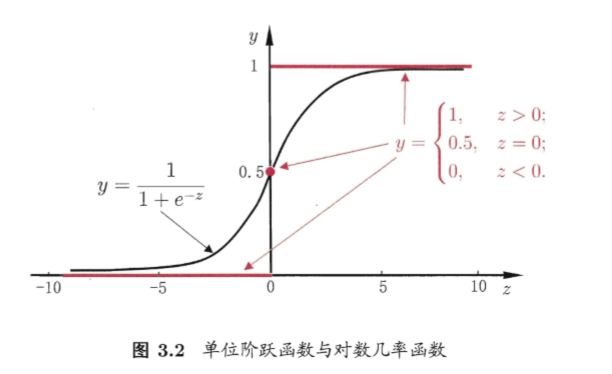
三.对数几率回归（sigmoid 函数）（logistic 回归）：实际是一种分类学习方法，因为预测值是离散的0或1

做法：对于分类任务，使损失函数小的时候预测准确 即单个样本预测值和输出值一致

线性回归不适用于分类，因为最小二乘损失函数，会导致损失函数多次弯曲，不再变为凸函数

对数几率回归优点：1.直接对分类可能性建模，无需假设数据分布；2.不仅预测出了类别，还得到近似概率预测，3，对数几率函数是任意阶可导凸函数，可求得最优解

（1）对于二分类任务，预测值为0/1，输出值在（0,1）之间，因此我们只需将线性回归模型产生的预测实值转换为0/1值

 

 

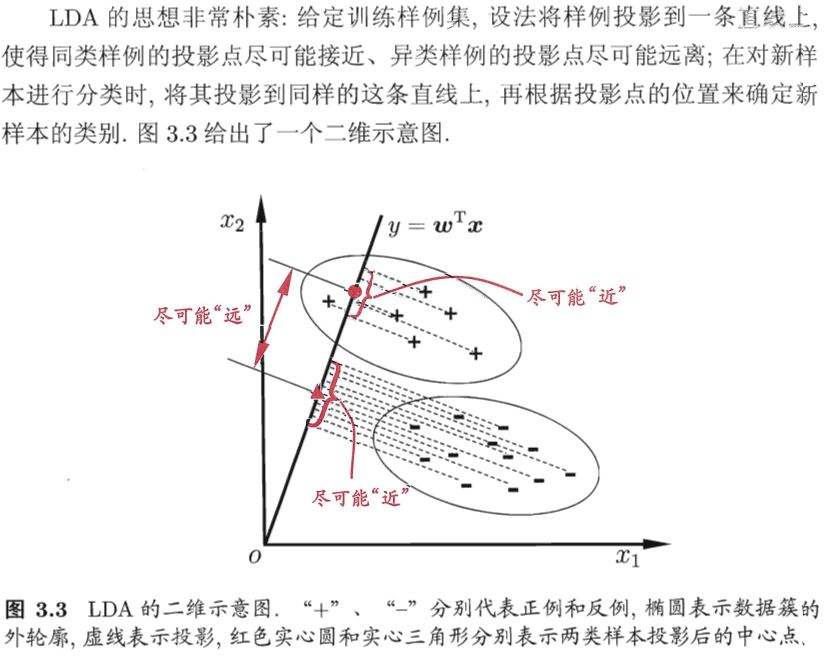
四.线性判别分析（LDA）(Linear Discriminate Analysis)

 

 

 

五.多分类学习

1.多元逻辑回归：从隐含变量出发，推导各个类别的概率

（1）定义k个隐含变量模型，对于同一样本，定义不同的类别会有不同的参数
（2）个体属于某个类别，
（3）推导各个类别的类别概率分布
（4）定义模型的似然函数
（5）利用最大似然估计法估计参数

2.把一个多分类问题转为多个二分类问题，将多维降维到二维

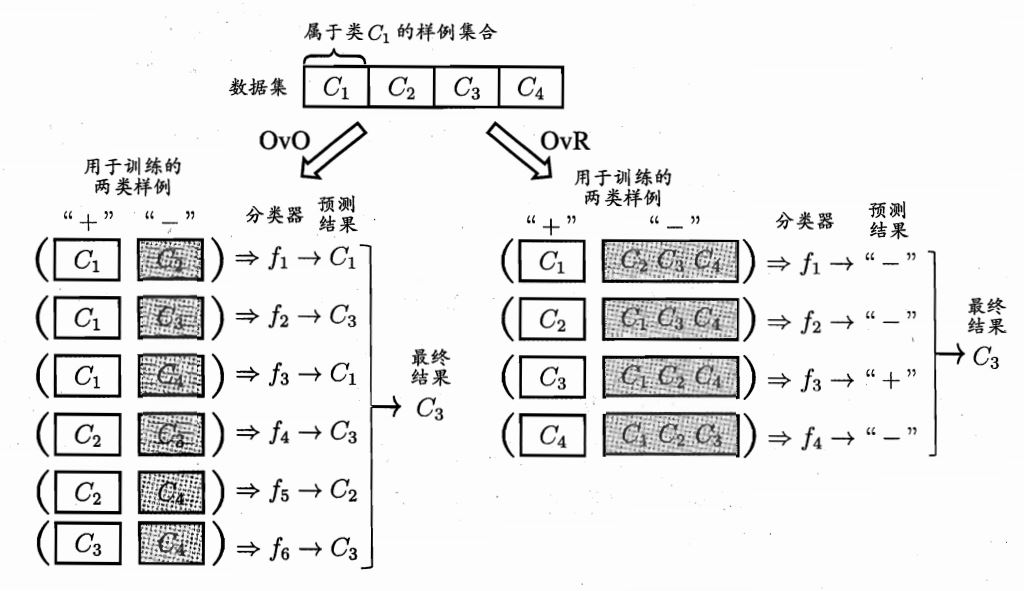
拆分策略：（1）一对一：将类别两两配对，就有N(N-1)/2=1+2+3+...+（n-1)个二分任务,产生N(N-1)/2个结果，把预测的最多的类别作为最终分类结果

（2）一对多：训练N个分类器，每次将一个作为+例，其他为反例，若只有一个结果为+，则为那类，如果有多个为+，则选择置信度最大的类别标记

（3）多对多：每次将若干类作为+，若干类作为-，作M次训练，得到M个分类器，再根据某种规则判别类别

 

 

 

六.

import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

# 线性模型

#####################################################
# 创建随机数据并保存
def generate_data():
    num_points = 300
    data = pd.DataFrame(columns=['X', 'Y'])
    for i in range(num_points):
        x = np.random.normal(0.0, 0.5)  # 正太分布（均值，标准差）,生成一个正太分布的随机数
        y = x * 2 + 3 + np.random.normal(0.0, 0.3)  # 添加一个服从正太分布的误差
        data.loc[len(data)] = {'X': round(x,3), 'Y': round(y,3)}
    plt.figure()
    plt.scatter(data['X'], data['Y'])
    plt.show()
    data.to_csv('./datas/regression.csv')
    return data
generate_data()
#################################################
# 1.读取数据集，并划分训练集+验证集+测试集
data = pd.read_csv('./datas/regression.csv')
train_sample_num = int(round(len(data.X) * 0.6, 0))
validation_sample_num = int(round(len(data.X) * 0.2, 0))
test_sample_num = int(round(len(data.X) * 0.2, 0))

x_train = data.X.iloc[0:train_sample_num].to_numpy()
y_train = data.Y.iloc[0:train_sample_num].to_numpy()
x_validation = data.X.iloc[train_sample_num:train_sample_num + validation_sample_num].to_numpy()
y_validation = data.Y.iloc[train_sample_num:train_sample_num + validation_sample_num].to_numpy()
x_test = data.X.iloc[train_sample_num + validation_sample_num:
                     train_sample_num + validation_sample_num + test_sample_num].to_numpy()
y_test = data.Y.iloc[train_sample_num + validation_sample_num:
                     train_sample_num + validation_sample_num + test_sample_num].to_numpy()

#  2.创建模型，设定相关参数，
model = tf.keras.Sequential()  # 顺序模型)
model.add(tf.keras.layers.Dense(1, input_shape=(1,), activation=tf.keras.activations.linear))  # 全连接一层，激活函数为线性，即不做任何改变
print(model.summary())

#  3.模型编译以及训练
model.compile(optimizer=tf.keras.optimizers.SGD(),  # 随机梯度下降法
              loss=tf.keras.losses.mean_squared_error,  # 均方误差mean squared error
              metrics=[tf.keras.metrics.mean_absolute_error])  # 平均绝对误差mean absolute error

model_history = model.fit(x_train, y_train, batch_size=60, epochs=9,
                          validation_data=(x_validation, y_validation))


print(model_history.history)
plt.plot(model_history.history['loss'])

test_result = model.evaluate(x_test, y_test)
print(dict(zip(model.metrics_names, test_result)))

plt.show()

 

七