20172313 2018-2019-1 《程序设计与数据结构》第八周学习总结
20172313 2018-2019-1 《程序设计与数据结构》第八周学习总结
教材学习内容总结
- 堆
- 堆(heap)就是具有两个附加属性的一棵二叉树。特点:①最小堆是一棵完全树。②最小堆对每一结点,它小于或等于其左孩子和右孩子。(最大堆的结点大于或等于它的左右孩子)
- HeapADT的UML描述。
| 操作 | 说明 |
|---|---|
| addElement | 将给定元素添加到该堆中 |
| removeMin | 删除堆的最小元素 |
| findMin | 返回一个指向堆中最小元素的引用 |
- 最小堆结点的子树同样是最小堆,两个不同的最小堆可能包含数据相同。
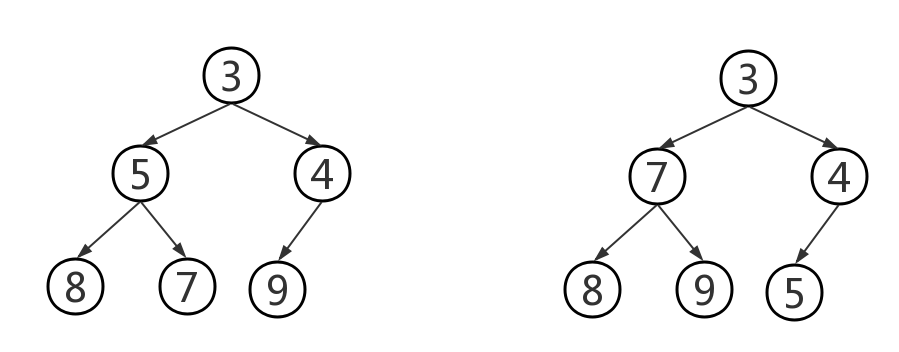
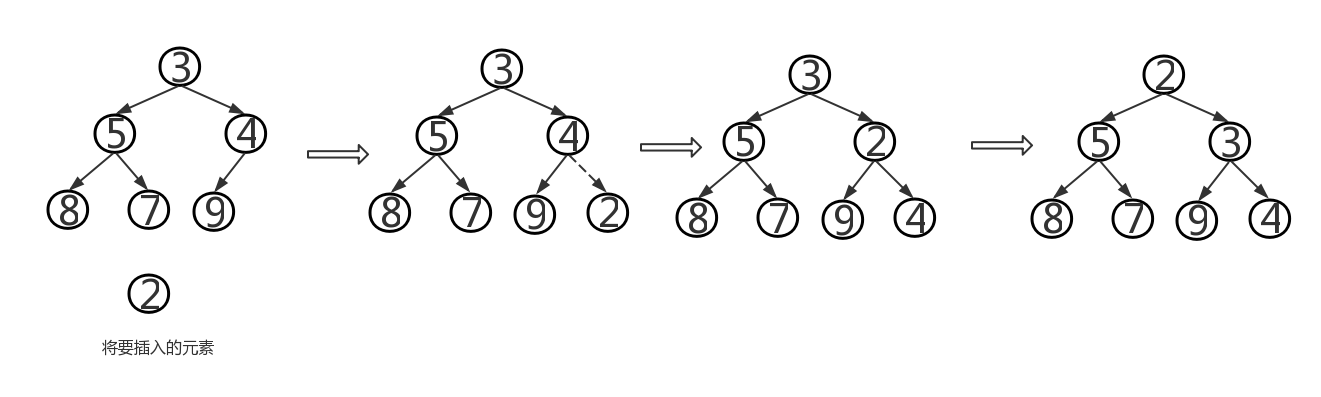
- addElement操作:将给定的元素添加到堆中的恰当位置,由堆的定义可知,这里的元素要能够进行比较,所以必须是Comparable类型的,如果不是,则会抛出异常。如果一棵二叉树是平衡的,即所有叶子都位于h或h-1层。其中h为log2^n,且n是树中的元素数目,因为堆是一棵完全树,所以h层的叶子都位于该树的左边。所以插入结点时只有两种情况:①h层的最后一个位置。②h+1层的第一个位置。将新元素添加至堆的末尾后,保持树是完全树,将该元素向根的地方移动,将它与父结点对换,直到其中的元素大小关系满足要求为止。
- 在链表实现中,添加元素时首先要确定插入结点的双亲。最坏的一种情况是从右下的最后一个叶子节点一直遍历到根,在遍历到堆的左下结点 。该过程的时间复杂度为2logn。下一步是插入节点(简单的赋值,这里的时间复杂度为O(1))。最后一步是将这棵树进行重新排序。因为从根到结点的路径长度为logn,所以最多需要进行logn此操作。因此使用链表实现时操作的复杂度为2*logn+1+logn。即O(logn)
- 在数组实现中,添加元素时并不需要确定新结点双亲的步骤,但是,其他两个步骤与链表实现的一样。因此,数组实现的addElement操作的时间复杂度为1+logn或O(logn)。虽然这两者实现的复杂度相同,但数组实现的效率更高一些。
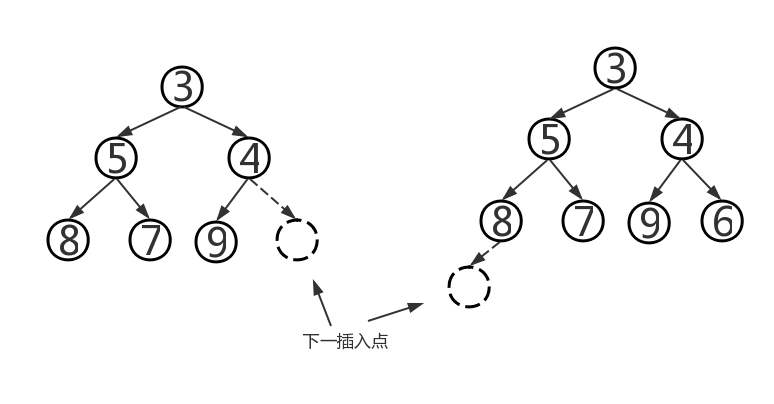
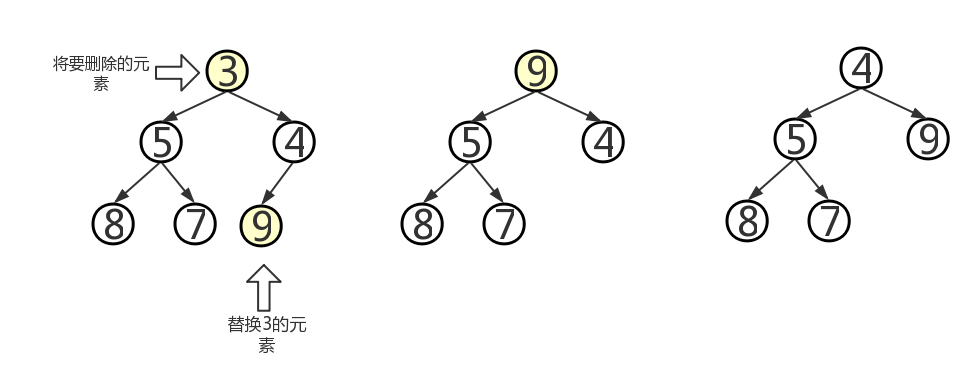
- removeMin操作:根据堆的定义可知,堆中的最小元素位于根结点,这时我们要把该树储存在最末一片叶子中的元素移到根结点处,一旦元素移动,就要对该树进行重新排序:将该新根元素与较小的那个孩子进行比较,如果孩子更小则将它们互换。从上至下继续这一过程,直到该元素要么变成叶子结点,要么比它的两个孩子都小。
- 在链表实现中,removeMin必须删除根元素,并用最后一个结点的元素来替换它(简单的赋值,时间复杂度为O(1))。下面要对该树进行重新排序,因为该树原先是一个堆,所以只需要跟较小的一边进行比较排序。因为从根到叶子的最大路径长度为logn,因此该步骤的时间复杂度为O(logn)。到此时,这棵树已经完成了,但在实际进行的过程中,为了继续完成接下来的操作,我们还要找到新的最末结点,最坏的情况是进行丛叶子到根的遍历,然后再从根往下到另一叶子的遍历。因此,该步骤的时间复杂度为2logn。于是removeMin操作最后的时间复杂度为2logn+logn+1,即O(logn)。
- 在数组实现中,removeMin也像链表实现的那样,只不过它不需要确定最新的最末结点。因此,数组实现的removeMin操作的复杂度为logn+1。即O(logn)。
- findMin操作:findMin操作较为简单,由堆的定义可知,直接返回根结点的元素即可。
- 堆和二叉排序树的区别:
- ①堆是一棵完全二叉树,二叉排序树不一定是完全二叉树;
- ②在二叉排序树中,某结点的右孩子结点的值一定大于该结点的左孩子结点的值,在堆中却不一定;
- ③在二叉排序树中,最小值结点是最左下结点,最大值结点是最右下结点。在堆中却不一定;
- 使用堆:优先级队列:按照优先级从大到小进行排序,具有相同优先级的按照先进先出来进行排序。虽然最小堆根本就不是一个队列,但是它却提供了一个高效的优先级队列实现。
| 操作 | 说明 |
|---|---|
| addElement | 往树中添加一个元素 |
| removeElement | 从树中删除一个元素 |
| removeAllOccurrences | 从树中删除所指定元素的任何存在 |
| removeMin | 删除树中的最小元素 |
| removeMax | 删除树中的最大元素 |
| findMin | 返回一个指向树中最小元素的引用 |
| findMax | 返回一个指向树中最大元素的引用 |
- 用链表实现二叉查找树:每个BinaryTreeNode对象要维护一个指向结点所存储元素的引用,另外还要维护指向结点的每个孩子的引用。
教材学习中的问题和解决过程
- 问题一:在使用数组实现最小堆时,如果要进行removeMin操作需要把根元素删去,把“count-1”处的元素放到索引为0的地方,那么“count-1”处的元素不是还放在原位吗?书上并没有对该位置进行任何操作。
- 问题一解决方案:当时看到这里的时候,我认为是删除元素时就不对“count-1”处的元素进行操作,因为删除元素后count变量会自减,到时候遍历的时候只遍历到count的位置,这个问题也就先放到这里了。但是当我做到pp12_8时却发现不是这样。当我删除了最小元素后,在遍历的时候依旧会把最后一个元素打印。如下图所示
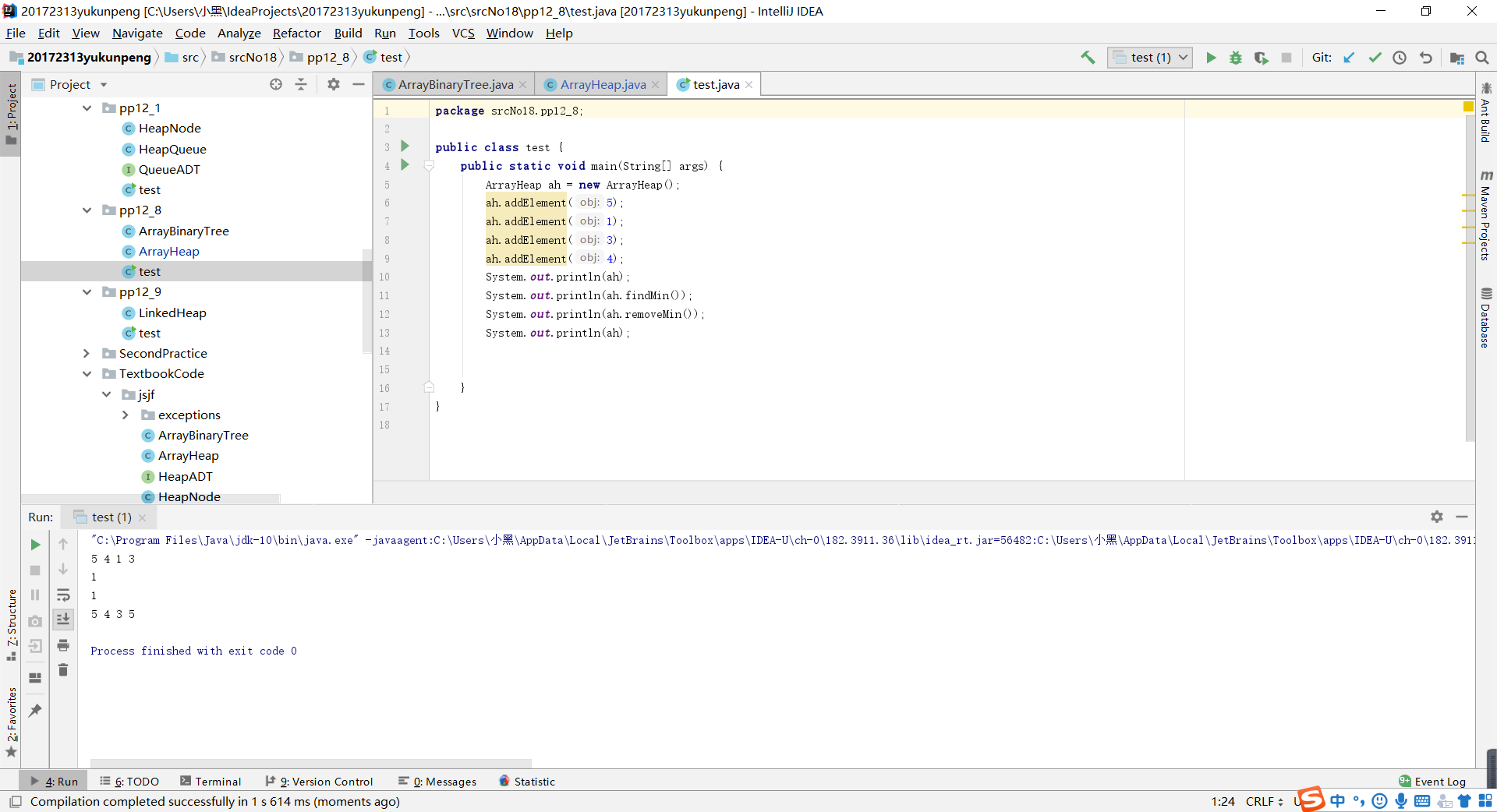
我们可以很清楚的看到,5作为最后一个元素并没有被删除,仍然会被打印,由于ArrayHeap继承的是ARRayBinaryTree类,我又查看了ArrayBinaryTree中的遍历方法。
public String toString()
{
ArrayUnorderedList<T> tempList = new ArrayUnorderedList<T>();
inOrder(0, tempList);
return tempList.toString();
}
使用数组实现堆时使用中序遍历,打印数组中不为空的所有元素,所以在这里我觉得书上的内容是有问题的,在ArrayHeap的removeMin()方法中应该添加吧“count-1”处的元素清空的操作。这样问题就得以解决了。
public T removeMin() throws EmptyCollectionException
{
if (isEmpty())
throw new EmptyCollectionException("ArrayHeap");
T minElement = tree[0];
tree[0] = tree[count-1];
tree[count-1] = null;(新添加的操作)
heapifyRemove();
count--;
modCount--;
return minElement;
}
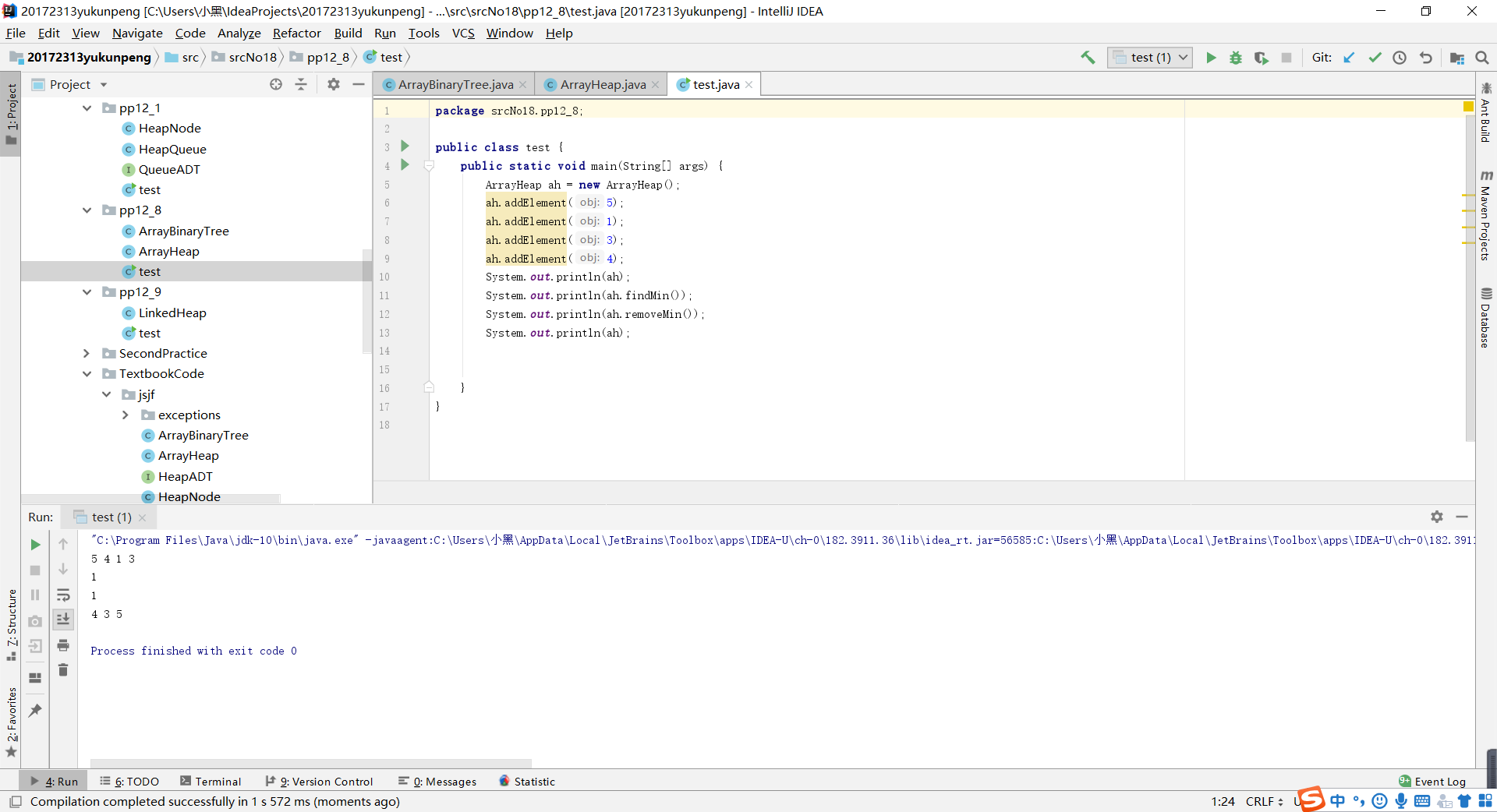
- 问题二:在看链表实现堆时,有这样一段话“heapifyAdd方法并没有执行双亲与孩子的完整互换。它只是把双亲元素往下平移到正确的插入点,然后把新值赋给该物质。这并没有真正改变算法的复杂度,即使执行完整的元素互换,其复杂度也是O(logn)。但是,它的确提高了效率,因为它减少了左堆的每一层上要执行的赋值次数。”我对于这段话不是很理解。
- 问题一解决方案:我是这样理解的,先用temp储存插入节点的元素,与父结点内储存的元素进行比较,如果父结点的元素大于temp,则把父结点的元素赋给子结点。注意:此时并没有把temp的值赋给父结点,没有执行完整的元素互换。这时继续进行遍历,找到父结点的父结点,让父结点的父结点的元素与temp进行比较,重复以上步骤,直到根结点或有一结点的元素小于temp,这时,该结点的子结点就是新插入元素的位置,即把temp赋给它。由于没有进行完成的元素互换,效率自然也就提高了。
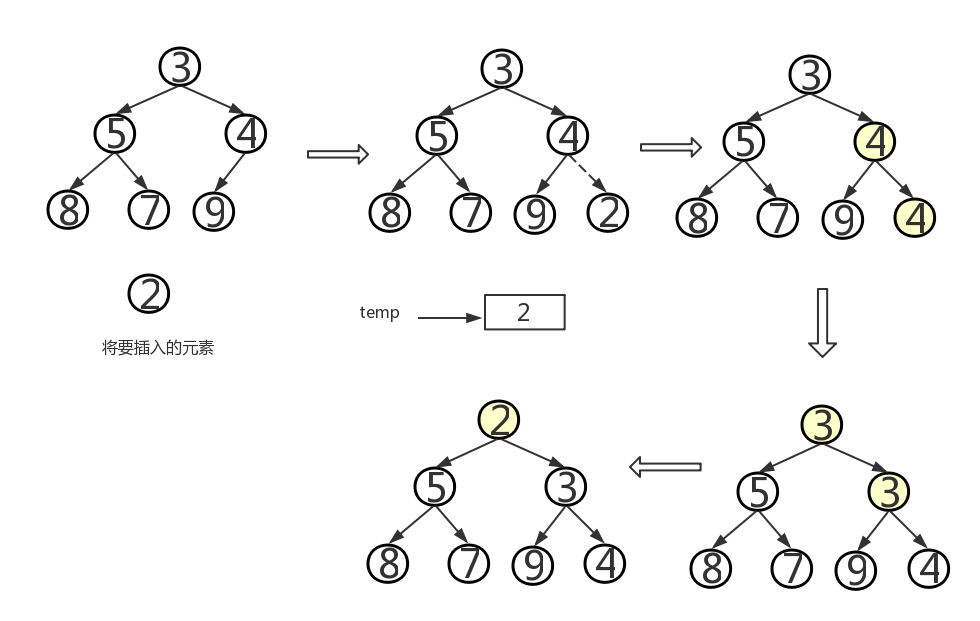
代码调试中的问题和解决过程
- 问题1:对使用数组实现堆中的removeMin操作的heapifyRemove方法不是特别理解。代码如下:
private void heapifyRemove()
{
T temp;
int node = 0;
int left = 1;
int right = 2;
int next;
if ((tree[left] == null) && (tree[right] == null))
next = count;
else if (tree[right] == null)
next = left;
else if (((Comparable)tree[left]).compareTo(tree[right]) < 0)
next = left;
else
next = right;
temp = tree[node];
while ((next < count) &&
(((Comparable)tree[next]).compareTo(temp) < 0))
{
tree[node] = tree[next];
node = next;
left = 2 * node + 1;
right = 2 * (node + 1);
if ((tree[left] == null) && (tree[right] == null))
next = count;
else if (tree[right] == null)
next = left;
else if (((Comparable)tree[left]).compareTo(tree[right]) < 0)
next = left;
else
next = right;
}
tree[node] = temp;
}
- 问题一解决方案:我们先来一行一行的逐步分析代码,我们知道此方法是用来对堆进行重新排序的。首先,判断删除最小元素后是否只剩下一个结点,如果是,则跳过后面判断和循环,将剩下的唯一元素设置为根结点。有前面的内容可知,对于每一结点,n的右孩子将位于素组的2(n+1)处,n的右孩子将位于数组的2(n+1)处。如果对于根结点来说,它没有右孩子或左孩子的元素小于右孩子的元素,则令next=left进入下一步的循环,如果它的右孩子的元素大于左孩子的元素。则令next=right进入下一步的循环。(注意:在判断结束后,temp= tree[node]的作用为保存此时根节点的元素向下遍历进行比较,最后赋值给通过循环找到的结点。)当进入循环以后,将根结点的元素与索引为next处的元素(左孩子或右孩子)进行比较,如果next处的元素比temp小,则令node(next的父结点)处元素为next。继续向下遍历,把next的值赋给node,并找到node的孩子的索引,令next重新指向node的孩子。当跳出循环时,node结点的位置即为temp的位置,完成排序。
代码托管

上周考试错题总结
- 错题1:What type does "compareTo" return?
A . int
B . String
C . boolean
D . char - 解析:这题错的实在是不应该,当时做的太快了,满脑子都想着compareTo用来比较两个对象之间的大小,返回一个boolean型的变量,却忘了是根据返回int值的大小来判断的。
- 错题2:Insertion sort is an algorithm that sorts a list of values by repetitively putting a particular value into its final, sorted, position.
A . true
B . false - 解析:概念题,插入排序通过反复地把某个元素插入到之前已排序的子列表中,实现元素的排序。
- 错题3:A binary search tree is a binary tree with the added property that the left child is greater than the parent, which is less than or equal to the right child.
A . True
B . Flase - 解析:概念题,做的时候理解错误,二叉查找树是一种含有附加属性的二叉树,即其左孩子小于父结点,而父结点又小于或等于右孩子。
- 错题4:One of the uses of trees is to provide simpler implementations of other collections.
A . True
B . Flase - 解析:这道题做的时候没有理解清楚题意。树的主要作用之意2是为其他集合提供高效的实现,而不是简单的实现。
结对及互评
- 博客中值得学习的或问题:
- 排版精美,对教材的总结细致,善于发现问题,对于问题研究得很细致,解答也很周全。
- 代码中值得学习的或问题:
- 代码写的很规范,思路很清晰,继续加油!
点评过的同学博客和代码
其他(感悟、思考等,可选)
相较与上周的折磨,这周的内容上可以说是友好了许多,经历了上周二插查找树的洗礼,这周的内容也只不过是新瓶装旧酒而已,没有什么太过新鲜的东西,主要是把一些关键的代码给弄明白,这一过程还是花了不少时间的。由于这周的实验也占用了不少时间,这周的学习内容其实并没有想象中那么轻松。希望自己能在以后的生活中继续努力,不断进步!
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 第一周 | 200/200 | 1/1 | 5/20 | |
| 第二周 | 981/1181 | 1/2 | 15/20 | |
| 第三周 | 1694/2875 | 1/3 | 15/35 | |
| 第四周 | 3129/6004 | 1/4 | 15/50 | |
| 第五周 | 1294/7298 | 1/5 | 15/65 | |
| 第六周 | 1426/8724 | 1/6 | 20/85 | |
| 第七周 | 2071/10795 | 1/7 | 20/105 | |
| 第八周 | 3393/14188 | 1/8 | 20/125 |
-
计划学习时间:20小时
-
实际学习时间:20小时

