同济高数（一）
数列的极限#
定义证明##
理解即是，不论你给定的正数有小，总能找到一个分界点第N项，在N向a逼近方向，存在无数个n项，使得x与a的距离小于这个正数 |这个不等式成立。那么就存在极限。
在证明数列极限存在时，我们只要找到使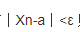
成立的条件，推出使
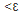成立的不等式，即可根据定义求解。
在求解证明时，若能知道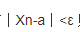小于某个量（这个量必须与n存在函数关系），那么当这个量小于ε时，就能证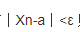成立。
极限的唯一性##
如果数列收敛，那么它的极限唯一。
求证：反证法。
极限的有界性##
如果数列收敛，那么数列一定收敛
求证：绝对值不等式性质
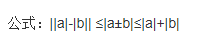
无界一定发散，有界不一定收敛
收敛数列的保号性##
理解即是,如果数列极限为a，假如a>0，那么在逼近到a之前，总存在一个分界点第N项，在N向a逼近的方向，存在无数个n项，使得函数值大于0。