gradient decsent & back propagation 阅读笔记

highlight：从生物学中获得的 insight。很多在实践中被证明有效的小 trick 的设计初衷都来自于人类对大脑有限的了解。

为什么是叫神经网络而不是别的名字？我们认为正数表示神经元之间的促进作用，负数表示神经元之间的抑制作用。

前置

• insight 洞见
  motivation 动机
  intuition 直觉
  approach 方法

• 牛顿迭代法

• objective function 目标函数
  loss function 损失函数

• parameter 参数
  hyperparameter 超参数

• train 训练
  validation 验证
  test 测试
  inference 推理

• 前向传播

formulated description of the pipeline?

train-validation-test

data 给了我们什么？每个 sample 前向传播能获得的 loss。
除了 data 中获得的信息，我们还可以利用神经网络在 computation 中生成的信息。古圣先贤们利用 “梯度” 这个信息训练出了非常出色的网络，于是相关的研究便围绕“梯度”展开

gradient descent

想利用梯度信息，一个蛮经典的策略是“牛顿迭代法”：

\(W_n = W_{n-1} -\eta \nabla W_{n-1}\)

\(\eta\) 被称为学习率.

• batch gradient descent ：整个 batch 的 loss 进行求平均。

  瓶颈：获得一次梯度信息，需要对数据集中所有数据进行前向传播。

• sgd：按照随机顺序计算 loss

  

  瓶颈：数据集中可能有离群值，导致梯度异常（噪声）

  于是我们想到可以让 sgd 和 batch gradient descent 进行 trade off：选 B 个样本做前向传播计算 loss，并反向传播：

• mini batch sgd

  选择 B（或者叫 batch size） 的依据有两类：

  1. 硬件：如果选择 \(B=2^k\) 或者说 32 64 128 等等，可以更好适配硬件提升效率

  2. 选择 B=1，会遭受噪声的影响。那么考虑在增大 B 的过程中，噪声的影响程度的变化。

     指标：考虑数据集中共有 \(N\) 个样本，如果使用 batch gradient descent，得到的是 loss（已求过平均值） 是 \(E\) ；每个样本的 loss 是 \(E_i\)，现在 \(\{E_i\}\) 的标准差是 \(\sigma\)。接下来将每 \(B\) 个 \(\{E_i\}\) 求平均，得到 \(\{E'_i\}\) ，那么 \(\{E'_i\}\) 的标准差是 \(\dfrac{\sigma}{\sqrt B}\)

  

mini batch sgd 是上面两种方法的 trade off。

这里有一个 minibatch sgd 训练效果的图片。

收敛性

你可能会疑惑为什么 \(H\) 是可对角化的。答案是“实对称矩阵可对角化”。

【总结前面】

Beyond SGD

这张图是 SGD 的收敛过程

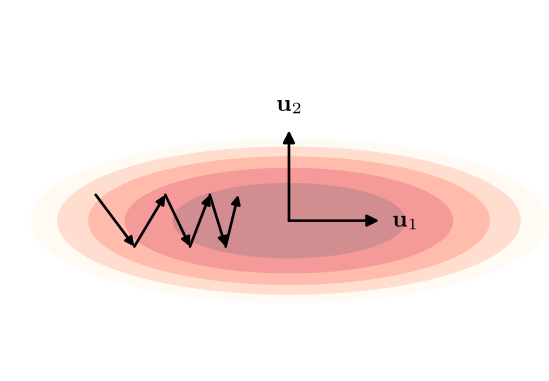
很费劲！问题出在了哪里？

答案：每次求梯度时只使用了当前点的梯度信息，忽略了之前走到的点的梯度

解决方案：momentum。

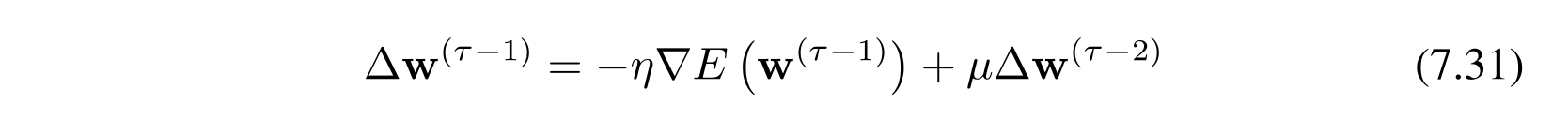
其中 \(\Delta w\) 表示参数的该变量，上标表示时间。右侧 \(\mu\) 是 hyper parameter。其中 \(\mu\in(0,1)\) 。以下是加了动量项后的收敛过程示意图

【指数衰减】是一个常见的优化技巧。另一个应用场景是RL reward accumulation。

learning rate strikes back

有很多人们拍脑袋想出来、并实践证明效果还不错的设置方法。总体都遵循一个 学习率在初期比较大，后面慢慢减小 的原则。

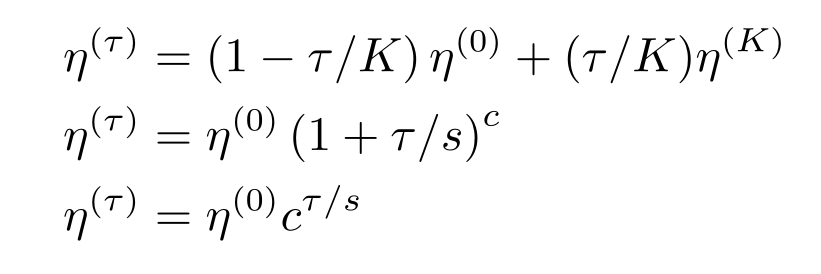
后来又有人提出了“预热阶段”，大概可以被下面这个曲线所描述

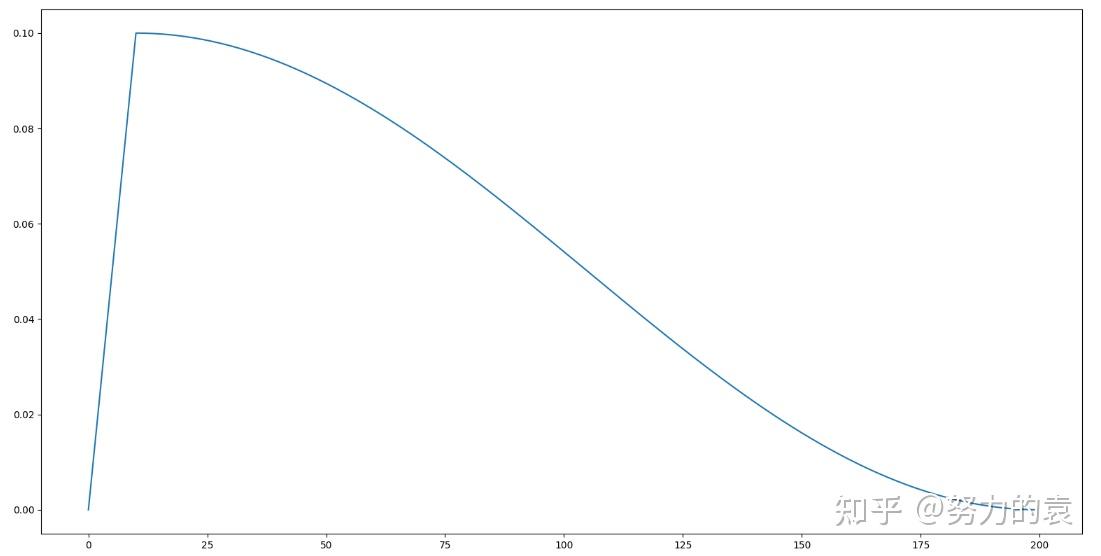
从这张图里可以看到，learning rate 最大的时候也只有 0.1，很多时候都在 0.02 以下。

学习率怎么都一样啊？

每个神经元的生长、老化过程也都不太一样啊。是不是每个参数设置不同的学习率，拟人效果更好一些！

adagrad：

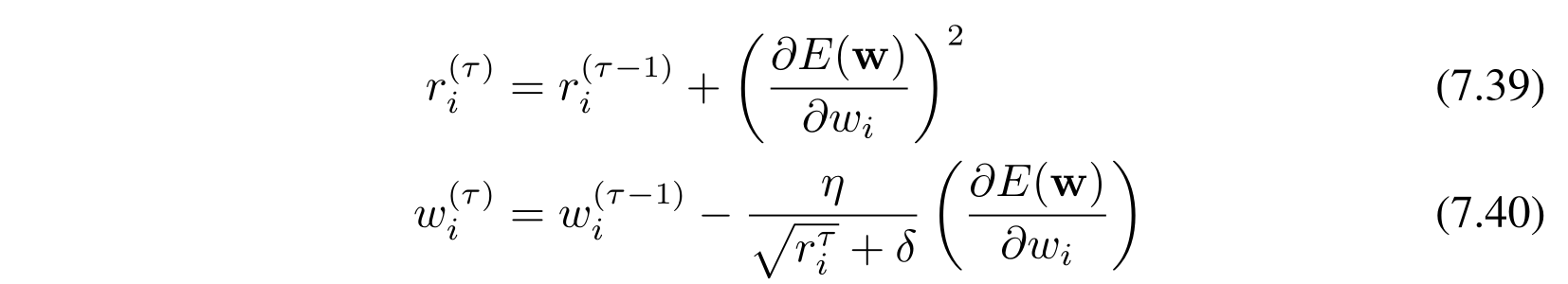
这里的 \(r_i\) 是每个神经元额外维护的变量，\(\delta\) 是为了防止分母为 0 的极小的数，例如 \(10^{-8}\)

adagrad 有一个比较明显的问题是在 \(r_i\) 越来越大，导致 \(\dfrac{\eta}{\sqrt{r_i} + \delta}\) 越来越小，在训练的后期无法更新参数。于是新科诺奖得主（不知道是不是从物理学上抄来的）把 \(r_i\) 做了一次指数衰减，得到了一种新的方法，叫 RMSprop：

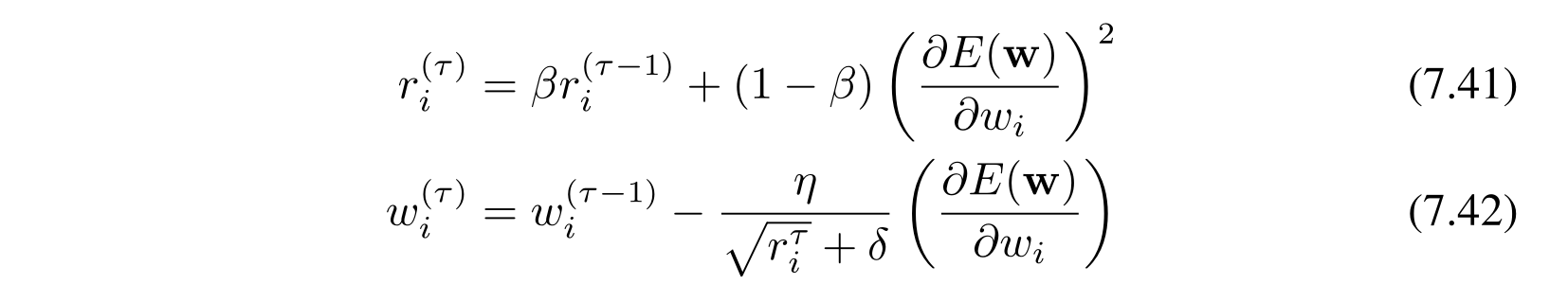
将 RMSporp 和 momentum 结合起来就是现在非常常见的 Adam 方法：

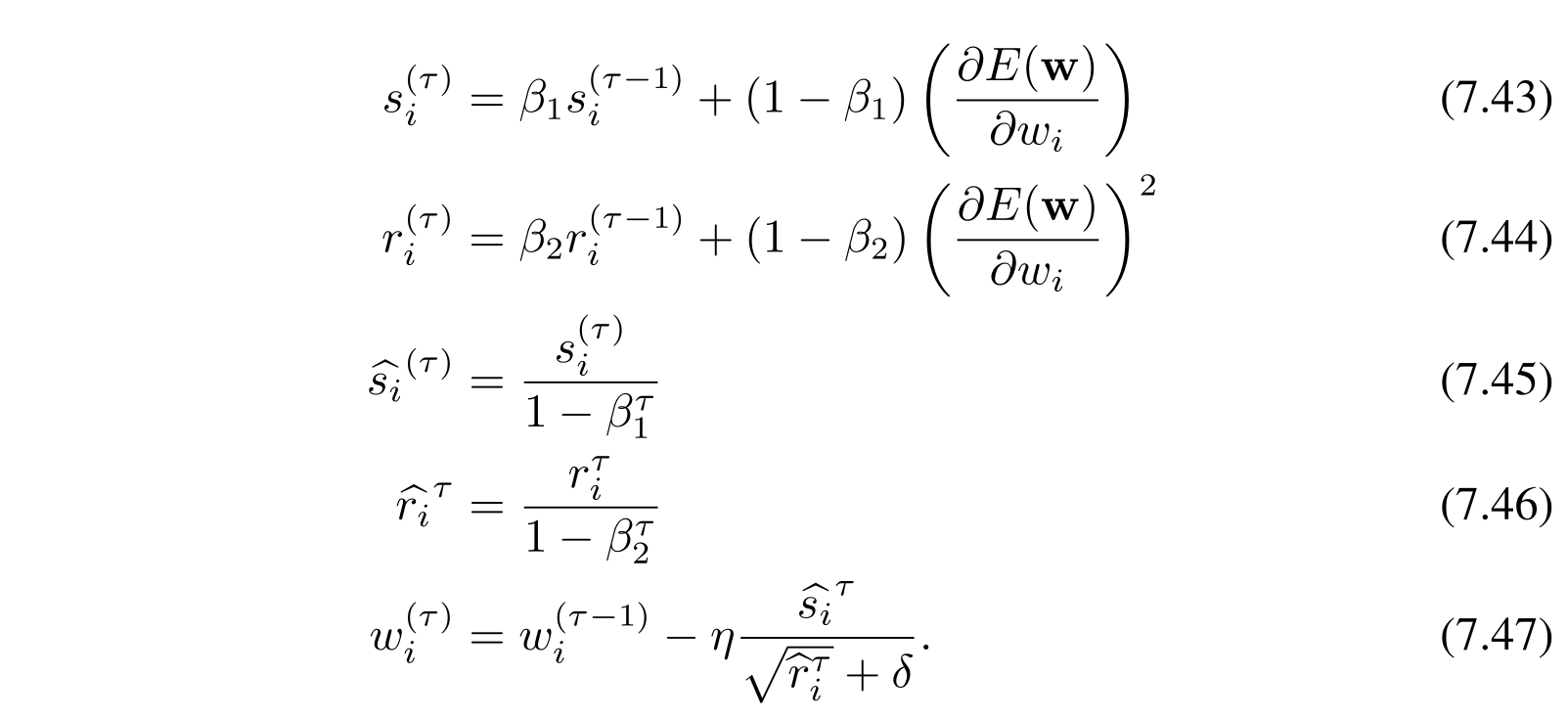
这张图里的 \(\beta_1\) 和 \(\beta_2\) 的设置，原论文也进行了一些实验

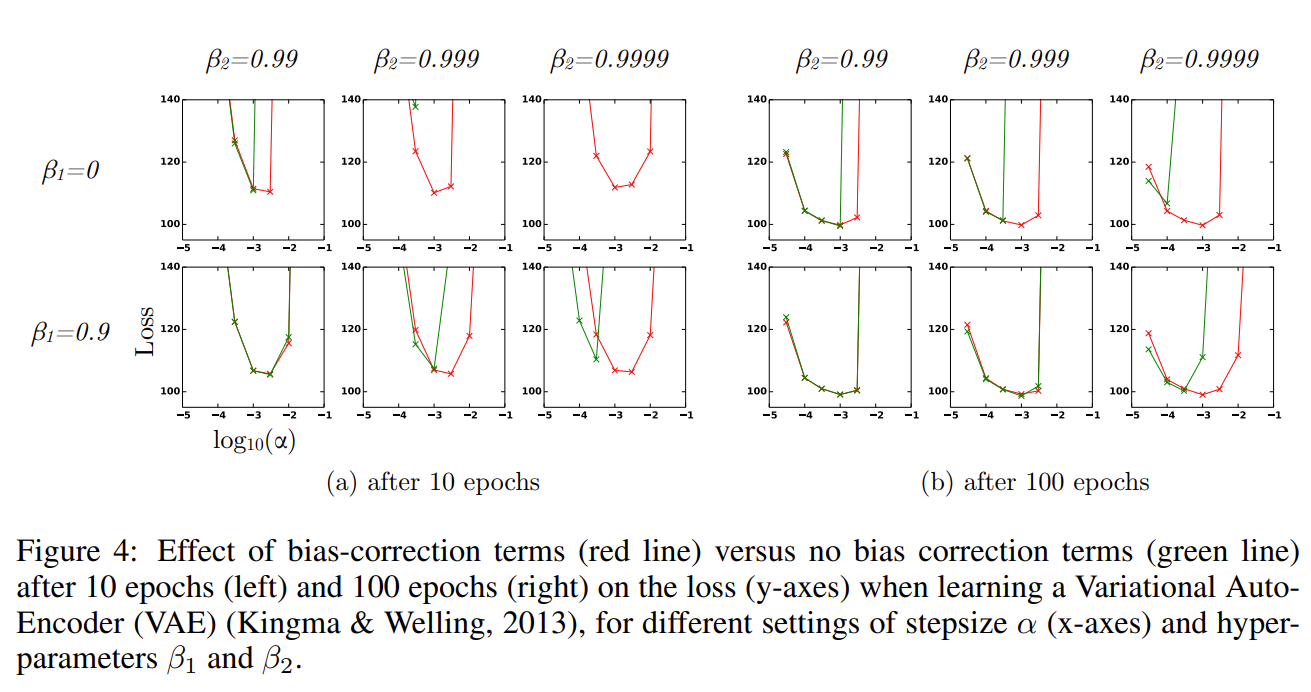
看起来很有道理，但是它真的好吗？

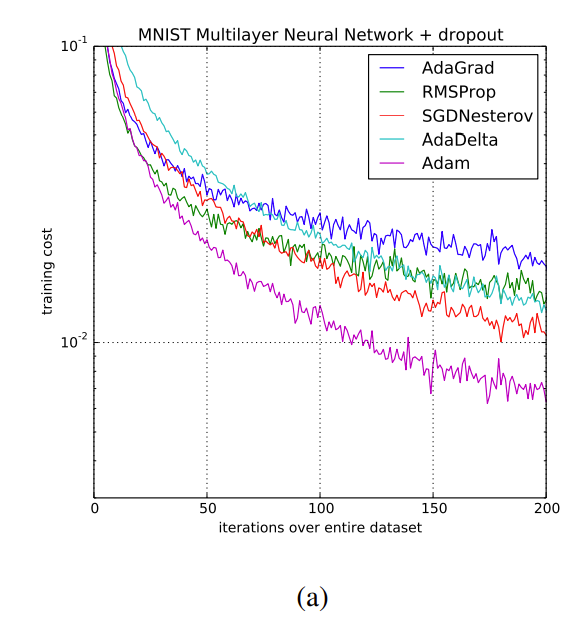
上面这张图来自 adam 原论文。

【总结前面】

反向传播

【前置知识】

有向无环图

---

考虑每个可以学习的参数 \(w_i\)，假设 loss function 是 \(f\)，现在即求 \(\dfrac{\partial f}{\partial w_i}\)

考虑一个简单的网络结构 \(f(X) =\sigma_n\left( W_n(\sigma_{n-1}(W_{n-1}(\dots W_1(X))))\right)\)设 $y_i = W_i(\sigma_{i-1}(W_{i-1}\dots W_1(X)),z_i =\sigma_i(y_i) $ ，这时候\(f(X) = L(z_n,Y)\) ，其中 \(Y\) 表示 \(X\) 这条数据的标签。

此时可学习的参数就是 \(W_1\dots W_n\) 这些矩阵中的元素。容易知道 \(\dfrac{\partial f}{\partial z_{n,i}}\)，将这些元素堆叠成一个 \(n\times 1\) 的向量就是 \(\dfrac{\partial f}{\partial z_n}\) 进而通过链式法则可以知道 \(\dfrac{\partial f}{\partial y_n}\)。

考虑利用 \(\dfrac{\partial f}{\partial y_n}\) 计算 \(\dfrac{\partial f}{\partial W_{n,i,j}}\) 和 \(\dfrac{\partial f}{\partial z_{n-1}}\) 对于每个 \(W_{n,i,j}\) 这个偏导数是不难表达出来的，然后我们可以整合起来表达成简洁的向量乘矩阵的形式。

在具体实现的时候，我们建立神经元之间的有向图，我们可以通过正向传播网络的结构来确定反向传播的过程。

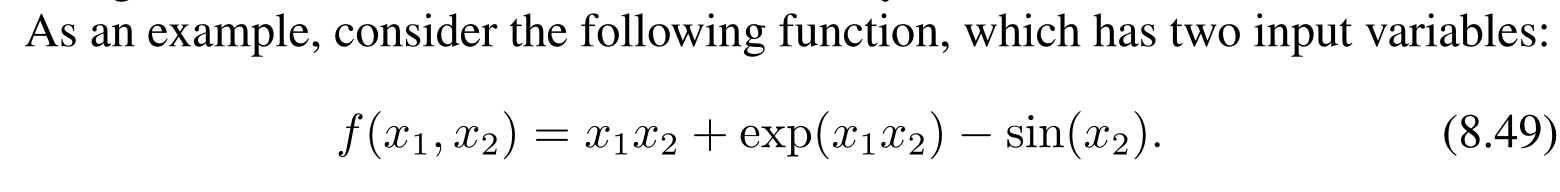
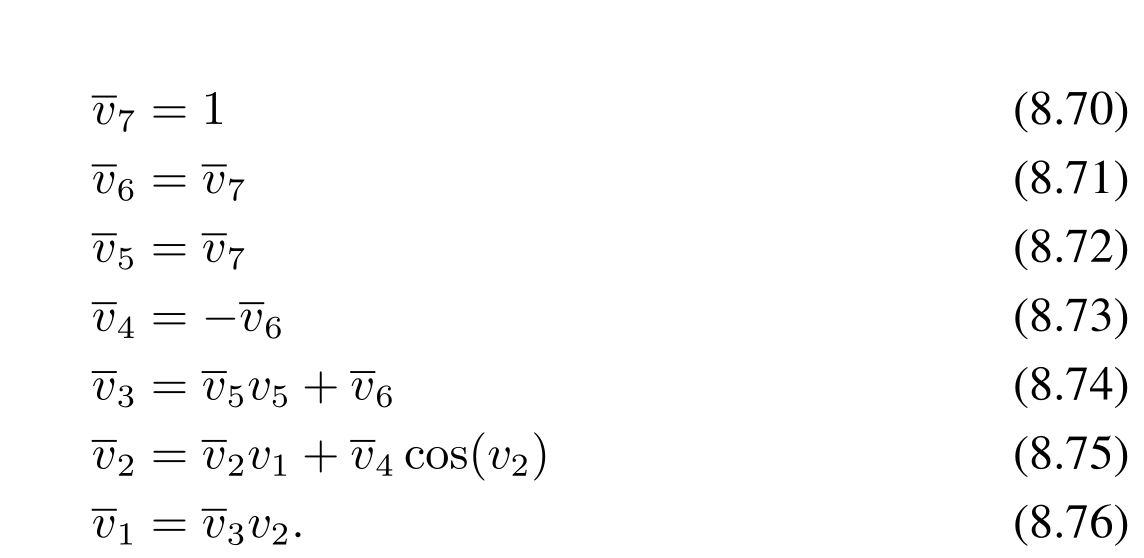
我们通过建立有向图将手写梯度计算表达式变成了存储中间变量和带权的边（边权是类似于 \(y=kx\) ,\(y=\cos x\) 的表达式）。

其实有一个可能的疑问是边数是和 加减乘除/初等函数 数量相同的，会不会因为建立了有向图关系导致边数远远大于点数？答案是不会。原因也显然。

【总结前面】

参数初始化的策略

直觉方法：所有可学习的参数全是初始化成 0。得到了一个死人。

不这样做的原因其实是，一个大网络中间有10层 Wx,f(Wx) 就是对结果重新赋权值。反向传播时这几层梯度也都一样。所以是废的。

用别的网络的参数来初始化当前网络。非常有启发性的做法：
应用：finetune LLM/meta learning

normalization

假设现在要对 \({x_1,\dots x_n}\) 做 normalization

先计算 \(\mu = \cfrac 1n \sum\limits_{i=1}^n x_i,\sigma^2 = \cfrac1n\sum_{i=1}^n (x_i-\mu) ^2\)，然后令 \(x_i' =\dfrac{x_i-\mu}{\sigma}\)。

效果：\(x_i\) 变成了平均值为 \(0\)，方差为 \(1\) 的数列。

考虑到 \(\sigma\) 可能为 0 ，所以 \(x_i' = \dfrac{x_i-\mu}{\sqrt {\sigma^2 + \epsilon}}\) ，这里的 \(\epsilon\) 和上面说的 \(\delta\) 类似。但其实 \(\sigma = 0\) 的话，\(x'_ i \equiv 0,\forall i\in [1,N]\)

data norm

对所有的 data 做 normalization。motivation 就是为了减少噪声对训练的影响。

【为什么噪声会对网络训练造成影响】

batch norm

你现在有一个 batch 的 \(x_i\)，\(n\) 为 batch size，令 \(\mu =\frac 1n\sum\limits_{i=1}^n x_i,\sigma^2=\frac 1n\sum\limits_{i=1}^n (x_i-\mu)^2,\hat x_i=\frac{x_i-\mu}{\sqrt{\sigma^2+\epsilon}},y_i=\beta \hat x_i+\gamma\)。batch normalization 得到的结果就是 \(y_i\)。

\(\epsilon\) 是一个极小的常数，为了避免除 0（类似二分的 eps），

\(\beta,\gamma\) 不是超参数，也不是 \(\beta_i,\gamma_i\)。

• why batch normalization?

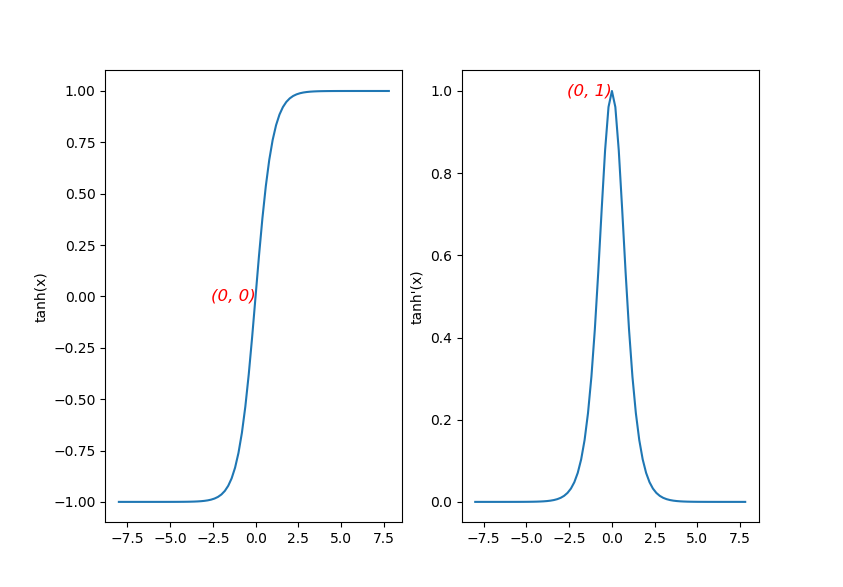
  大概是我们希望使用一些非线性的激活函数对数据进行拟合。比如使用 \(\tanh\)。但是在 back propagation 的过程中如果大量数据落到趋近于 \(\infty\) 的地方，导数是非常小的。通过观察函数图像可以知道，\(\tanh\) 在 \(0\) 附近导数线性。那么我们需要一种方法使得数据集中到 \(0\) 的较小的一个邻域。于是使用 batch normalization。

  \(\tanh\) 及其导数的图像。

• why \(y_i=\beta \hat x_i+\gamma\)?

  据说是一种对数据过于集中的 trade off，防止激活函数变成 y=x。但是这样的描述太过于哲学了。

• How to normalize queries?

  对所有查询进行 normalization 即可。

【总结前面】

drop out