蓝桥杯 最大公共子串（第八届第六题）

标题：最大公共子串
最大公共子串长度问题就是： 求两个串的所有子串中能够匹配上的最大长度是多少。
比如：“abcdkkk” 和 “baabcdadabc”， 可以找到的最长的公共子串是"abcd",所以最大公共子串长度为4。
下面的程序是采用矩阵法进行求解的，这对串的规模不大的情况还是比较有效的解法。

请分析该解法的思路，并补全划线部分缺失的代码。

#include <stdio.h>
#include <string.h>

#define N 256
int f(const char* s1, const char* s2)
{
	int a[N][N];
	int len1 = strlen(s1);
	int len2 = strlen(s2);
	int i,j;
	
	memset(a,0,sizeof(int)*N*N);
	int max = 0;
	for(i=1; i<=len1; i++){
		for(j=1; j<=len2; j++){
			if(s1[i-1]==s2[j-1]) {
				a[i][j] = __________________________;  //填空
				if(a[i][j] > max) max = a[i][j];
			}
		}
	}
	
	return max;
}

int main()
{
	printf("%d\n", f("abcdkkk", "baabcdadabc"));
	return 0;
}

注意：只提交缺少的代码，不要提交已有的代码和符号。也不要提交说明性文字。

结果：a[i-1][j-1]+1
分析：a[i][j]表示两个字符串的第i位和第j位上连续匹配的字符个数，如果i和j不匹配，a[i][j]为0，匹配则在a[i-1][j-1]的基础上加1。把两个字符串分别以行列组成一个二维矩阵，比如str=acbcbcef，str2=abcbced，我们可以得到下面的矩阵，比较二维矩阵每个点对应行列是否相等，相等设为1否则为0，查找出值为1的最长对角线长度就能得到最长公共子串。

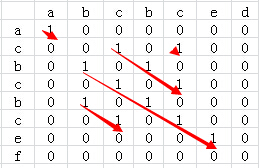
为了进一步优化算法的效率，我们可以再计算某个二维矩阵的值的时候顺便计算出来当前最长的公共子串的长度，即某个二维矩阵元素的值由a[i][j]=1演变为a[i][j]=a[i-1][j-1]+1，这样就避免了后续查找对角线长度的操作了。修改后的二维矩阵如下

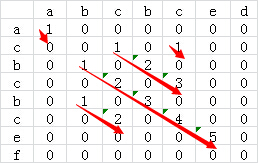
参考：
https://blog.csdn.net/u010397369/article/details/38979077