快速排序（填坑法的两种写法以及交换法）

快速排序

快速排序有多种分割方法。

填坑法

start指针指向开始，end指针指向结束。以a[start]为基准，目的是把数组从基准分开，左边都是小于等于基准的，右边都是大于基准的。先把基准保存，从左右指针互相填坑，遇到不符合规矩的数交换，所以start左边都是小于基准的，end右边都是大于基准的，这样一步一步缩小[start,end]范围，基准肯定位于start,end中间，最后start==end,将基准放这儿。
举个例子，[5,4,6,7,8,9],基准为5,左右指针开始分别位于5,9，右指针先走，寻找第一个小于5的数，找到了4，于是填坑[4,4,6,7,8,9]，注意开始已经将5保存了，5的位置是一个坑，现在start=5，end=4，start继续走寻找大于5的，到了4，不能大于end所以结束了，start，end都在4（索引为1），把基准放进去。结束。

#include <iostream>
using namespace std;

void qs(int a[], int start, int end){
    if(start>=end)return;

    int l=start,r=end;
    int p = a[l];
    while(l < r){
        while(a[r] >= p && l < r) r--;
        a[l] = a[r];
        while(a[l] <= p && l < r) l++;
        a[r] = a[l];
    }
    a[l] = p;
    qs(a,start,l-1);
    qs(a,l+1,end);
}

int main(){
//    freopen("input.txt","r",stdin);
    int t[]={4,2,2,6,9,9,1,3};
    int len= sizeof(t)/ sizeof(int); 
    qs(t,0,len-1);
    for (int i = 0; i < len; ++i) {
        cout<<t[i];
    }
}

加一个包装函数，就是这样的

#include <iostream>
using namespace std;

int partition(int a[], int start, int end){

    int p = a[start];
    while(start < end){//判断条件也可以为start!=end,因为最终start==end
        while(a[end] >= p && start < end) end--;//从右向左第一个小于p的,这里>=不能改为>,否则会不能处理重复元素情况
        a[start] = a[end];
        while(a[start] <= p && start < end) start++;//从左向右第一个大于p的
        a[end] = a[start];
    }
    a[start] = p;
    return start;
}

void qs(int a[], int start, int end){
    if(start<end){
        int mid = partition(a, start, end);
        qs(a, start, mid-1);
        qs(a, mid+1, end);
    }

}

int main(){
//    freopen("input.txt","r",stdin);
    int t[]={4,2,2,6,9,9,1,3};
    int len= sizeof(t)/ sizeof(int);
    qs(t,0,len-1);
    for (int i = 0; i < len; ++i) {
        cout<<t[i];
    }
}

这个循环还有另一种形式

    while(l < r){
        while(a[r] > p && l < r) r--;
        if(l<r)a[l++] = a[r];
        while(a[l] < p && l < r) l++;
        if(l<r)a[r--] = a[l];
    }

填坑了需要前进一步，上面那种形式不需要前进是因为自循环里面的判断条件是a[r]>=p或a[l]<=p，下一次循环会接着往前走，有一种常见的错误是写成这样的。

错误示范

    while(l < r){
       while(a[r] > p && l < r) r--;
       a[l] = a[r];
       while(a[l] < p && l < r) l++;
       a[r] = a[l];
   }

这种形式的分割，遇到重复元素会出错，比如排序[1,1]，基准元素是1，j寻找小于等于基准元素，发现不用动，本来的位置就满足，然后i向后移动，寻找大于等于基准的元素，发现也不用动，本来的位置就满足，陷入了死循环。

填坑法两种分割函数

一：

    while(l < r){
        while(a[r] >= p && l < r) r--;
        a[l] = a[r];
        while(a[l] <= p && l < r) l++;
        a[r] = a[l];
    }

二：

    while(l < r){
        while(a[r] > p && l < r) r--;
        if(l<r)a[l++] = a[r];
        while(a[l] < p && l < r) l++;
        if(l<r)a[r--] = a[l];
    }

交换法

交换法和填坑法原理差不多，注意最后有一个和基准元素交换的过程，

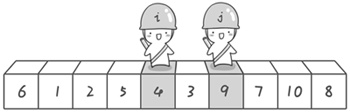
假设我们i，j元素分别到了4和9，j继续向左移动，发现了3（比基准元素6小）停下来，i也继续向右移动，i和j相遇了，结束。此时i和j相遇的位置一定比基准元素小，为什么呢，我们分析一下，相遇有两种情况，1是j移动过程发现了比基准小的元素停下来，然后i继续前进遇到了j，这种情况，j的位置肯定比基准元素小，最后的位置的左右边分别是小于基准和大于基准的，把基准元素放这肯定也没问题；2是j移动过程中没有遇到比基准小的元素，而是直接遇到了i，以前面为例子，如果中间不是3而是12，

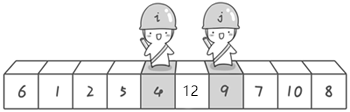
那么j向左移动与i相遇于4这里，i肯定也是小于基准的。所以我们最后需要将基准位置和ij相遇位置的元素互换。

注意：这里每层的两个while循环判断必须用<=

#include <iostream>
using namespace std;

void qs(int *a,int start,int end){
    if(start>=end)return;
    int l=start,r=end;
    int p=a[l];
    while (l!=r){
        while (a[r]>=p&&l<r)r--;//找到小于基准的元素
        while (a[l]<=p&&l<r)l++;//找到大于基准的元素
        if(l<r) {//最后如果是l==r就没必要交换
            swap(a[l], a[r]);
        }
    }
    swap(a[l],a[start]);
    qs(a,start,l-1);
    qs(a,l+1,end);
}
int main(){
//    freopen("input.txt","r",stdin);
    int t[]={4,2,2,6,9,9,1,3};
    int len= sizeof(t)/ sizeof(int);
    qs(t,0,len-1);
    for (int i = 0; i < len; ++i) {
        cout<<t[i];
    }
}

参考：
填坑法参考： https://blog.csdn.net/a4118000113209/article/details/51923095
交换法参考：http://wiki.jikexueyuan.com/project/easy-learn-algorithm/fast-sort.html