蓝桥杯 方格填数（第七届第六题）dfs 全排列

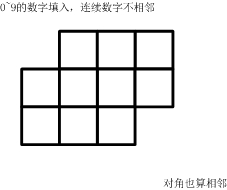
方格填数

如下的10个格子

填入0~9的数字。要求：连续的两个数字不能相邻。
（左右、上下、对角都算相邻）

一共有多少种可能的填数方案？

请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

解法一：

枚举全排列，全排列的结果保存在nums数组里面，nums数组按照顺序放的是3x4个格子的数（第一个格子和最后一个格子没数我们用-1代替，这样的目的是为了一维能向二维转化），我们需要判断这中放置方法是否合理，对于nums中的每一个数，分解出它在二维坐标中的位置，对于相邻的八个方向如果有值和当前位置的值相等则说明这个放置方法不合理。如果所有位置都没有发现有相邻的，则当前放置方法合理，可能的方案数加1。

#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>

using namespace std;

vector<int> nums={-1,0,1,2,3,4,5,6,7,8,9,-1};

bool test(){
    for(int i=1;i<nums.size()-1;i++){
        int r=i/4;
        int c=i%4;
        for(int dx=-1;dx<=1;dx++)
            for(int dy=-1;dy<=1;dy++){
                if(dx!=0||dy!=0){//遍历8个方向
                    int nr=r+dx;
                    int nc=c+dy;
                    if(nr<0||nr>=3||nc<0||nc>=4)continue;//遇到出界的忽略
                    if((nr==0&&nc==0)||(nr==2&&nc==3))continue;//遇到左上和右下的忽略
                    if(abs(nums[nr*4+nc]-nums[i])==1)return false;//判断是否相邻
                }
            }
    }
    return true;
}

int main(){
    int cnt=0;
    do{
//        for(int t:nums)cout<<t<<" ";
//        cout<<endl;
        if(test())cnt++;
    }
    while (next_permutation(nums.begin()+1,nums.end()-1));

    cout<<cnt;

}

上面那种方法可以优化一下，将遍历八个方向改为按顺序只遍历四个方向

#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>

using namespace std;

vector<int> nums={-1,0,1,2,3,4,5,6,7,8,9,-1};
int dir[4][2]={{-1,-1},{0,-1},{-1,0},{-1,1}};

bool test(){
    for(int i=1;i<nums.size()-1;i++){
        int r=i/4;
        int c=i%4;
        for(int k=0;k<4;k++){
            int nr=r+dir[k][0];
            int nc=c+dir[k][1];
            if(nr<0||nc<0||nr>=3||nc>=4)continue;
            if(nr==0&&nc==0)continue;
            if(abs(nums[nr*4+nc]-nums[i])==1)return false;
        }
    }
    return true;
}

int main(){
    int cnt=0;
    do{
//        for(int t:nums)cout<<t<<" ";
//        cout<<endl;
        if(test())cnt++;
    }
    while (next_permutation(nums.begin()+1,nums.end()-1));

    cout<<cnt;

}

解法二：

从左到右，从上到下填数，将当前位置能填的数全部尝试一遍，然后去填下个位置的数，如果能到达最后位置，解法加1。由于是按照从左到右从上到下的顺序填数的，所以只用判断上面3个位置和左边一个位置（已经填过的）和当前的数是否相邻。当前位置的数还没有填所以我们将当前要填的数传入判断函数中。

 

#include <bits/stdc++.h>

using namespace std;

int cnt;
int vis[10];
int g[3][4];
int dir[4][2]={{0,-1},{-1,-1},{-1,0},{-1,1}};


bool judge(int r,int c,int v){
//我们将数组初始化为一个极大值，虽然这里的[0,0]位置没有排除掉，但是没有关系，它永远也不会和任何数相邻
    for(int i=0;i<4;i++){
        int nr=r+dir[i][0];
        int nc=c+dir[i][1];
        if(nr>=0&&nr<3&&nc>=0&&nc<4){
            if(abs(g[nr][nc]-v)==1)return false;
        }
    }
    return true;
}

void dfs(int r,int c){
    if(r==2&&c==3){
        cnt++;
        return;
    }

    for(int i=0;i<=9;i++){
        if(!vis[i]&&judge(r,c,i)){
            vis[i]=1;
            g[r][c]=i;
            c!=3?dfs(r,c+1):dfs(r+1,0);
            vis[i]=0;
        }
    }
}

int main(){
    for(int i=0;i<3;i++)for(int j=0;j<4;j++)g[i][j]=INT_MAX;
    dfs(0,1);
    cout<<cnt;
}