海明码浅析

海明码

首先，海明码是一种基于偶校验的一种校验码，只适用于编码有一位出错的情况。

海明码的位数

对于原来的n位信息码\(D_4D_3D_2D_1\)，我们为其加上k位校验码，也就是一共n + k位

对于这n + k位码，每一位都有可能出错，因此对于每一种出错情况加起来一共n + k种状态，再加上全部正确的情况，因此一共n + k + 1中状态。

而k位校验码，因为是二进制，所以一共能表示\(2^k\)种状态。

因此，我们校验码能表示的状态要大于等于可能出现的状态，即\(2^k\ge n + k + 1\)

另外第i位校验码\(P_i\)要放在海明码的第\(2^{i - 1}\)位上

海明码个人理解

我们假设信息位为 1010，此时n = 4，可得k = 3

我们先确定校验位的分布：

\(H_7\)	\(H_6\)	\(H_5\)	\(H_4\)	\(H_3\)	\(H_2\)	\(H_1\)
\(D_4\)	\(D_3\)	\(D_2\)	\(P_3\)	\(D_1\)	\(P_2\)	\(P_1\)
1	0	1	？	0	？	？

我们对于这7位海明码的信息位序号先进行二进制转换，即

\(H_3:3 \rightarrow 0 1 1\)

\(H_5:5 \rightarrow 1 0 1\)

\(H_6:6 \rightarrow 1 1 0\)

\(H_7:7 \rightarrow 1 1 1\)

而第 i 位校验码可以理解为掌管着信息码序号的第 (i - 1) 位二进制位上为 1 的那些信息码（这样有助于最后统一确认错误代码的位置，后面会解释）

那么第 1 位校验码也就掌管着 \(H_3、H_5、H_7\)，因为他们的第 0 位二进制位上为 1

同理可得，

第 2 位校验码掌管着 \(H_3、H_6、H_7\)

第 3 位校验码掌管着 \(H_5、H_6、H_7\)

那么，我们该如何确定每一位校验码\(P_i\)上是 0 还是 1 呢？

最开始提过，海明码是一种基于偶校验的一种校验码，因此对于每一位校验码加上其掌管的那些信息位一共有偶数个 1 即可

举一个例子：

对于第一位校验码和其掌管的信息位 \(P_1、H_3、H_5、H_7\)，我们只需要让这四个数字有偶数个 1 即可，因为 信息位为 1010，所以此时不算 \(P_1\) 已经有 2 个 1 了，因此我们得到 \(P_1\) 为 0，我们可以用异或的方式来计算 \(P_1\)，即

\(P_1 = H_3\bigoplus H_5 \bigoplus H_7\)

依次计算，我们最后就可以得到我们所要的海明码了。

那么对于已知的一串海明码我们又该如何确定错误的那一位呢？

理解了上面的，这个就非常简单了，还是以第一位校验码举例子，我们只需要计算 \(P_1 \bigoplus H_3\bigoplus H_5 \bigoplus H_7\)的值是否为 0，如果为 0 则说明校验码\(P_1\)和其掌管的信息位没有错，如果为 1 则说明错误的位置序号的二进制下第 0 位 有 1 的那些序号

那么最终就可以得到一个数字，这里借用王道视频的一张图

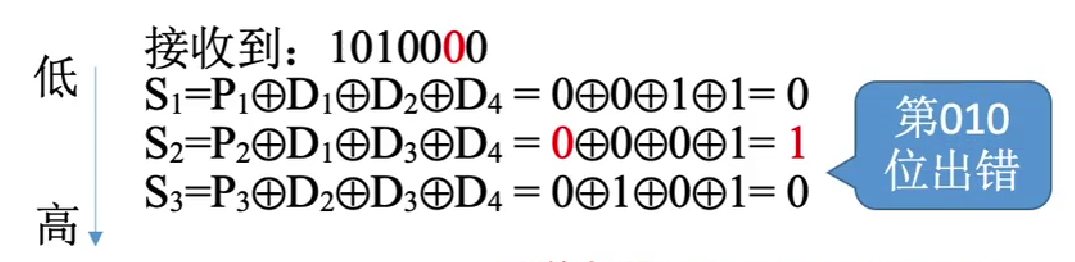
也就是第 2 个数字错了

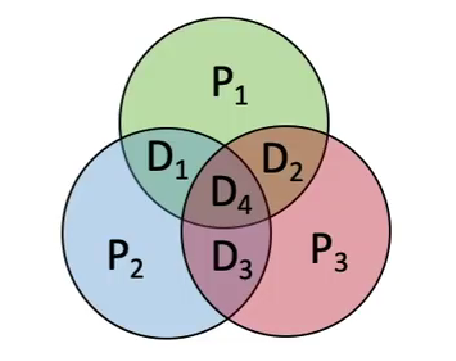
在这里我们要体会一下上面的那个“有”字，我们可以用一张集合的图来表示