神经网路

此系列笔记来源于

Coursera上吴恩达老师的机器学习课程

---

用神经网络表示逻辑回归问题

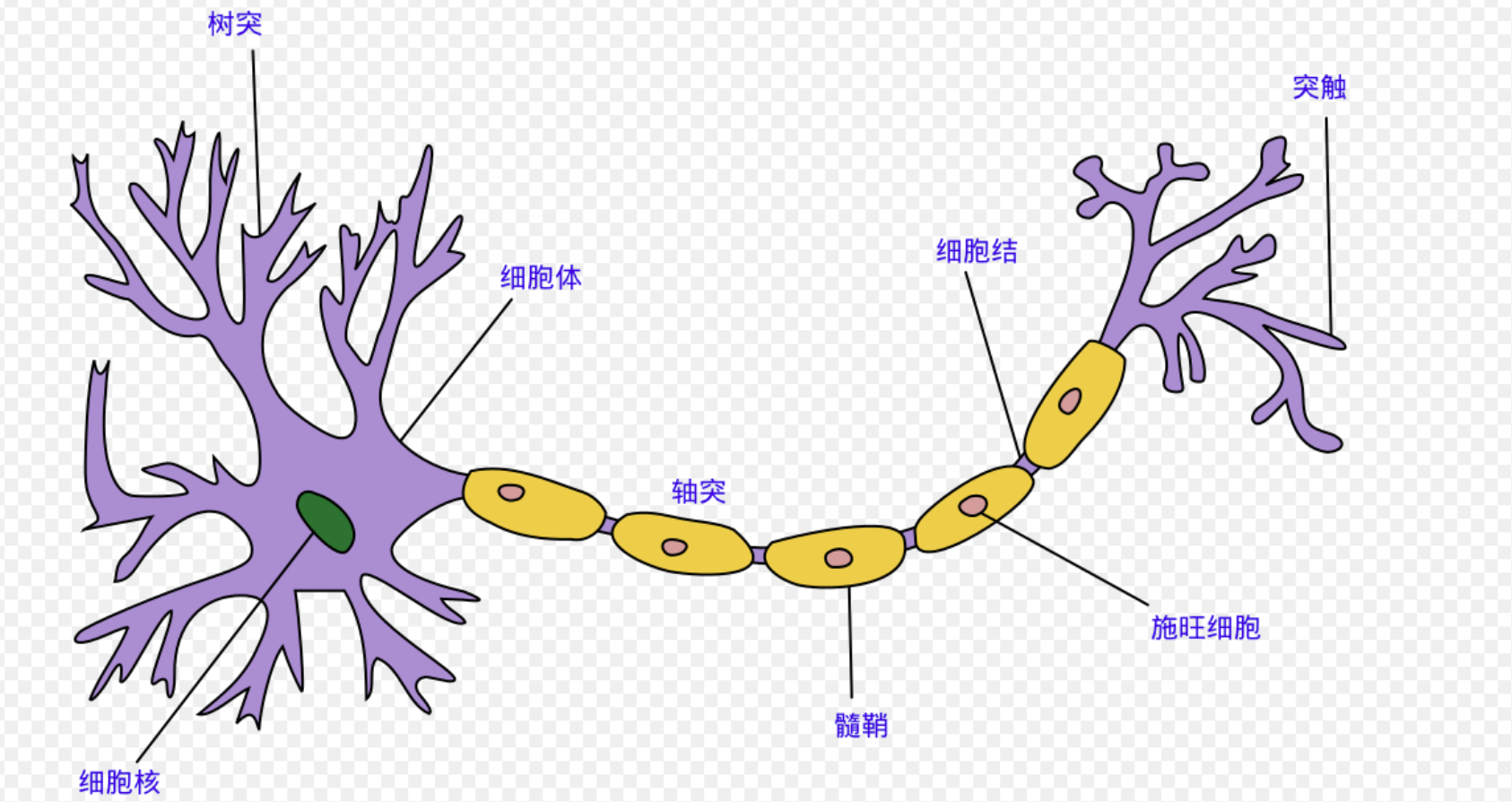
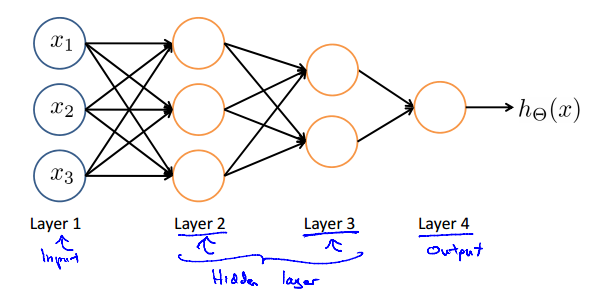
我们的输入作为树突进行电输入，并被传输到轴突作为输出。

这里的输出就是各个特征\(x_1 \cdots x_n\)，输出便是我们的假设函数，另外在这个模型中，我们称输入\(x_0\)为偏置单元（类似于线性方程 \(y = kx + b\) 中的截距 \(b\)），其总等于1

同时，我们称逻辑函数 \(g = \frac{1}{1+e^{-\theta^Tx}}\) 为（逻辑）激励函数(sigmoid activation function)，而参数 \(\theta\) 被称为权重

模型可以简单被表示为：

\([x_0\;x_1\;x_2] \rightarrow [\;\;] \rightarrow h_\theta(x)\)

而第一层特征的输入被称为 输入层，最后一层假设函数的输出被称为 输出层

而在输入层和输出层中间的被称为隐藏层，中间的\(a_0^2\cdots a_n^2\)被称为激活单元

模型便可以表示为：

\([x_0\;x_1\;x_2\;x_3] \rightarrow [a_1^{(2)}\;a_2^{(2)}\;a_3^{(2)}] \rightarrow h_\theta(x)\)

此处的激活单元可以被表示成

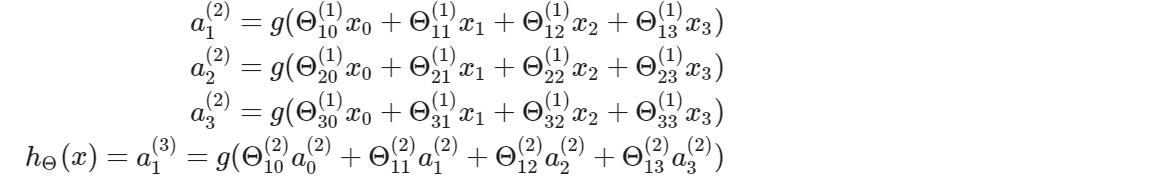
计算这些激活单元是通过一个存放参数的矩阵 \(\Theta^{(j)}\)

如果第 \(j\) 层中有 \(s_j\) 个单元，第 \(j + 1\) 层中有 \(s_{j + 1}\) 个单元，那么 \(\Theta^{(j)}\) 的纬度便是 \(s_{j+1} \times (s_j + 1)\)，这里的 \(+1\) 来自偏置单元····

我们令\(a_i^{(2)} = g(z_i^{(2)}),\;i=1、2、3\)，即\(z_k^{(2)} = \Theta_{k,0}^{(1)}x_0+\Theta_{k,1}^{(1)}x_1+\cdots+\Theta_{k,n}^{(1)}x_n\)

向量化后的\(x\)和\(z^j\)为 \(x=\begin{bmatrix}x_0\\x_1\\\cdots\\x_n\end{bmatrix},\;z^{(j)}=\begin{bmatrix}z_1^{(j)}\\z_2^{(j)}\\\cdots\\z_n^{(j)}\end{bmatrix}\)

我们再令\(x=a^1\)，则\(z^{(j)}=\Theta^{(j-1)}a^{(j-1)},\;a^{(j)}=g(z^{(j)})\)

对于每一层\(j\)，我们还得添加一项\(a_0^{(j)}恒等于1\)

最后一个\(\Theta\)矩阵只有一行，因此最后得到的是一个数字，也就是最终的\(h_\Theta(x)\)

样例 OR function

多类别分类问题

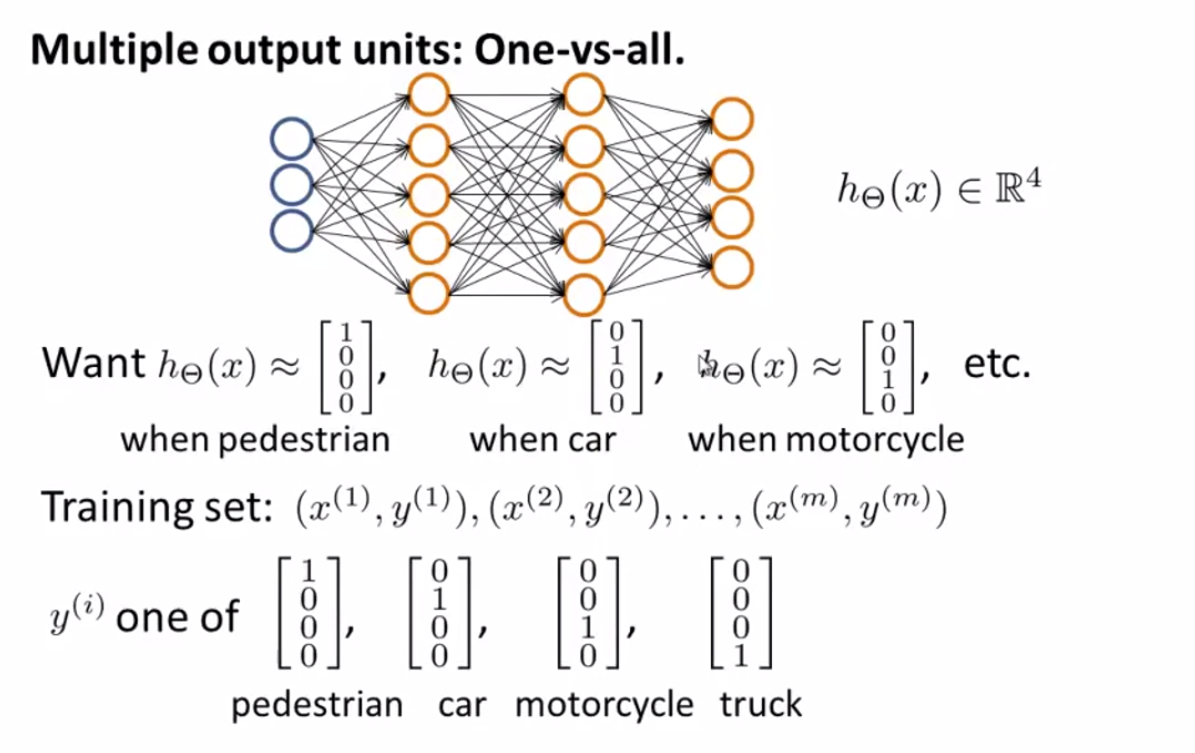
如图，我们根据每个训练集\((x^{(i)},\;y^{(i)})\)，能最终得到一个\(h_{\Theta}(x)\)，如图所示，以此来判断每个训练集属于哪个类别

个人总结

简单来说，神经网络就是一个由输入值、中间隐藏层、输出层构成的学习模型、方法。在每两层之间，我们会设定权重和一个计算方式，权重用\(\Theta\)矩阵表示，第 i 行 第 j 列表示从前一列的第 j 个元素到下一列的第 i 个元素的权重。通过神经网络的层层计算，我们最终便能得到所要的结果。

代价函数

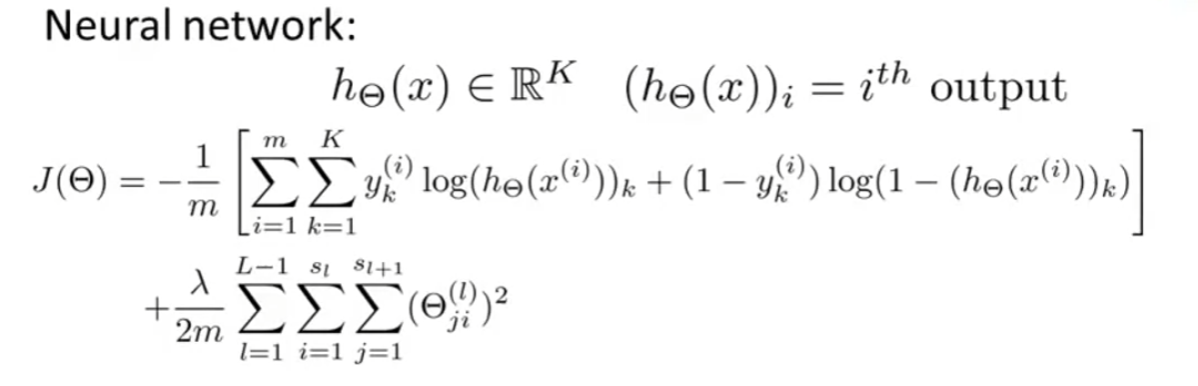
y 是 向量的形式，如 \(\begin{bmatrix} 0 \\ 0 \\ 1 \\ 0\end{bmatrix}\)

反向传播算法 Backpropagation Algorithm

"反向传播 "是神经网络术语，用于最小化我们的成本函数，就像我们在逻辑回归和线性回归中的梯度下降一样。我们的目标是计算\(\min_\Theta J(\Theta)\)，也就是说，我们希望使用\(\Theta\)中的一组最佳参数来最小化我们的成本函数\(J\)。

下面是计算\(J(\Theta)\)偏导的方法

偏导方程：\(\dfrac{\partial}{\partial \Theta_{i,j}^{(l)}}J(\Theta)\)

首先已知训练集

令\(\Delta_{i,j}^{(l)}:=0,\;for\;all\;(l,i,j)\)

接下来对于每一组训练样本 \(t=1,2,3,\cdots,m\)

1、令\(a^{(1)}:=x^{(t)}\)

并且通过前向传播(forward propagation) 计算\(a^{(l)},\;l=1,2,3,\cdots,L\)

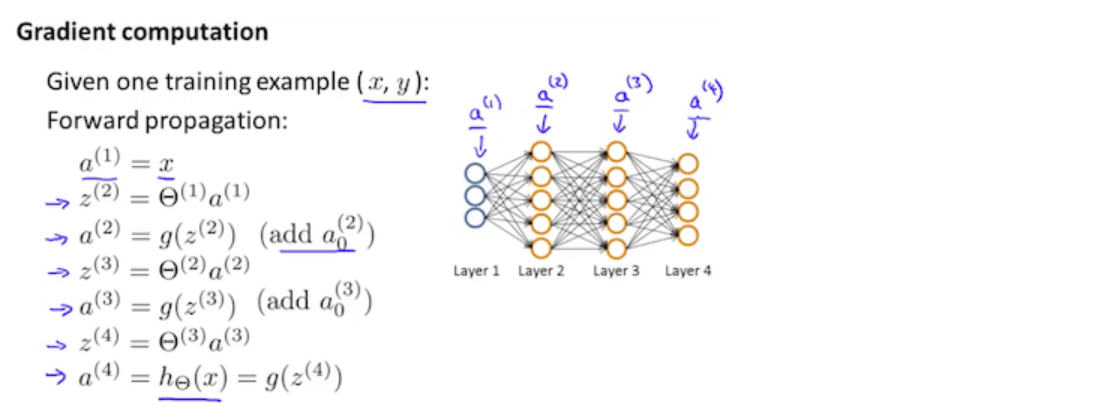
3、先根据\(y^{(t)}\)，计算 \(\delta^{(L)}=a^{(L)}-y^{(t)}\)，其中 L 是总层数，\(a^{(L)}\)是最后一层激活单元的输出向量，因此这里的误差值计算就是最后一层的实际结果和y中的正确输出之间的差值

4、进行反向传播

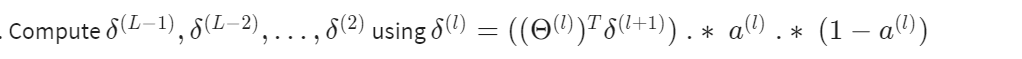
这里的 \(a^{(l)}\;.*\;(1-a^{(l)})\) 是 g函数的导数，即 \(g'(z^{(l)})=a^{(l)}\;.*\;(1-a^{(l)})\)

另外注意 \(\delta\) 到第二层计算就结束了，第一层没有，并且每一层的各个 \(\delta\) 只与当前层和下一层有关。

5、计算\(\Delta\)

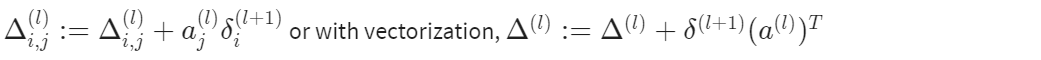
右边的是向量化后的公式。

最后我们便能得到

而\(\frac{\part}{\part\Theta_{i,j}^{(l)}}J(\Theta)=D_{i,j}^{(l)}\)

另外，在单分类和单组数据的情况下，我们可以这样来理解

系数矩阵展开至向量

为了能使用优化函数，如“fminunc()”，我们需要将 \(\Theta\) 和 \(D\) 矩阵放进一个长向量里面

thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ]
deltaVector = [ D1(:); D2(:); D3(:) ]

如此一来我们便可以将矩阵传参给优化函数

然后我们需要获取各个系数矩阵 假设 Theta1 和 Theta2 都是10x11 的矩阵，Theta3 是 1x11 的矩阵

获取方式如下：

Theta1 = reshape(thetaVector(1:110),10,11) %把长向量第 1-110 个元素放进一个 10 x 11 的矩阵
Theta2 = reshape(thetaVector(111:220),10,11)
Theta3 = reshape(thetaVector(221:231),1,11)

总结：

梯度检验

反向传播算法以及一些其他算法非常复杂，因此十分容易出现bug，哪怕答案貌似正确，因此我们需要使用梯度检验，来保证正确性。

梯度检验简单来说就是通过数值计算来验证梯度计算的正确性，公式：

对于单个 \(\Theta\)：

对于多个 \(Theta\)：

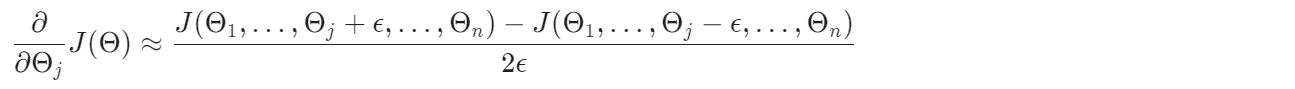
另外，\(\epsilon\)不宜太小，避免出现数值计算的错误，一般来说 \(1e^{-4}\) 较为合适

代码：

epsilon = 1e-4;
for i = 1 : n,
  thetaPlus = theta;
  thetaPlus(i) += epsilon;
  thetaMinus = theta;
  thetaMinus(i) -= epsilon;
  gradApprox(i) = (J(thetaPlus) - J(thetaMinus)) / (2 * epsilon)
end;

并且，我们一旦验证了一次反向转播算法是正确的后，就不要再次计算 gradApprox，因为用数值计算来验证梯度的方法，代码运行效率非常低。

随机初始化

随机初始化的目的是打破对称性，对称性指 当初始化权重矩阵时，填充了相等的值，那么神经元在向前向后传播时的表现相似。

因此我们会对权重矩阵随机初始化

%If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.
Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON; %[-epsilon, epsilon]
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;

总结

训练一个神经网络的步骤：

1、随机初始化权重矩阵

2、对各个训练集，用前向传播计算 \(h_\Theta(x^{(i)})\)

3、使用 cost function 计算代价

4、使用反向传播算法计算偏导 \(\frac{\part}{\part\Theta_{i,j}^{(l)}}J(\Theta)\)

5、用梯度检验 来确保反向传播算法正确运行，检验完便不再梯度检验

6、利用梯度下降算法或者内置优化算法 和 反向传播算法 来更改权重矩阵，以此最小化代价函数

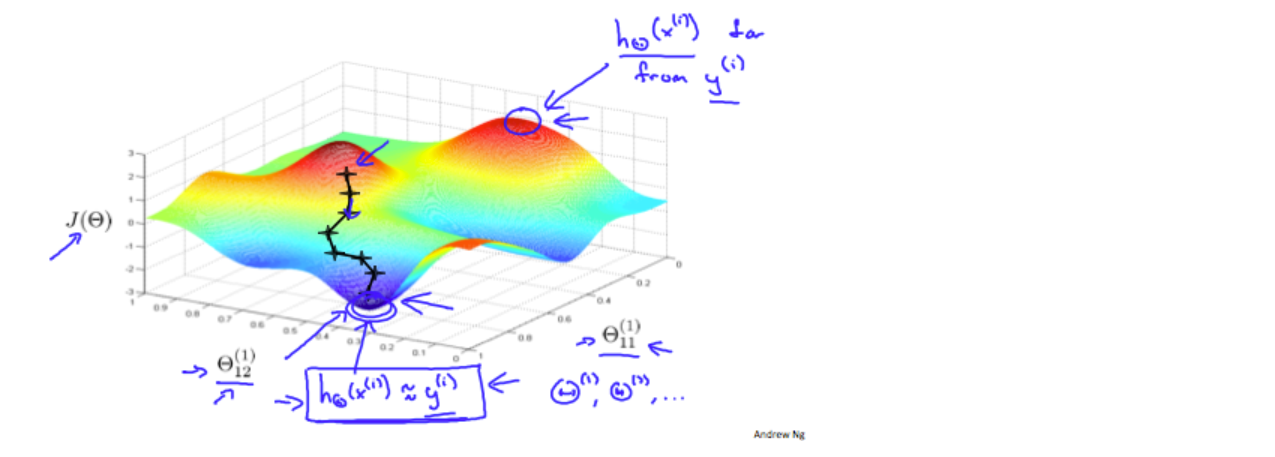
在最小化过程中，反向传播算法用来确认下降方向。