逻辑回归问题

此系列笔记来源于

Coursera上吴恩达老师的机器学习课程

---

逻辑回归问题

逻辑回归问题由于历史原因，是属于分类问题的一种

下面都以二元分类问题为例

假设函数

在线性回归问题中，我们设定假设函数为\(h_\theta(x) = \theta^Tx\)

但在逻辑回归问 题中，如果\(y\in\{0,\;1\}\)，那么显然\(h_\theta<0\;or\;h_\theta>1\)是不合理的。为了能有利于分类，我们便希望\(0 \le h_\theta(x) \le 1\)。

因此我们设\(h_\theta=g(\theta^Tx),\;g(z) = \frac{1}{1 + e^{-z}},\;z=\theta^Tx\)

我们称\(g(z)\)为逻辑函数 Logistic Function 或者 Sigmoid Function

函数图像如下：

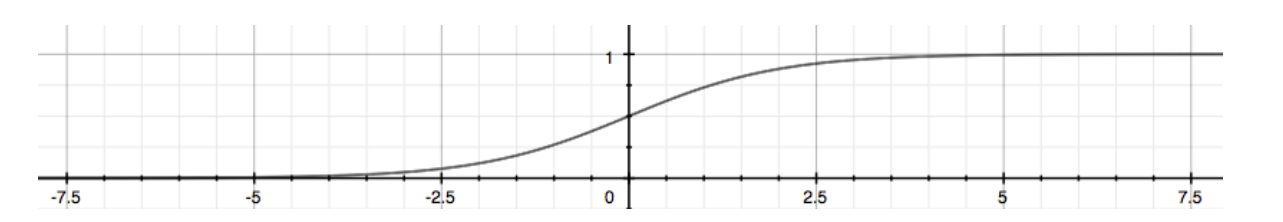
这样对任意\(x\in\R\)我们都可以得到\(h_\theta(x)\in(0,\;1)\)

而在这里的\(h_\theta(x)\)告诉了我们输出值为1的可能性，同时输出值为0的可能性也就是\(1 - h_\theta(x)\)

\(h_\theta(x) = P(y=1|x;\theta)=1-P(y=0|x;\theta)\)

决策边界

当 \(h_\theta < 0.5\) 时，我们预测 0，当 \(h_\theta \ge 0.5\) 时，我们预测 1。

我们很容易发现当 \(z \lt 0\) 时，我们会得到 0，而 \(z \ge 0\) 时，我们会得到 1

根据训练集，我们拟合出 \(\theta\) 后便能得到 \(z(x)\) 的表达式。从而我们便能根据 \(z(x) \ge 0\;或者\;z(x) < 0\) 来画出图像，从而得到这一条决策边界，帮助我们划分出两块区域。

例：

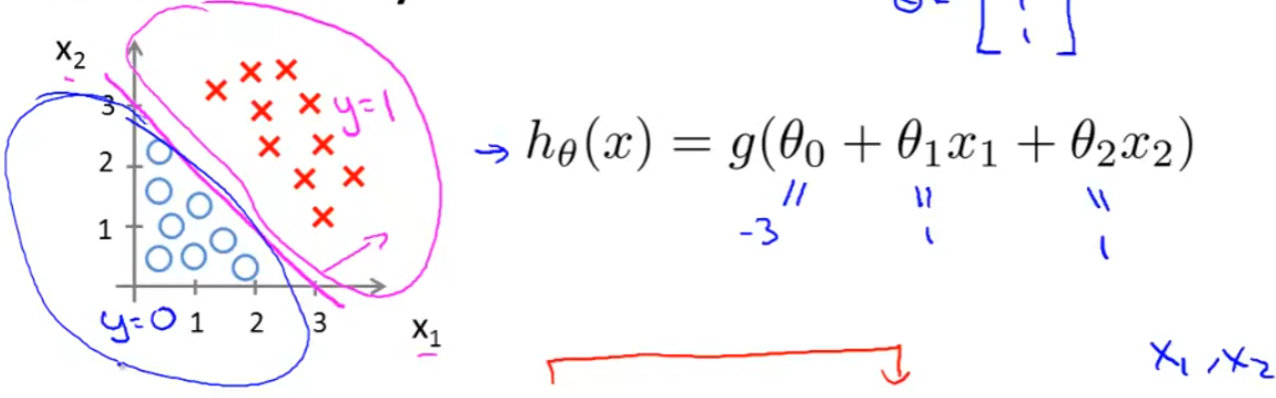
代价函数

为了能使用梯度下降算法，我们希望代价函数是凸函数(convex)，因此我们令

\(J(\theta)=\frac{1}{m}\sum^m_{i=1}Cost(h_\theta(x^{(i)},\;y^{(i)}))\)

\(Cost(h_\theta(x),\;y)=-log(h\theta(x))\;\;\;if\;y = 1\)

\(Cost(h_\theta(x),\;y)=-log(1-h\theta(x))\;\;\;if\;y = 0\)

函数图像如下：

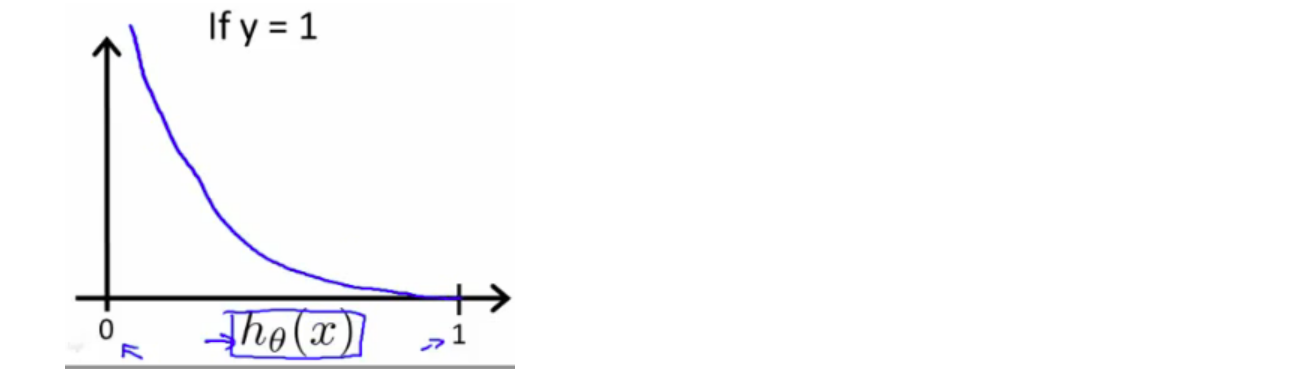
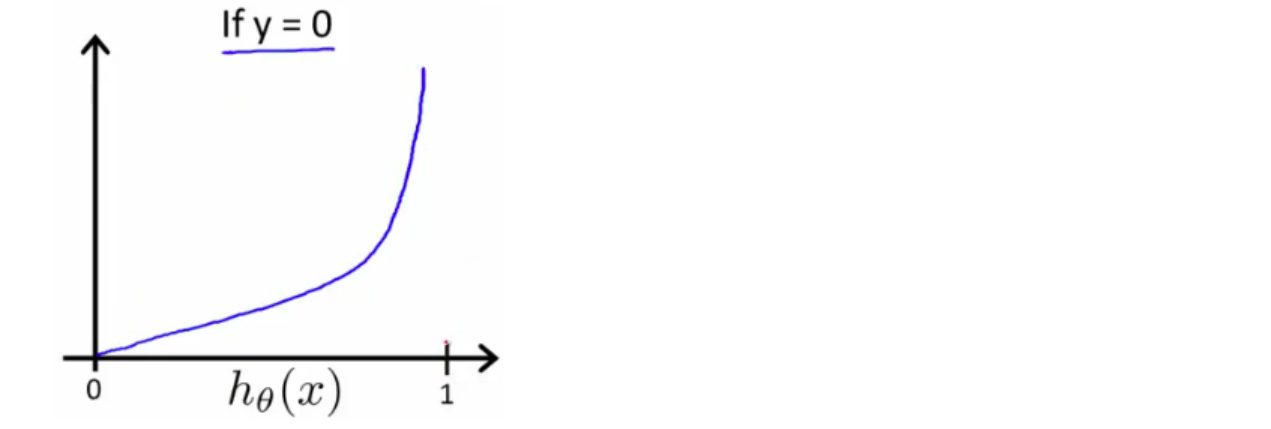
我们可以知道当 \(h_\theta=y\) 时，\(Cost(h_\theta,\;y) = 0\)

而当 \(h_\theta\rightarrow t\;且\;t\neq y\) 时，则 \(Cost(h_\theta,\;y)\rightarrow\infin\)

可以理解为学习了一个错误，花了极大代价。

如此一来，我们便能令代价函数为凸函数，为了逻辑回归。

最终我们还可以简化 Cost函数，不用分类，即：

\(Cost(h_\theta(x),\;y)=-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))\)

代价函数则为：

\(J(\theta)=-\frac{1}{m}\sum^m_{i=1}[y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)}))]\)

向量化(vectorized) 后则为：

\(h=g(X\theta)\)

\(J(\theta)=\frac{1}{m}\cdot(-y^Tlog(h)-(1-y)^Tlog(1-h))\)

梯度下降算法

运用到梯度算法中，公式并没有改变，区别仅在于 \(h_\theta\) 函数的改变。

\(Repeat \{\)

\(\theta_j:=\theta_j-\frac{\alpha}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}\)

\(\}\)

向量化后：

\(Repeat \{\)

\(\theta:=\theta-\frac{\alpha}{m}X^T(g(X\theta)-\overrightarrow y\;)\)

\(\}\)

Advanced Optimization

"Conjugate gradient", "BFGS", and "L-BFGS"比起梯度下降更加高效，但更加复杂。我们可以通过调用相关被封装好的库函数，来代替梯度下降。

首先我们需要写一个函数，根据 \(\theta\) 得到 \(J_\theta\) 和 \(\frac{\part}{\part\theta_j}J(\theta)\)

f unction [jVal, gradient] = costFunction(theta)
  jVal = [...code to compute J(theta)...];
  gradient = [...code to compute derivative of J(theta)...];
end

之后便可以通过调用 “fminunc()”函数 和 “optimset()”函数来进行计算

options = optimset('GradObj', 'on', 'MaxIter', 100); %GradObj 'on'意味着要给该算法提供一个梯度，MaxIter 100意味着最多迭代一百次
initialTheta = zeros(2,1);
   [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

多元分类

当 y 的值拓宽到 1 - n 时，我们可以将问题转化为二元分类问题

我们设定 n 个分类器，每个分类器将第 i 个类和其他类分为两类。

即：\(h_\theta^{i}(x) = P(y=i|x;\theta),\;i\in\{0,1...n\}\)

此时我们的 prediction值即为\(max_i(h_\theta^{(i)}(x))\)

过度拟合 Overfitting

过度拟合指的是，根据训练集，我们设定的假设函数过度与训练集拟合，这可能会对接下来的预测产生不好的影响。

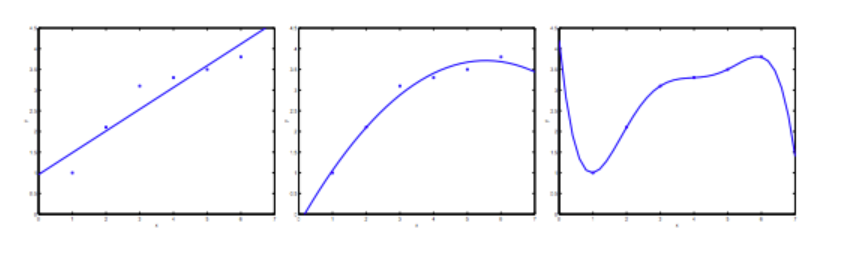
在线性回归问题中，当我们设定的特征函数不够拟合训练集，称为 ”欠拟合“(underfitting) 或者 “高偏差“(high bias)，相反过度拟合训练集时，称为”过度拟合“(overfitting) 或者 “高方差”(high variance)

而这两种情况都无法很好的预测数据的趋势。

如何解决这两种情况：

1、减少特征数量

2、正则化 Regularization

正则化 Regularization

为了去减少特征值的影响力，而不是直接删除，我们可以通过加一些项来达到这一效果。

这样一来，如果原来假设函数是一个四次函数，且我们通过正则化去减少最高两项的系数\(\theta_3\) 和 \(\theta_4\)的值，从而使假设函数更加quadratic，那么便能得到一个更为简单的假设，更不易发生过度拟合。

同理，我们可以通过一个式子对所有 \(\theta\)参数进行正则化：

$ min_\theta\frac{1}{2m}[\sum^{m_{i=1}(h_\theta(x})-y^{(i)})2+\lambda\sum^{n_{j=1}\theta_j}2]$

\(\lambda\) 称为正则化参数。正则化参数过大可能会导致欠拟合，

正则化后的线性回归

梯度下降：

\(Repeat \{\)

\(\theta_0:=\theta_0-\frac{\alpha}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)}\)

\(\theta_j:=\theta_j-\alpha[(\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)})+\frac{\lambda}{m}\theta_j],\;j\in\{1,2 ...n\}\)

\(\}\)

在这里，\(\frac{\lambda}{m}\theta_j\)便是正则化的部分。

第二个式子进行变形后可以得到：\(\theta_j:=\theta_j(1-\alpha\frac{\lambda}{m})-\frac{\alpha}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}\)

而第一项中的 \(1-\alpha\frac{\lambda}{m}\) 始终小于1

正规方程

经过证明后，我们可以得到 \(X^TX+\lambda\cdot L\) 是一定可逆的

正则化后的逻辑回归

代价函数

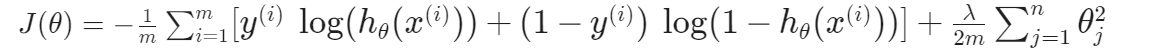
梯度计算

\(\frac{\part J}{\theta_j}=\frac{1}{m}\sum^m_{i=1}((h_\theta(x^{(i)})-y^{(i)})x_j^{(i)})+\frac{\lambda}{m}\theta_j,\;for\;j\ge1\)

梯度下降

\(Repeat \{\)

\(\theta_0:=\theta_0-\frac{\alpha}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)}\)

\(\theta_j:=\theta_j-\alpha[(\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)})+\frac{\lambda}{m}\theta_j],\;j\in\{1,2 ...n\}\)

\(\}\)