线性回归问题

此系列笔记来源于

Coursera上吴恩达老师的机器学习课程

---

线性回归问题

回归问题中，根据已给的数据集，需要拟合出一个线性的函数，用以预测数据。

代价函数

均方误差函数 Mean squared error

$J(\theta_0, \theta_1) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{ (i)})^2$

前面有个二分之一是为了计算机更好的计算梯度下降，因为求导后$\frac12$会被指数2消掉

我们假设拟合曲线为$h_\theta(x) = \theta_1x$，那么对于不同的$\theta1$我们都可以计算出其对应的$J(\theta1)$的值，那么便可以对$J(\theta)$作出相关函数，便可以求得我们所要的最优解。

梯度下降算法

可以用来最小化代价函数 J

假设代价函数 $J(\theta_0,\theta_1)$，并设置一个初始点

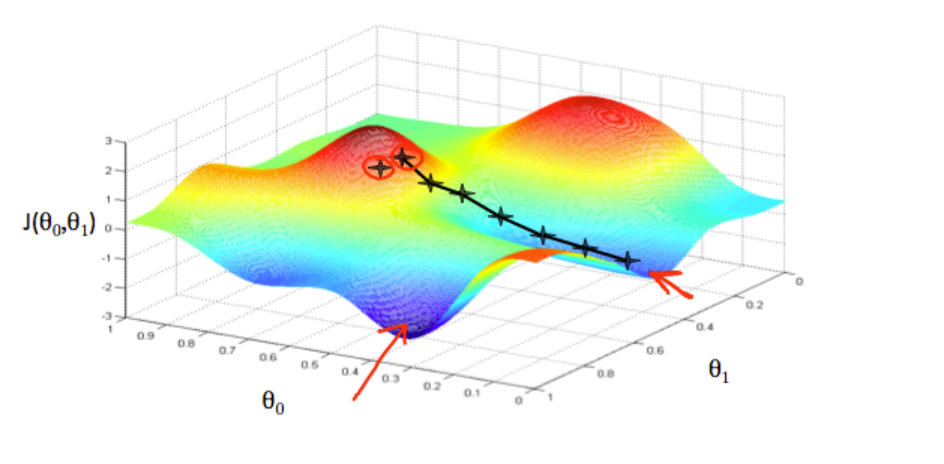
我们从初始点开始，不断进行计算：

$\theta_j:=\theta_j-\alpha\frac{\part}{\part\theta_j}J(\theta_0, \theta_1)，j =0、1$

即$\theta_j:=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)},\;(j=0,1)$

最终也就到达了我们所要的代价函数最小值点

PS：

1、:=为赋值运算符，将右边的值赋给左边

2、在这里$\theta_0$和$\theta_1$为同步更新，即

$①temp0:=\theta_0-\alpha\frac{\part}{\part\theta_0}J(\theta_0, \theta_1)$

$②temp1:=\theta_1-\alpha\frac{\part}{\part\theta_1}J(\theta_0, \theta_1)$

$③\theta_0:=temp0$

$④\theta_1:=temp1$

②式和3式不能颠倒，这将导致我们在计算②式的偏导时会产生错误，从而得出错误的答案

3、$\alpha$是学习速率，它决定了我们在图中的每一步的size，而偏导$\frac{\part}{\part\theta_1}J(\theta_0, \theta_1)$则决定了我们的移动方向，另外每一步的起点不同，那么最后所到达的终点也可能会不同。

4、在计算中我们不需要去减小$\alpha$的值，因为随着梯度下降，我们的导数也会趋于零（当导数为0时，即得到了optimal minimum），随之我们的每次下降的步伐也将越来越小。

5、另外$\alpha$如果太小那么最终求解时间会过长，$\alpha$太大那么最终可能会使得函数值为无法converge，甚至diverge

多元线性回归

当线性回归函数涉及到多个变量时，便是多元线性回归

假设函数 $h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3+...+\theta_nx_n$

将 $\theta$ 和 $x$ 作为向量分别用矩阵表示，同时$x^{(i)}_{j}$表示第 i 组样例的第 j 个特征

$\begin{bmatrix}\theta_0 & \theta_1 &... & \theta_n \end{bmatrix}$ 和 $\begin{bmatrix} x_0 & x_1 & ... & x_n \end{bmatrix},\;此处假设\;x_0 = 1$

就可以更精炼的得到：

$h_\theta(x)=\begin{bmatrix}\theta_0 & \theta_1 &... & \theta_n \end{bmatrix}\begin{bmatrix} x_0 \\ x_1 \\ ... \\ x_n \end{bmatrix}=\theta^Tx$

而此时梯度下降算法中，也从$n = 1$变为 $n \ge 1$：

$\theta_j:=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)},\;(j=0,1...,n)$

特征放缩 和 均值归一

当特征值 $\theta$ 在很大的变量范围上、变量值不均匀时，会下降的很慢。

比如对于两个特征值，再画出轮廓图后可能是一个非常细长的椭圆。

而我们可以改变每个输入变量$x_{(i)}$的范围，使得它们大致相同来缓解这一情况。

在这里我们将用到 特征放缩(Feature Scaling) 和 均值归一(Mean Normalization) 两个方法

特征放缩指 将输入值 除以 范围值(即最大值减最小值) 或者 标准差，均值归一指 将输入值 减去 平均值。

表示为：$x_i=\frac{x_i-\mu_i}{s_i},\;s_i表示范围值或标准差,\;\mu_i表示平均值$

关于学习速率 $\alpha$

对于学习速率 $\alpha$ 我们知道，如果选择的过大，可能会导致随着每次迭代，代价函数不断增加，如果选择的过小，可能会导致求最优解的迭代时间过长。

同时，我们还可以写一个自动收敛检测，当一次迭代的值 E 小于某个很小的值比如 $10^{-3}$时，就停止迭代。然而一般这个阈值的确定十分困难。

关于特征值

有时候我们可以组合已知的特征，来得到新的特征，这样有时可能会令假设函数更优。

例如：我们可以组合$x_1,\;x_2$进行相乘，来得到一个新的特征$x_3$，这样可以将两个特征合并成一个特征

多项式回归

对于一个假设函数 $h_\theta(x)=\theta_0+\theta_1x_1$

如果该线性的假设函数并不适用于我们的问题，那么我们可以通过创造新的特征值来改变该函数使得其更符合实际问题，比如创造$x_2 = x_1\cdot x_1 \cdot, \;x_3=x_1\cdot x_1\cdot x_1$

即 $h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3$

但要注意的是，此时$x_2\;和\;x_3$的范围分别是$x_1$的次方和立方，因此特征放缩便十分重要了。

正规方程 Normal Equation

在最小化代价函数，求解 $\theta$ 时，我们往往会采用梯度下降的算法。但其实当数据量较小时，我们可以采用正规方程的方法求解。

解法如下：

令$\theta=\begin{bmatrix} \theta_0 \\ \theta_1 \\ ... \\ \theta_n \end{bmatrix},\;y=\begin{bmatrix} y_1 \\ y_2 \\ ... \\ y_n \end{bmatrix},\;X=\begin{bmatrix} (x^{(1)})^T \\ (x^{(2)})^T \\ ... \\ (x^{(m)})^T \end{bmatrix},\;(x^{(i)})^T=\begin{bmatrix} x^{(i)}_0 & x^{(i)}_1 & ... & x^{(i)}_n \end{bmatrix}$ ，往往我们令$x^{(i)}_0 = 1$，则

$\theta = (X^TX)^{-1}X^Ty$

正规方程和梯度下降法的比较

梯度下降法：1、需要选择学习速率 2、需要迭代 3、$O(kn^2)$ 4、当 n 较大时运行速率更快

正规方程法：1、不需要选择学习速率 2、不需要迭代 3、$O(n^3)$，受计算逆矩阵影响 4、当 n 较大时运行速率缓慢

当矩阵$X^TX$不可逆时，

这是一种比较少见的情况，我们一会采用删除一些无用的特征值（如两个特征值为线性关系、平方关系…）或者正规化方法。

另外在matlab、octave中，有pinv(A) 和 inv(A)两种方法。对呸于奇异矩阵或者非方阵可以用 pinv(A) 求其伪逆，且不会产生错误。

假设函数的式子（向量化）

$h_\theta(x) = \theta^Tx$