最小生成树MST

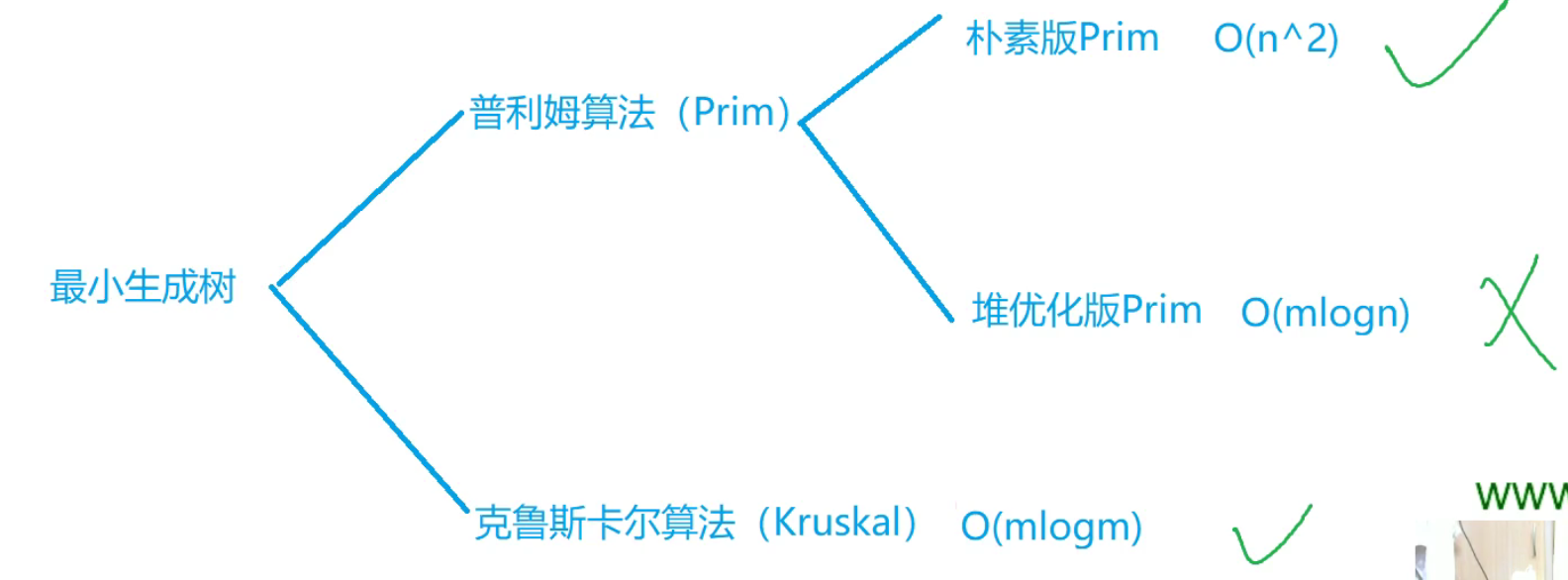
最小生成树(MST)

对于稀疏图：

1、朴素Prim算法 时间复杂度\(O(n^2)\)

算法分析：和朴素Dijkstra的算法流程十分相似，定义集合S表示最小生成树的集合，每次先找出集合外距离集合最近的点t，随后再用t去更新其他点到集合的距离。

858. Prim算法求最小生成树 - AcWing题库

代码示例:

//#pragma comment(linker,   "/STACK:10240000000000,10240000000000")
//#pragma GCC optimize(2)

#include <bits/stdc++.h>
using namespace std;

#define For(i,a,b) for (int i=(a);i<=(b);++i)
#define Fod(i,b,a) for (int i=(b);i>=(a);--i)
#define mls multiset
#define lb lower_bound
#define ub upper_bound
#define pb push_back
#define pob pop_back
#define itt iterator
#define endl '\n'
#define IOS ios::sync_with_stdio(0); cin.tie(0);
#define lowbit(x) x & (-x)
#define clr(x) memset(x, 0, sizeof(x));
#define fi first
#define se second

typedef vector<int> vii;
typedef vector<long long> vll;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
		
const int MAXN = 0x3f3f3f3f;
const int MOD = 1000000007;
const ll MOD1 = 212370440130137957ll;

const int N = 505;
const int M = 1e5 + 5;

int g[N][N];
int n, m;
int dist[N];
bool st[N];

int prim()
{
	memset(dist, 0x3f, sizeof dist);
	int res = 0;
	for(int i = 0; i < n; i ++)
	{
		int t = -1;
		for(int j = 1; j <= n; j ++)
			if(!st[j] && (t == -1 || dist[j] < dist[t])) t = j;
		if(i && dist[t] == MAXN) return MAXN;
		if(i) res += dist[t]; 
		st[t] = true;
		for(int j = 1; j <= n; j ++) //保存完dist[t]的值之后再去更新，以防出现自环的情况
			dist[j] = min(dist[j], g[t][j]);
	}
	return res;
}

int main ()
{	
	//IOS;
	cin >> n >> m;
	memset(g, 0x3f, sizeof g);
	for(int i = 1; i <= m; i ++)
	{
		int a, b, c;
		cin >> a >> b >> c;
		g[a][b] = g[b][a] = min(g[a][b], c);
	}

	int t = prim();
	if(t == MAXN) puts("impossible");
	else cout << t << endl;

	return 0;
}	
/*

*/	

对于稠密图：

1、Kruskal算法 时间复杂度\(O(mlogm)\)

算法分析：先将每个点看作一棵独立分离的树，之后先将所有边按边权从小到大进行排序，然后遍历每条边进行两点的相连，若两点连通则相连，否则不连，判断方式可以用并查集。最终当连的边数为n-1条时，即存在最小生成树（所有点皆连通），过程中再用个res记录下每条连接的边的边权和即可

859. Kruskal算法求最小生成树 - AcWing题库

代码示例：

//#pragma comment(linker,   "/STACK:10240000000000,10240000000000")
//#pragma GCC optimize(2)

#include <bits/stdc++.h>
using namespace std;

#define For(i,a,b) for (int i=(a);i<=(b);++i)
#define Fod(i,b,a) for (int i=(b);i>=(a);--i)
#define mls multiset
#define lb lower_bound
#define ub upper_bound
#define pb push_back
#define pob pop_back
#define itt iterator
#define endl '\n'
#define IOS ios::sync_with_stdio(0); cin.tie(0);
#define lowbit(x) x & (-x)
#define clr(x) memset(x, 0, sizeof(x));
#define fi first
#define se second

typedef vector<int> vii;
typedef vector<long long> vll;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
		
const int MAXN = 0x7fffffff;
const int MOD = 1000000007;
const ll MOD1 = 212370440130137957ll;

const int M = 2e5 + 5;
const int N = 1e5 + 5;
struct node
{
	int a, b, c;
	bool operator < (const node &x) const
	{
		return c < x.c;
	}
}e[M];
int n, m; 
int p[N];
int res;
int cnt;
int find(int x)
{
	if(x == p[x]) return x;
	return p[x] = find(p[x]);
}

int main ()
{	
	//IOS;
	cin >> n >> m;
	for(int i = 1; i <= m; i ++)
	{
		int a, b, c;
		cin >> a >> b >> c;
		e[i] = {a, b, c};
	}
	sort(e + 1, e + 1 + m);
	for(int i = 1; i <= n; i ++)  p[i] = i;
	for(int i = 1; i <= m; i ++)
	{
		int a = find(e[i].a), b = find(e[i].b);
		if(a != b)
		{
			p[b] = a;
			res += e[i].c;
			cnt ++;
		}
	}
	if(cnt != n - 1) puts("impossible");
	else cout << res << endl;
	return 0;
}	

PS:而对于堆优化版的Prim算法其实和堆优化Dijkstra一样，但算法实现上不如kruskal简单，且时间复杂度差不多，因此不常用。