【uoj428】普通的计数题

Portal --> uoj428

Solution

　　不会胖子的一个log正解qwq只能怂怂滴写分治了qwq

​　　首先就是一个我想不到的转化qwq

​　　我们将第\(i\)次操作加入的数看成一个编号为\(i\)的节点的权值，并且把操作\(2\)中删除的节点看成\(i\)号点的儿子，那么整个操作序列对应一个树结构，并且满足父亲的编号大于儿子，特别的，原来的\(0\)对应了叶子节点，\(1\)对应了非叶子节点，那么原题中的限制就变成了：当某个节点的儿子都是叶子的时候，它的儿子个数在\(B\)集合中，否则叶子儿子的个数在\(A\)集合中

​　　然后为了方便一起处理，我们强行把\(0\)丢到\(B\)集合中，这样叶子节点也满足条件了

​　　于是乎我们就可以dp了：记\(f[i]\)表示\(i\)个节点的满足条件的有根树个数，\(g[i]\)表示\(i\)个节点的满足条件的森林个数，并且森林中每棵树的节点个数不少于\(2\)，那么dp的转移方程为：

\[\begin{aligned} g[i]&=f[i]+\sum\limits_{j=2}^{i-1}g[i-j]\cdot f[j]\binom{i-1}{j-1}\\ f[i]&=[i-1\in B]+\sum\limits_{j=0}^{i-2}[j\in A]\binom{i-1}{j}g[i-1-j] \end{aligned} \]

​　　具体一点的话就是，\(g\)的转移方程中\(j\)枚举的是第\(i\)个点所在树的大小，然后要从前面\(i-1\)个点里面选\(j-1\)个出来和\(i\)号点组成一棵树；\(f\)的转移方程中前半部分是所有的儿子都是叶子的情况，后半部分是枚举叶子儿子的个数，然后\(g[i-1-j]\)表示的是剩下的非叶子儿子有多少种不同的方案

　　接下来正解对这个东西进行一些高级处理然后用牛顿迭代去搞了qwq

​　　然而我并不会所以就用分治

​　　注意到上面的式子其实已经可以直接分治ntt了，把组合数拆一下然后按套路写就好了

　　需要注意的事情是：因为这里计算的\(g\)转移跟自己有关，所以在分治完之后卷积算左边对右边贡献的时候，可能会遇到需要用到的\(g\)还没有算出来（或者是需要用到的\(f\)）的情况，卷积的时候就不会把贡献算进去了，所以这个时候，如果说我们当前的分治区间的左端点不是\(1\)，那么就有可能包含了某个因为还没被算出来而导致贡献漏算的\(g\)或者\(f\)，所以我们应该做两次ntt，把漏算的贡献加回去

​　　其实大概就是这样的情况：

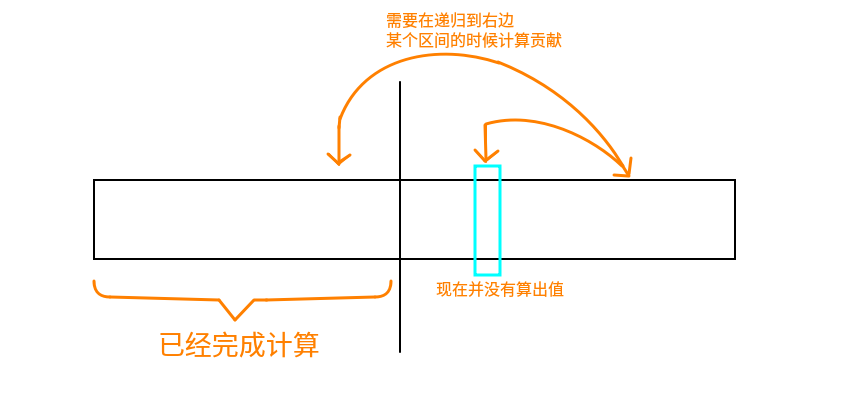
​　　然后实现上就是。。当前分治区间的\(l\neq 1\)时，计算\(g\)的时候，枚举\(g\)的下标在左半边，做一次卷积；再枚举\(f\)的下标在左半边，做一次卷积，顺序的话其实也会有一点影响，\(g\)下标在左半边的那次卷积必须要保证用到的是还没有更新过右半边的\(f\)，否则就会重复计算一些贡献

​　　计算\(f\)的话因为并没有与自己有关，所以直接算就好了不需要考虑那么多

​　　一个小trick：注意到算\(g\)的时候我们的\(j\)是从\(2\)开始枚举的，为了方便我们可以强行先令\(f[1]=0\)然后分治ntt，最后再把\(f[1]\)的值赋回去，这样就中间写的时候就可以比较无脑了

​　　然后就十分愉快地做完了ovo（虽然说是\(O(nlog^2n)\)做法qwq）

Code

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=114514+10,MOD=998244353;
int fac[N],invfac[N];
int inA[N],inB[N];
int f[N],g[N];
int n,m,lena,lenb;
int plu(int x,int y){return (1LL*x+y)-(1LL*x+y>=MOD?MOD:0);}
int mul(int x,int y){return 1LL*x*y%MOD;}
int ksm(int x,int y){
	int ret=1,base=x;
	for (;y;y>>=1,base=mul(base,base))
		if (y&1) ret=mul(ret,base);
	return ret;
}
namespace NTT{/*{{{*/
	const int N=(1<<18)+10,TOP=18,G=3;
	int A[N],B[N],W[N][2],rev[N];
	int len,invlen,invg;
	void prework(){
		invg=ksm(G,MOD-2);
		for (int i=1;i<=TOP;++i){
			W[1<<i][0]=ksm(G,(MOD-1)/(1<<i));
			W[1<<i][1]=ksm(invg,(MOD-1)/(1<<i));
		}
	}
	void get_len(int n){
		for (int i=0;i<len;++i) A[i]=B[i]=0;
		int bit=0;
		for (len=1;len<=n;len<<=1,++bit);
		rev[0]=0;
		for (int i=1;i<len;++i) rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
		invlen=ksm(len,MOD-2);
	}
	void ntt(int *a,int op){
		int w,w_n,u,v;
		for (int i=0;i<len;++i) 
			if (rev[i]>i) swap(a[i],a[rev[i]]);
		for (int step=2;step<=len;step<<=1){
			w_n=W[step][op==-1];
			for (int st=0;st<len;st+=step){
				w=1;
				for (int i=0;i<(step>>1);++i){
					v=mul(a[st+i+(step>>1)],w);
					u=a[st+i];
					a[st+i]=plu(u,v);
					a[st+i+(step>>1)]=plu(u,MOD-v);
					w=mul(w,w_n);
				}
			}
		}
		if (op==1) return;
		for (int i=0;i<len;++i) a[i]=mul(a[i],invlen);
	}
	void calc(){
		ntt(A,1);
		ntt(B,1);
		for (int i=0;i<len;++i) A[i]=mul(A[i],B[i]);
		ntt(A,-1);
	}
}/*}}}*/
void calc(int l,int r){
	int mid=l+r>>1,len=r-l+1,lenl=mid-l+1,lenr=r-mid;
	NTT::get_len(lenl+len);
	for (int i=l;i<=mid;++i) NTT::A[i-l]=mul(g[i],invfac[i]);
	for (int i=0;i<r-l;++i) NTT::B[i]=mul(inA[i],invfac[i]);
	NTT::calc();
	for (int i=mid+1;i<=r;++i) f[i]=plu(f[i],NTT::A[i-l-1]);//f has been updated

	NTT::get_len(lenl+len);
	for (int i=l;i<=mid;++i) NTT::A[i-l]=mul(f[i],invfac[i-1]);
	for (int i=1;i<=r-l;++i) NTT::B[i-1]=mul(g[i],invfac[i]);//should use the one which hasn't been updated
	NTT::calc();
	for (int i=mid+1;i<=r;++i) g[i]=plu(g[i],NTT::A[i-l-1]);

	if (l==1) return;
	NTT::get_len(lenl+len);
	for (int i=l;i<=mid;++i) NTT::A[i-l]=mul(g[i],invfac[i]);
	for (int i=1;i<=r-l;++i) NTT::B[i-1]=mul(f[i],invfac[i-1]);
	NTT::calc();
	for (int i=mid+1;i<=r;++i) g[i]=plu(g[i],NTT::A[i-l-1]);
}
void solve(int l,int r){
	if (l==r){
		if (l>1) //let f[1]=0 first: can't take f[1] into account during the dp
			f[l]=plu(inB[l-1],mul(f[l],fac[l-1]));
		g[l]=plu(f[l],mul(g[l],fac[l-1]));
		return;
	}
	int mid=l+r>>1;
	solve(l,mid);
	calc(l,r);
	solve(mid+1,r);
}
void prework(int n){
	fac[0]=1;
	for (int i=1;i<=n;++i) fac[i]=mul(fac[i-1],i);
	invfac[n]=ksm(fac[n],MOD-2);
	for (int i=n-1;i>=0;--i) invfac[i]=mul(invfac[i+1],i+1);
}

int main(){
#ifndef ONLINE_JUDGE
	freopen("a.in","r",stdin);
#endif
	int x;
	NTT::prework();
	scanf("%d%d%d",&n,&lena,&lenb);
	for (int i=1;i<=lena;++i) scanf("%d",&x),inA[x]=1;
	for (int i=1;i<=lenb;++i) scanf("%d",&x),inB[x]=1;
	inB[0]=1;
	prework(n);
	g[0]=1;
	solve(1,n);
	f[1]=1;
	printf("%d\n",f[n]);

	/*g[0]=1; f[1]=1;
	for (int i=2;i<=n;++i){
		g[i]=0; f[i]=0;
		for (int j=2;j<=i;++j)
			g[i]=plu(g[i],mul(f[j],mul(invfac[j-1],mul(g[i-j],invfac[i-j]))));
		g[i]=mul(g[i],fac[i-1]);
		for (int j=0;j<=i-2;++j)
			f[i]=plu(f[i],mul(inA[j],mul(invfac[j],mul(g[i-1-j],invfac[i-1-j]))));
		f[i]=plu(mul(f[i],fac[i-1]),inB[i-1]);
		g[i]=plu(g[i],f[i]);
	}
	printf("%d\n",f[n]);*/
}