Numerical Sequence (Hard vision) 题解
The only difference between the easy and the hard versions is the maximum value of \(k\).
You are given an infinite sequence of form "112123123412345…" which consist of blocks of all consecutive positive integers written one after another. The first block consists of all numbers from \(1\) to \(1\), the second one — from \(1\) to \(2\), the third one — from \(1\) to \(3\), …, the i-th block consists of all numbers from \(1\) to \(i\).
So the first \(56\) elements of the sequence are "11212312341234512345612345671234567812345678912345678910". Elements of the sequence are numbered from one. For example, the \(1\)-st element of the sequence is \(1\), the \(3\)-rd element of the sequence is \(2\), the \(20\)-th element of the sequence is \(5\), the \(38\)-th element is \(2\), the 56-th element of the sequence is \(0\).
Your task is to answer \(q\) independent queries. In the i-th query you are given one integer ki. Calculate the digit at the position ki of the sequence.
有一个无限长的数字序列,其组成为1 1 2 1 2 3 1.......1 2 ... n...,即重复的1 ~ 1,1 ~ 2....1 ~ n,这个数列连起来成为一个串,每位数字算一个元素,求第k(k<=1e18)个元素是什么
输入格式
The first line of the input contains one integer \(q(1≤q≤500)\) — the number of queries.
The i-th of the following q lines contains one integer \(k_i (1≤k_i≤10^{18})\) — the description of the corresponding query.
输出格式
Print q lines. In the i-th line print one digit \(x_i (0≤xi≤9)\) — the answer to the query i, i.e. xi should be equal to the element at the position ki of the sequence.
样例输入1
5
1
3
20
38
56
样例输出1
1
2
5
2
0
样例输入2
4
2132
506
999999999999999999
1000000000000000000
样例输出2
8
2
4
1
题解
首先把原数列变成这样:
1
12
123
1234
12345
123456
1234567
12345678
123456789
12345678910
1234567891011
123456789101112
12345678910111213
1234567891011121314
你会发现,这个形状抽象以下就是这样:
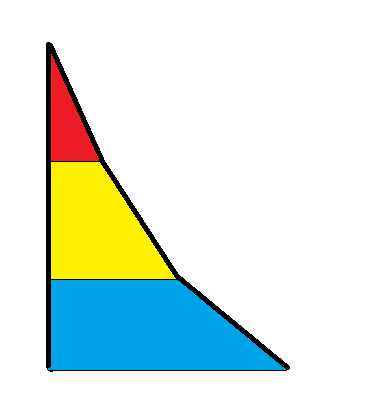
当然每一块实际上不是等高的,这个斜边斜率之所以会改变,是因为其最后一个数字位数不同,在第一块,每一行增加一位,第二组每一行增加2位...
我们只需要事先预处理出每块含数字的数量,然后拿到\(k\)以后,进行二分就能找到\(k\)在哪一块.
那么怎么预处理呢?
首先已知:
-
第一块第一行是1个数字
-
第一块每行增加\(1\)个,第二块每行增加\(2\)个,第三行每行增加\(3\)个,第\(i\)块每行增加\(i\)个,设为\(d_i\)
-
第一块有\(9\)行,第二块有\(90\)行,第三块有\(900\)行,第\(i\)块有\(9 \times 10^{i-1}\),设为\(l_i\)
那就可以用等差数列求和公式预处理
注意,每一块都有自己的通项公式,描述该块内第几行有多少数字
那么现在求每一块内数字数量的问题就变成了 已知首项和公差,求前\(n\)项和.
首项由前一块的通项公式得出,公差为\(d_i\), 由\(n=l_i\)可以求出该块数字数量,保存下来.
找到在哪一块之后,\(k\)减去前面所有块的数字数量,然后二分找到哪一行,每一行的数量由该块通项公式得出.
找到在哪一行之后,进行和以上类似的操作
比如这一行是
1
12
123
1234
12345
123456
1234567
12345678
123456789
12345678910
1234567891011
123456789101112
是不是似曾相识?

又是这个图,还是分块,分成1位数,2位数,3位数若干块(若干公差不同的等差数列),找到\(k\)在哪一块,然后枚举即可.
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 10;
long long a[15], b[15], c[15], T, n;
int main() {
for (int i = 1; i <= N; i++) {
long long x = i, l = 1, r = 0;
while (x--) l *= 10, r = r * 10 + 9;
l /= 10;
a[i] = (r - l + 1) * i;
b[i] = b[i - 1] + a[i];
c[i] = c[i - 1] + (b[i - 1] + i + b[i]) * (r - l + 1) / 2;
}
scanf("%lld", &T);
while (T--) {
scanf("%lld", &n);
long long pos = lower_bound(c + 1, c + N + 1, n) - c, l = 1, r = 0,
x = pos, t;
n -= c[pos - 1];
t = b[pos - 1];
while (x--) l *= 10, r = 10 * r + 9;
l /= 10;
long long L = l;
while (l <= r) {
int mid = (l + r) >> 1, cnt = mid - L + 1;
if ((2 * t + pos + cnt * pos) * cnt / 2 >= n)
r = mid - 1;
else
l = mid + 1;
}
long long cnt = l - L;
n -= (2 * t + pos + cnt * pos) * cnt / 2;
pos = lower_bound(b + 1, b + N + 1, n) - b;
n -= b[pos - 1];
long long ans = 1;
for (long long i = 1; i < pos; i++) ans *= 10;
t = (n - 1) / pos;
n -= t * pos;
ans += t;
n = pos - n;
while (n--) ans /= 10;
printf("%lld\n", ans % 10);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号