【cs231n】lecture 4 课程笔记

课程四 反向传播和神经网络

key： 反向传播 梯度 神经网络

---

Backpropagation 反向传播

1.概述：使用高等数学中求偏导的链式法则，对由损失函数正向计算得到的结果（用计算图表示），从后向前计算，求得损失函数中任一变量的梯度值；实为链式法则的递归调用；

2.为什么是梯度（导数）：梯度由导数计算而来，导数代表了某一点函数值的变化方向，想要使损失函数的最总结果变小，就需要清楚每一个参数（任一变量）的影响程度和变化程度；

3.计算图：将表达式以节点和线段表示，如图（可以给中间节点or结果以临时名字，方便表示和计算）

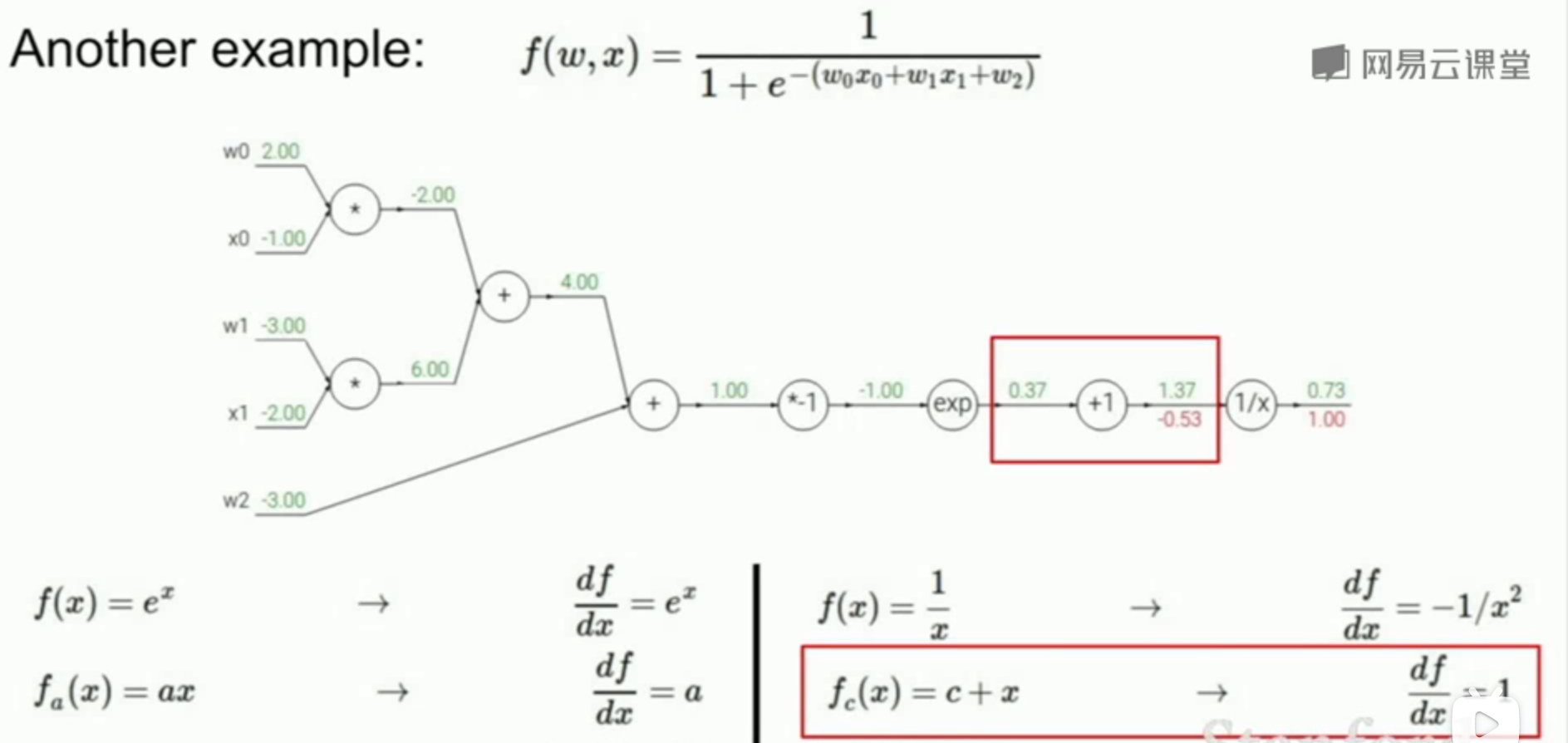
4.举例：较为复杂的函数（这里都尽量把每个节点都分为两个输入，三个或多个也可以，只要符合表达式即可），注意在从前往后计算时，要把正向计算的复杂式子看作整体（求偏导时），只用其损失函数的结果值

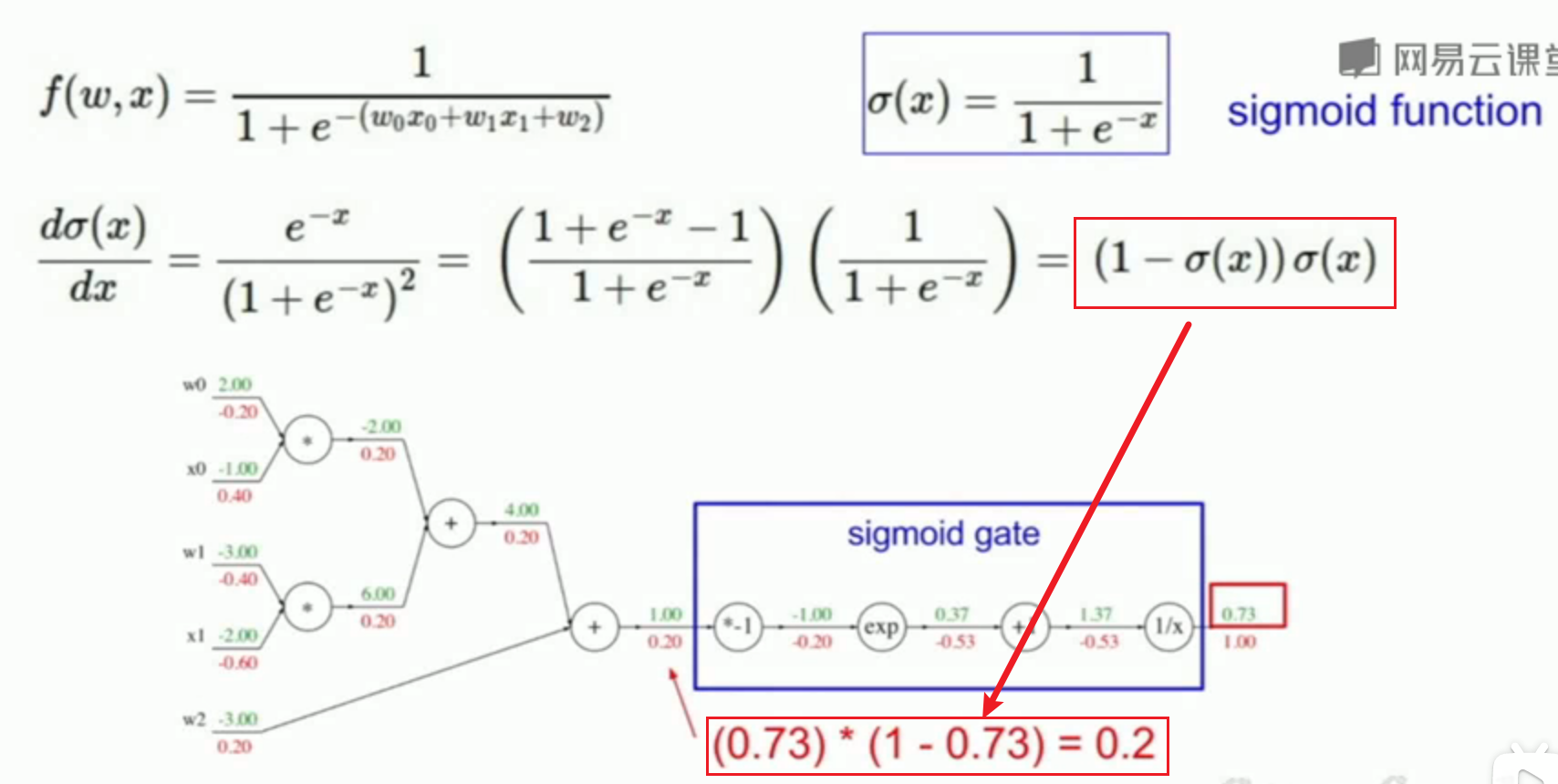
5.一个技巧：在面对复杂公式时，若数学上可以进行简化计算，可以应用

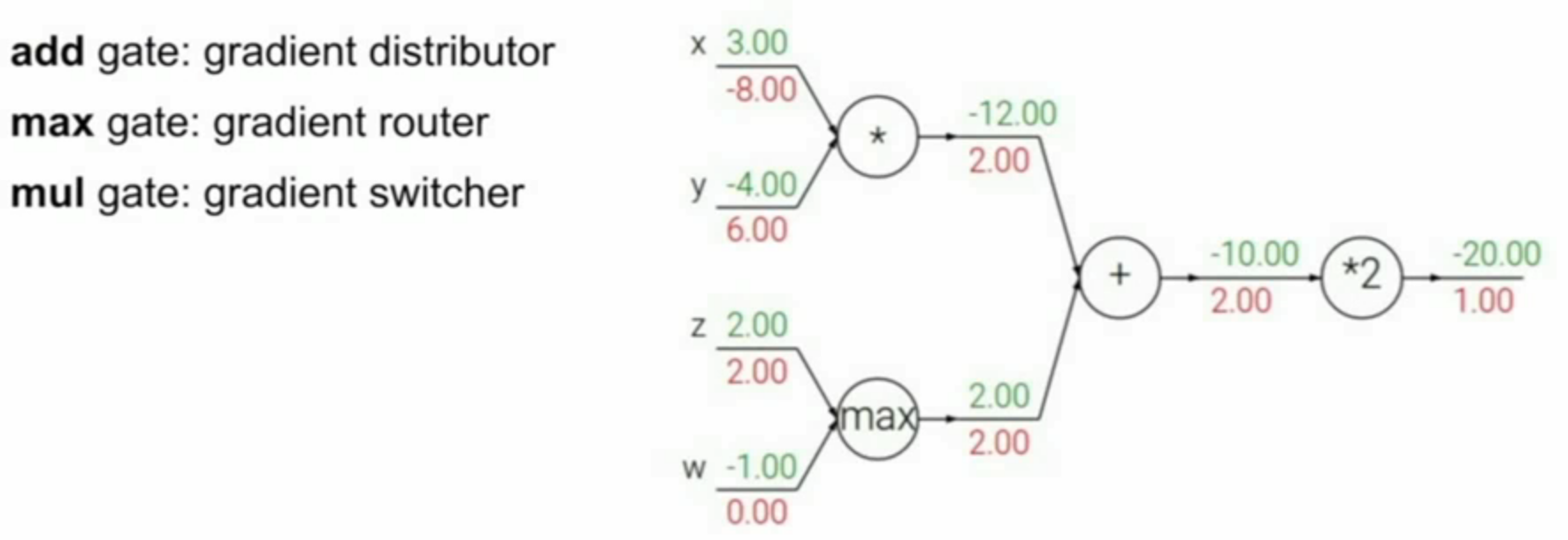
6.角色与功能：

• 加法（add gate）：梯度分发者，只传递，不改变梯度值
• 取最大（max gate）：梯度路由器，取到回传的梯度值后只分给其中一个输入支路
• 乘法（mul gate）：梯度转换器（放缩器），会根据两个（举例）输入分支的损失函数值相互影响（按比例放缩，此处比例是回传的梯度值）
  

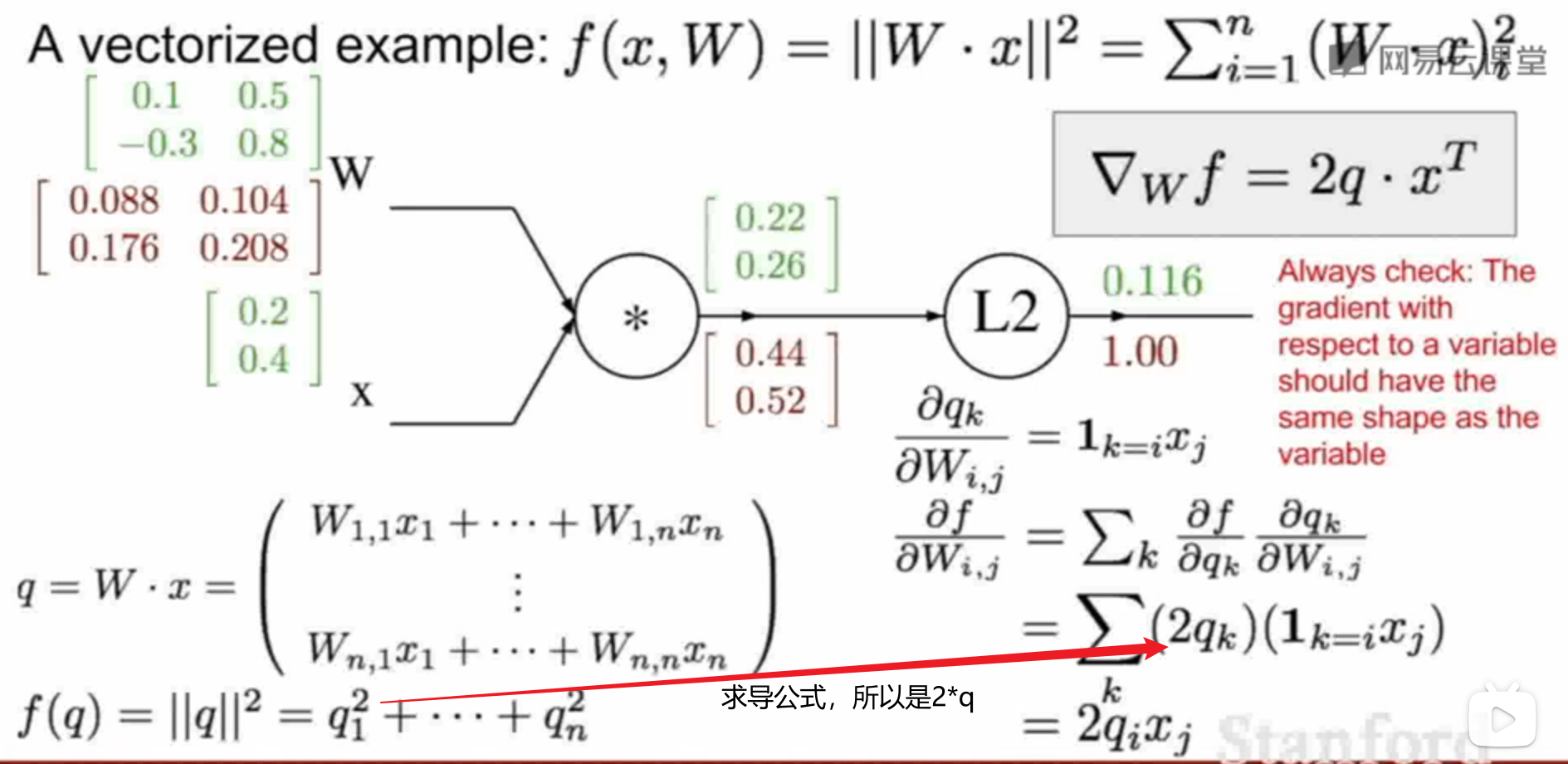
7.高维情况：高维时用向量和矩阵表示，求偏导的表达式被称为Jacobian matrix（雅各比矩阵）；此处的例子可以细看视频讲解；例子中的 L2 即求点积的模的平方

• 第一步 画计算图
• 第二步 正向计算
• 第三步 反向传播
  

8.实际应用：都有现成的模块化的API

---

神经网络

1.概述：如上 f = W * x ，f是输出层，w是一层网络，x是输入层，是线性的；两层网络时，用一个取最大将两层连起来，形成神经网络；三层如是

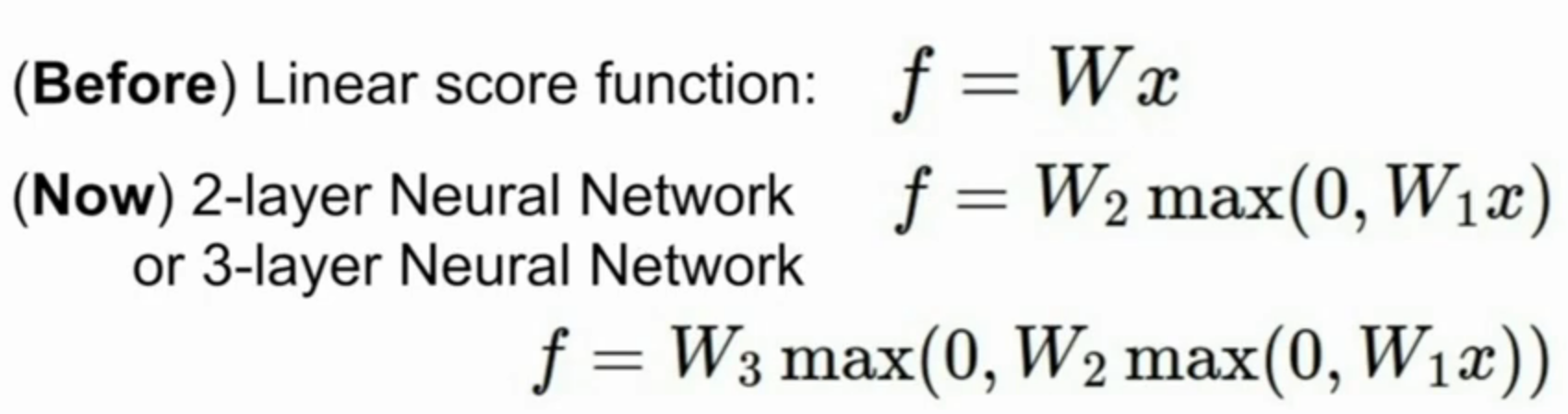
2.激活函数：对应神经元的放电率

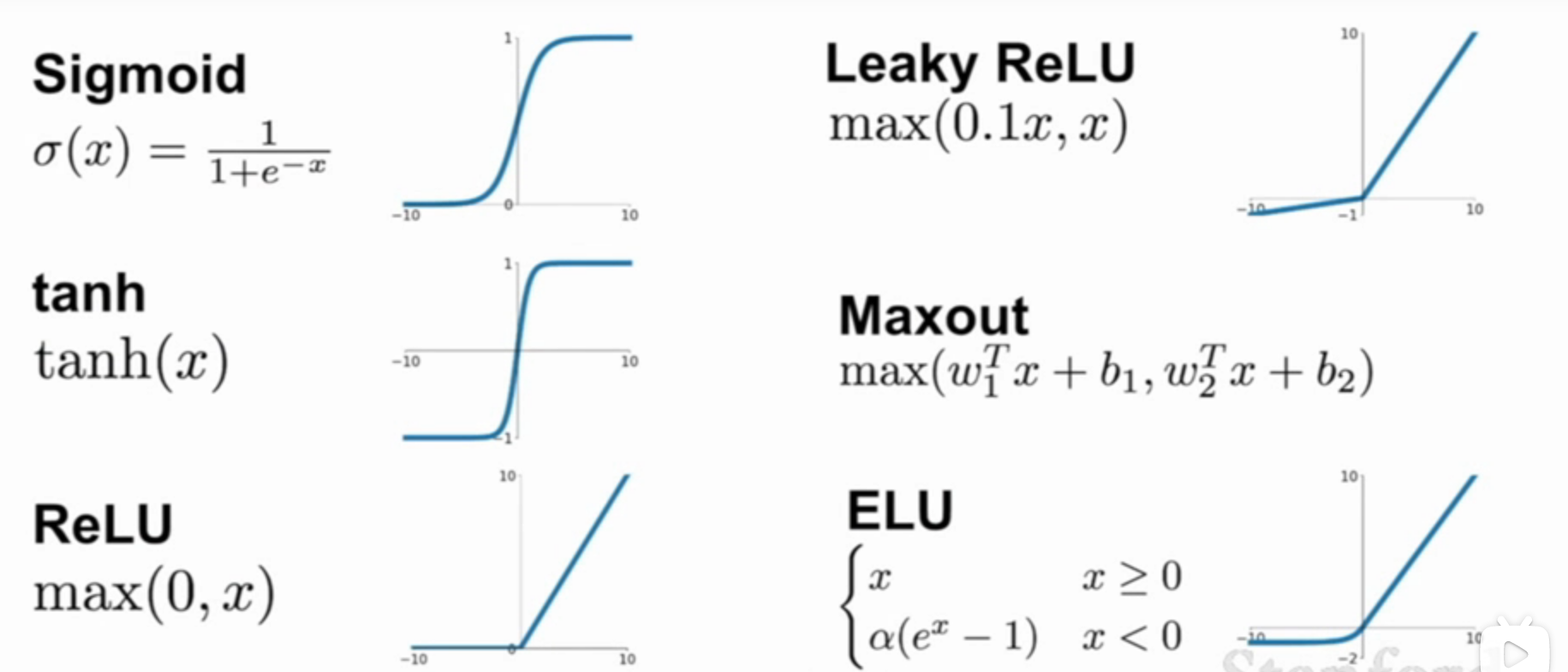
3.层数：通常是中间层（隐藏层） + 输出层，如两层神经网络or一隐藏层神经网络