论文阅读 2025-11-20: STLGame

这次的文章是《STLGame: Signal Temporal Logic Games in Adversarial Multi-Agent Systems》是2025年L4DC的文章。文章网站是https://sites.google.com/view/stlgameext

文章的主要目标是综合出一个能够提供给无人系统在未知敌对环境中去完成STL任务的控制策略(synthesize a robust and safe policy for autonomous systems under signal temporal logic (STL) tasks in adversarial settings against unknown dynamic agents). 标题里面的"STLGame"就是文章为了解决上面的问题而提出的一种框架, 它将多智能体系统博弈建模为一个两人零和博弈, 其中一个的目标是最大化STL 满意程度, 另一个, 相对地, 目标就是最小化STL满意程度. STLGame的目标是针对刚刚提到的哪一种博弈, 找到纳什均衡的policy profile.

1. Introduction

无人系统执行的任务往往会有严格的时间逻辑约束. 这种任务可以非常自然地通过STL, 信号时序逻辑来描述. 在这个工作中, 所有智能体的任务都由stl来描述. 并且希望能够综合出一种针对stl任务的控制策略. 主要难点在于所有智能体, 不论是己方的还是敌对的, 都共享一个环境, 并且对彼此是没有先验信息的.

STLGame把上面的问题建模为一个二人零和随机博弈, 己方agent目标就是最大化STL满意程度, 敌对的agent目标是最小化STL满意程度. STLGame的目标是给己方agent求得一个纳什均衡(NE)的控制策略. 使用纳什均衡的好处是能够在未知的情况下保证最好的预期(best case expected return). 不过这样的构想也不尽是完善的, 因为情况可能有很多种, 敌对agent的目标不是最低化我们的目标, 而是有可能有别的目标, 因此这个模型还是偏保守和局限的. 但这样的建模恰恰在没有先验信息的情况下能够提供最安全和稳健的solution.

STLGame的目标是求解得到一个纳什均衡策略对. 但是在连续动作空间里很难收敛到纳什均衡. 这项工作里主要是采用了classic Fictitious Play来求解, 这个方法可以被证明能在二人零和博弈中收敛到纳什均衡.

2. Problem Formulation

2.1 Signal Temporal Logic

\[\phi ::= \mathrm{True} \mid \pi^{\mu} \mid \neg \phi \mid \phi_1 \wedge \phi_2 \mid \phi_1 \mathbf{U}_{[a,b]} \phi_2, \tag{1} \]

其中, STL定性语义(Qualitative Semantics)定义如下, 我们使用 \((\mathbf{s},k)\models\phi\) 来表示 \(\mathbf{s}\) 在时刻 \(k\) 满足 \(\phi\).

\[\begin{aligned} (\mathbf{s}, k) \models \pi^{\mu} & \Longleftrightarrow \mu(s_k) \geq 0, \quad (\mathbf{s}, k) \models \neg \phi \Longleftrightarrow (\mathbf{s}, k) \not\models \phi, \\ (\mathbf{s}, k) \models \phi_1 \wedge \phi_2 & \Longleftrightarrow (\mathbf{s}, k) \models \phi_1 \text{ and } (\mathbf{s}, k) \models \phi_2, \\ (\mathbf{s}, k) \models \phi_1 \mathbf{U}_{[a,b]} \phi_2 & \Longleftrightarrow \exists k' \in [k+a, k+b], \text{s.t. } (\mathbf{s}, k') \models \phi_2 \text{. and } (\mathbf{s}, k'') \models \phi_1, \forall k'' \in [k, k']. \end{aligned} \]

除了定性语义, 用另一种说法是布尔语义, 之外, 还可以使用STL定量语义, 更简洁的说法是robustness, 这个数值能够用来衡量任务规范 \(\phi\) 的满足程度或者违反程度. 定义如下:

\[\begin{gathered} \rho^{\mathrm{True}}(\mathbf{s}, k) = \infty, \qquad \rho^{\pi^{\mu}}(\mathbf{s}, k) = \mu(\mathbf{s}_k), \\ \rho^{\neg \phi}(\mathbf{s}, k) = -\rho^{\phi}(\mathbf{s}, k), \qquad \rho^{\phi_1 \wedge \phi_2}(\mathbf{s}, k) = \min(\rho^{\phi_1}(\mathbf{s}, k), \rho^{\phi_2}(\mathbf{s}, k)), \\ \rho^{\phi_1 \mathbf{U}_{[a,b]} \phi_2}(\mathbf{s}, k) = \max_{k' \in [k+a, k+b]} \min(\rho^{\phi_2}(\mathbf{s}, k'), \min_{k'' \in [k, k']} \rho^{\phi_1}(\mathbf{s}, k'')). \end{gathered} \]

2.2 Stochastic Game

\(G = (\mathcal{N}, S, A, f, r, \rho_0, T, \gamma)\) 是一个N个agent的随机博弈. 运行流程一言以蔽之, 在时间步t, 博弈里面每一个agent i 根据其对应的控制策略 \(\pi^i\in \Pi^i : \sum_{a^i\in A^i}\pi^i(a^i\mid s)=1\) 来选择一个action \(a^i_t\), 然后多个agent的action合成一个joint action \(a_t = \times_{i \in \mathcal{N}} a_t^i\) 并且作用到动态系统中.

\[s_{t+1} = f(s_t, a_t), \tag{2} \]

定义历史信息 \(\hat{h}_t=\{(s_\tau,o_\tau,a_\tau)^{t-1}_{\tau=0},s^t,o^t\}\), 用 \(\sigma(\hat{h})\) 来表示observation的history. 在已知joint policy profile \(\pi=\langle \pi^i, \pi^{-i} \rangle\) 的情况下, 可以定义两个value function V和Q:

\[\begin{align} V_{\pi}^i(\hat{h}) &= \sum_{a \in A} \pi(a \mid \sigma(\hat{h})) Q_{\pi}^i(\hat{h}, a), \tag{3} \\ Q_{\pi}^i(\hat{h}, a) &= r^i(s(\hat{h}), a, s') + \gamma \sum_{o' \in \mathcal{O}} \mathcal{O}(o'|a, s') V_{\pi}^i(\langle \hat{h}, a, s', o' \rangle), \text{ where } s' = f(s(\hat{h}), a), \tag{4} \end{align} \]

V和Q分别可以和强化学习中的state value与 action value对应起来. 在已知expected return \(U^i(\pi)\) 与其他agent控制策略 \(\pi^{-i}\) 的情况下, 可以定义 best response(BR) policy:

\[\mathcal{BR}(\pi^{-i}) := \arg\max_{\pi^i \in \Pi^i} U^i(\langle \pi^i, \pi^{-i} \rangle) \]

\[\mathcal{BR}_{\epsilon}(\pi^{-i}) := \{ \pi^i \in \Pi^i : U^i(\pi^i, \pi^{-i}) \geq U^i(\mathcal{BR}(\pi^{-i}), \pi^{-i}) - \epsilon \}. \]

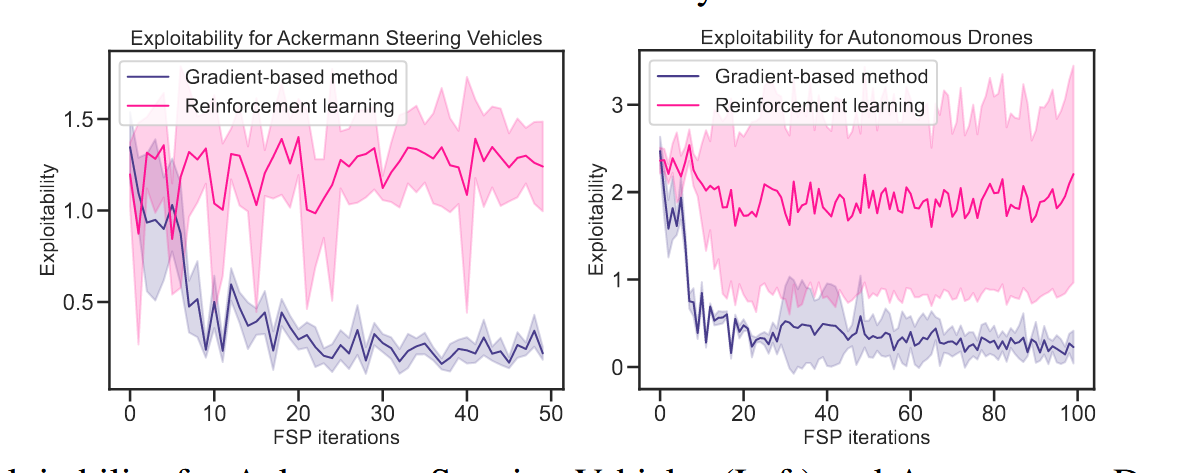
exploitability能够衡量当前策略和纳什均衡策略之间的距离

\[\mathcal{E}(\pi) := \sum_{i \in \mathcal{N}} \left( U^i(\mathcal{BR}(\pi^{-i}), \pi^{-i}) - U^i(\pi^i, \pi^{-i}) \right). \tag{5} \]

这里多做一些说明, 主要目标是求出一个足够让我们满意的己方agent控制策略 \(\pi^i\), 可以使用exploitability来描述这个控制策略的优异程度. 至于 \(\mathcal{BR}(\pi^{-i})\) 可能并不需要知道长啥样.

2.3 problem formulation

reward function定义如下:

\[r^1(s(\hat{h}_t), a, s') = \begin{cases} 0 & \text{if } t < T \\ \rho^{\phi}(\mathbf{s}) & \text{if } t = T \end{cases} \tag{6} \]

给定reward function之后, 文章主要研究的问题就可以定义服下:

Problem 1: 给定随机博弈G, STL 公式 \(\phi\) 以及动态系统 \(s_{t+1} = f(s_t, a_t)\), 要求求出 \(\pi^> {1,*}, \pi^{-1,*}\) 来满足下面的要求:

\[\pi^{1,*} = \operatorname*{arg\,max}_{\pi^1 \in \Pi^1} \min_{\pi^{-1} \in \Pi^{-1}} > \underset{\mathbf{s} \sim \pi}{\mathbb{E}} \rho^{\phi}(\mathbf{s}), \quad \pi^{-1,*} = > \operatorname*{arg\,min}_{\pi^{-1} \in \Pi^{-1}} \max_{\pi^1 \in \Pi^1} \underset{\mathbf> {s} \sim \pi}{\mathbb{E}} \rho^{\phi}(\mathbf{s}), \tag{7} \]

可以看出这是一个minimax的要求

3. Methods

STLGame 采用的是一种非常经典的Fictitious Play的方法来进行求解的. 轮到次序的agent分别进行一次次的博弈, 每次有agent参与博弈时, 参与的一方采用best response policy , 其他的则采用average policy. 在第k次循环中, 轮到次序的agent i计算出针对其他agent其对应的best response policy \(\beta_{k+1}^i\), 然后更新自己的average policy

\[\pi_{k+1}^{i} = \frac{k}{k+1} \pi_{k}^{i} + \frac{1}{k+1} \beta_{k+1}^{i}. \tag{8} \]

上面时对fictitious play的概述. 这个算法在我们这个场景下面的主要问题是:怎么计算出best response policy呢? 尤其是在带有连续动作空间的环境中! 那为了缓解这个问题呢, 文章使用了更加普遍化的一种fictitious play, 在这种fp中, 可以使用近似的best response和受扰动的average policy, 来近似达到纳什均衡.

\[\pi_{k+1}^{i} \in (1 - \alpha_{k+1}) \pi_{k}^{i} + \alpha_{k+1} (\mathcal{BR}_{\epsilon_k}(\pi_{k}^{-i}) + M_{k+1}^{i}), \forall i \in \{1, -1\}, \]

\[s.t. \lim_{k \to \infty} \sup_{j} \left\{ \left\| \sum_{l=k}^{j-1} \alpha_{l+1} M_{l+1} \right\| s.t. \sum_{l=k}^{j-1} \alpha_{l+1} \leq J \right\} = 0, \forall J \geq 0. \]

在实际工作中, 可以令 \(\alpha_k=\frac{1}{k}\), \(\epsilon_k=0\), \(M_k=0\)

3.1 Best Response的求解方法

算法中最重要的就是计算best response. 在STLGame的框架中, 每次迭代需要计算出最优的控制策略,也就是best response. 这种计算是在给定其他agent采用的未知average policy \(\pi_k^{-1}\) 情况下进行的. 这样, 求解best response可以概括为下面的problem:

Problem 2 给定随机博弈G, STL 公式 \(\phi\), 动态系统 \(s_{t+1} = f(s_t, a_t)\), 其他agent采用一个未知的policy \(\pi_k^{-1}\). 要求求出一个最优的控制策略, 能够最大化STLrobustness \(\pi_{k}^{1,*} = \arg \max_{\pi_{k}^{1} \in \Pi^{1}} \mathbb{E}_{\mathbf{s} \sim \langle \pi_{k}^{1}, \pi_{k}^{-1} \rangle} \rho^{\phi}(\mathbf{s})\)

由于对手有一个未知的policy, 因此采用例如MILP的classic方法来解决问题会比较受限, 因为在这一类方法中通常会假设能访问整个环境的精确模型.
但是是不是说明还是可以通过讲故事的方法引入classic approach?

也是因为这种原因, 文章不使用classic 方法, 可以通过和对手互动, 逐步加深对对手策略的理解, 在这些理解之上, 产生出一个近最优的策略. 基于这种思想呢, STLGame采用了强化学习近似求解best response.

STLGame使用了两种方法, 下面分别介绍一下.

首先是比较陈旧且平凡的RL方法, 就是每一次路径规划交互完成之后根据本次运行的reward来调整. 但是reward function是稀疏的, 在轨迹结束之前是获取不到stl robustness. 对于RL来说, 学习一个系数的reward还是太艰难了, 尤其是在连续动作空间下

那么为了解决上面的算法自身所带的一系列问题, 提高算法的性能表现, STLGame提出了第二种方法: Gradient-based Method. 其中使用了一种工具stlcg, 让agent不是一个只有最后给一次分数的reward, 二十一个可谓切随时间步逐步变化, 并且能够提供梯度方向的稠密信号(区别于稀疏信号). 在每一次训练迭代时, 部署策略网络, 计算全轨迹的robustness, 并通过反向传播和梯度下降来更新policy network

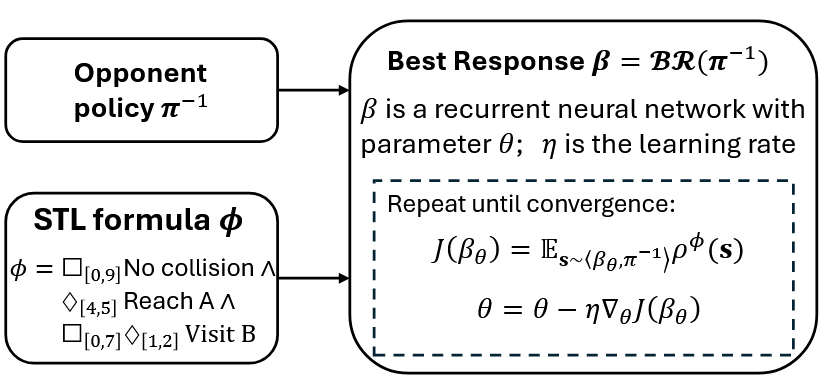
3.2 Average Policy

通过上面两种方法可以求agent的best response policy, 现在还有一个问题就是average policy 应该怎么求. 通常都是使用一个单独的随机神经网络, 然后用一个监督学习的方法来模拟ground-truth的平均策略.
在STLGame 的实验中, 发现用监督学习学习出来的网络效果并不好, 因此实际上使用的是average rule, 在已经有的BR policy set中根据概率采样.

这些policy, 从结构上来说他们需要所有的历史信息序列作为输入(原因是STL robustness需要所有历史信息作为输入来计算),因此使用的是RNN, 更具体一点就是LSTM

4. Experiments

文章针对两个控制对象进行了实验, 一个是阿克曼轮的小车, 另一个是三维空间的无人机, 各自进行二人零和随机博弈. 进行实验主要是为了回答三个问题:

1. 收敛性, 这个使用STLGame 能否学习到一个近似纳什均衡的策略呢?
2. 效率, STLGame的收敛速度是否有保证?
3. 鲁棒性, 在面对位置对手的情况下完成任务的成功率如何?

效率和收敛性都是挺程式化的实验内容了, 这边看一下曲线图瞬间就明白了

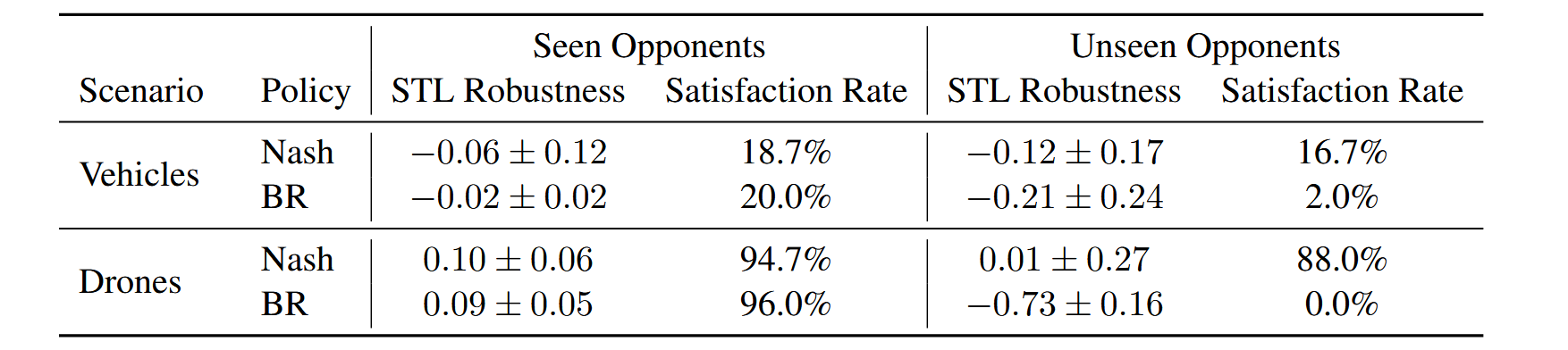
比较引人注目的是这个鲁棒性的测试, 这边policy类型分为Nash和BR. 其中nash就是在多轮FP中求出的最优秀的策略, 不是针对某个对手, 而是对所有历史对手的组合都是较为均衡的, 而BR就是固定对手策略, 为最大化自己STL robustness奖励而训练出的针对性最强的策略.