论文阅读2025.10.28:DEEPLTL: LEARNING TO EFFICIENTLY SATISFY COMPLEX LTL SPECIFICATIONS FOR MULTI-TASK RL

今天要讲的东西是2025 ICLR的文章，DEEPLTL: LEARNING TO EFFICIENTLY SATISFY COMPLEX LTL SPECIFICATIONS FOR MULTI-TASK RL

文章代码在https://deep-ltl.github.io/
要求的环境就是python3.10和pytorch2.2.2

文章主要贡献就是提出了一种能够处理长时序无限时域多任务的方法

1. 问题建模

1.1 强化学习 Reinforcement Learning

将强化学习的环境建模为马尔可夫决策过程(Markov decision processes ,MDPs)的框架， \(\mathcal{M}=(\mathcal{S},\mathcal{A},\mathcal{P},\mu,r,\gamma)\)，其中\(\mathcal{S}\)是状态空间,\(\mathcal{A}\)是动作空间集合, \(\mathcal{P}:\mathcal{S}\times\mathcal{A}\rightarrow\Delta(\mathcal{S})\) 表示现在还未知的转换内核(unknown transition kernel). \(\mu\in\Delta(\mathcal{S})\) 表示初始状态分布. \(r:\mathcal{S}\times\mathcal{A}\times\mathcal{S}\rightarrow\mathbb{R}\). \(\gamma\in[0,1)\) 是强化学习中比较常用的discount factor.

我们将采取动作\(a\)之后从状态\(s\)转换到\(s^{\prime}\)的概率记作\(\mathcal{P}(s^{\prime}|s,a)\).使用的策略\(\pi:\mathcal{S}\rightarrow\Delta(\mathcal{A})\)从当前的状态映射到动作的概率分布.系统的控制是时间触发的,因此在MDP中使用policy \(\pi\)就会形成一条轨迹:\(\tau=(s_0,a_0,r_0,s_1,a_1,r_1,...)\),其中\(s_0 \sim \mu, a_t \sim \pi(\cdot | s_t), s_{t+1} \sim \mathcal{P}(\cdot | s_t, a_t),r_t\sim r(s_t,a_t,s_{t+1})\)

强化学习的目标通常都是找到一种最优策略\(\pi^*\),能够最大化return \(J(\pi) = \mathbb{E}_{\tau \sim \pi} \left[ \sum_{t=0}^{\infty} \gamma^t r_t \right]\)

1.2 线性时序逻辑 Linear Temporal Logic,LTL

线性时序逻辑提供了一种能够描述无限时域轨迹规范的形式化语言.LTL公式是定义在一系列的原子命题上的,换言之就是给定原子命题,才能够进行LTL描述.LTL的语法可以简要展示为:

\[\mathbf{true} \mid a \mid \varphi \wedge \psi \mid \neg \varphi \mid \mathbf{X} \varphi \mid \varphi \mathbf{U} \psi \]

其中\(a\in AP\),并且\(\phi,\varphi\)都是LTL规范,\(\wedge,\neg\)是布尔运算符与,非.时序运算符\(\mathbf{X},\mathbf{U}\)分别表示"next"和"until",特别地,在时序逻辑中还有\(\mathbf{F}\)(eventually)和\(\mathbf{G}\)(always)两种运算符,但是他们都能用其他运算符间接地表示:$\mathbf{F} \varphi \equiv \mathbf{true} \mathbf{U} \varphi $ 与\(\mathbf{G} \varphi \equiv \neg \mathbf{F} \neg \varphi .\)

从语义上来说, LTL的满意程度是通过递归满意度关系\(w \models\varphi\)定义的. 我们通过labeling function \(L:\mathcal{S}\rightarrow2^{AP}\), 这个函数的输入时马尔可夫决策过程的状态,输出是所有原子命题的真伪值.给定一段MDP轨迹\(\tau\)之后, 能够映射到\(Tr(\tau)=L(s_0)L(s_1)L(s_2)...\)
因此使用policy\(\pi\)满足LTL规范\(\varphi\)的概率可以被定义为:\(\Pr(\pi \models \varphi) = \mathbb{E}_{\tau \sim \pi} [1[\tau \models \varphi]]\)

1.3 Buchi automata, BA

很多主流方法都是使用Buchi automata来处理LTL公式, 这是一种能够用来观察任务进程是否正在朝着正确的方向前进的自动机. 特别地, 在DEEP-LTL这篇文章中使用的是limit-deterministic Buchi automata (LDBAs). 这样一种经过特化的自动机特别适合搭配MDP一块使用. 一个LDBA通常使用元组 \(\mathcal{B}=(\mathcal{Q},q_0,\Sigma,\delta,\mathcal{F},\mathcal{E})\) 来表示. 其中 \(\mathcal{Q}\) 是一个有限的状态集合. \(q_0\in \mathcal{Q}\) 表示初始状态, \(\Sigma=2^{AP}\) 是一个有限的alphabet, 能够表示原子命题的真伪. \(\delta:\mathcal{Q}\times(\Sigma \cup\mathcal{E})\rightarrow\mathcal{Q}\) 是转换函数. \(\mathcal{F}\) 表示可接受状态的合集. 这边 \(\mathcal{Q} = \mathcal{Q}_N \uplus \mathcal{Q}_D\) ,是两个不相交的子集组成(分为确定区域和不确定区域), \(\mathcal{F} \subseteq \mathcal{Q}_D \text{ and } \delta(q, \alpha) \in \mathcal{Q}_D \text{ for all } q \in \mathcal{Q}_D \text{ and } \alpha \in \Sigma.\) 集合 \(\mathcal{E}\) 是一组带索引的 \(\varepsilon\)-transitions, 他们从 \(\mathcal{Q}_N\) 转换到 \(\mathcal{Q}_D\), 并且不消耗任何输入,并且同时没有其他转换关系能从 \(\mathcal{Q}_N\) 转换到 \(\mathcal{Q}_D\), 从直观上来说, 就是不依赖任何环境输入, 也不消耗事件或动作的状态转换

一个Buchi automata \(\mathcal{B}\) 的运行过程 \(r\), 通过 \(\omega\)-word 描述的 \(w\in(2^{AP})^\omega\) 是状态集合 \(\mathcal{Q}\) 中状态的无限序列. 如果 \(w\) 上存在 \(\mathcal{B}\) 的运行 \(r\), 并且能够无限频繁地访问可接受状态, 则表示 \(w\) 是可以被接受的. 对于任意一个LTL公式 \(\varphi\), 可以构造 LDBA \(\mathcal{B}_{\varphi}\), 来判断一个进程是否满足规范 \(\varphi\)

这边就有一个问题了:为什么要使用LDBA而非BA?

1.4 乘积MDP(Product MDP)

乘积MDP \(\mathcal{M}^\varphi\) 由MDP \(\mathcal{M}\) 和 LDBA \(\mathcal{B}_\varphi\) 乘积而成, 能够同步执行 \(\mathcal{M}\) 和 \(\mathcal{B}_\varphi\), 拥有状态空间 \(\mathcal{S}^\varphi=\mathcal{S}\times\mathcal{Q}\), 动作空间 \(\mathcal{A}^\varphi=\mathcal{A}\times\mathcal{E}\), 初始状态分布 \(\mu^\varphi(s,q)=\mu(s)\cdot\mathcal{1}[q=q_0]\) 与转换函数

\[\mathcal{P}^\varphi((s', q') | (s, q), a) = \begin{cases} \mathcal{P}(s' | s, a) & \text{if } a \in \mathcal{A} \wedge q' = \delta(q, L(s)), \\ 1 & \text{if } a = \varepsilon_q \wedge q' = \delta(q, a) \wedge s' = s, \\ 0 & \text{otherwise.} \end{cases} \]

需要注意的是, 这样一个乘积马尔可夫决策过程能够让我们在考虑动作的同时关注LDBA, 但是实际使用中并不会直接构建乘积MDP. 而是简单地在每个时间步观察到的状态 \(s\), 映射成当前的原子命题状态 \(L(s)\), 更新当前的LDBA状态 \(q\). \(\mathcal{M}^\varphi\) 中的轨迹是序列 \(\tau=((s_0,q_0),a_0,(s_1,q_1),a_1,...)\), 同时我们把 \(tau\) 映射到LDBA状态的轨迹 \(\tau_q=(q_0,q_2,...)\), 这样公式 \(\varphi\) satisfaction probability可以表示为:

\[\Pr(\pi \models \varphi) = \mathbb{E}_{\tau \sim \pi} [\mathbb{1}[\inf(\tau_q) \cap \mathcal{F} \neq \emptyset]], \]

这边 \(\inf(\tau_q)\) 表示 \(\tau_q\) 中出现无数次的状态集合

1.5 Problem Formulation

主要的目标是找到一个specification-conditioned policy \(\pi\mid\varphi\), 即给定任务规范, 能够计算出最大化满足规范 \(\varphi\) 的最优策略

\[\pi^* = \arg\max_{\pi} \underset{\substack{\varphi \sim \xi, \\ \tau \sim \pi|\varphi}}{\mathbb{E}} [1[\tau \models \varphi]]. \tag{1} \]

可以通过goal-conditioned reinforcement learning来在乘积MDP中获得最优策略, 给定LTL公式的概率分布 \(\xi\), 采样得到LTL公式 \(\varphi \sim \xi\) 与轨迹 \(\tau\sim\pi\mid\varphi\), 如果policy能够引导到accepting states, 就给予奖励1, 否则就给0. 而在实际上, 我们往往更加关注效率, 即是否使用更少的步数来满足任务要求, 即使他们满足任务的概率没有达到最高. 下面给出完整的问题描述:

Efficient LTL satisfaction: 给定一个未知的 MDP \(\mathcal{M}\), LTL公式的概率分布 \(\xi\), 采样得到的LTL公式 \(\varphi\), 对应的LDBA \(\mathcal{B}_\varphi\), 需要给出最优策略:

\[\pi^* = \arg\max_{\pi} \underset{\substack{\varphi \sim \xi, \\ \tau \sim \pi|\varphi}}{\mathbb{E}} \left[ \sum_{t=0}^{\infty} \gamma^t 1[q_t \in \mathcal{F}_{\mathcal{B}_{\varphi}}] \right]. \tag{2} \]

2. 求解方法

主要想法是使用推断可能满足给定任务规范的路径, 从LDBA中提取出有用的 \(q\). 之后该表示用于调节策略, 引导智能体朝着满足给定的任务规范的方向去.

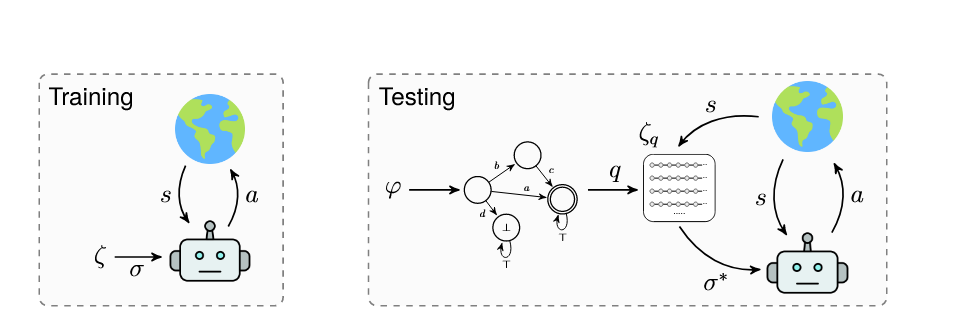
2.1 将LTL规范表示为序列 Representing LTL Specification as Sequences

首先使用深度优先搜索算法(Depth-first Search, DFS), 找到所有从 \(q\) 出发到达可接收状态 \(q_f\in\mathcal{F}\) 的路径. 并且使用 \(P_q\) 表示这些路径的集合.

给定一条无限序列的路径 \(p=(q_1,q_2,...)\in P_q\), 令 $ A_{i}^{+} = { a : \delta(q_i, a) = q_{i+1} }$ 表示那些能够让当前状态 \(q_i\) 朝着满足目标的状态 \(q_{i+1}\) 推进的命题集合, 注意这里的 \(a\) 并不是MDP中的动作, 而是原子命题真伪表示, 即 \(a\in 2^{AP}\), 而无法做到此效果的命题集合表示为 $ A_{i}^{-} = { a \notin A_{i}^{+} \wedge \delta(q_i, a) \neq q_i }$. 为了让策略能够生成满足LTL规范的路径, 需要让每个时间步的MDP状态 \(s_{t_i}\) 满足 \(L(s_{t_i})\in A_i^{+}\), 同时避免 \(A_i^-\) 中的元素.

我们令 \(\sigma_p=((A_{1}^{+}, A_{1}^{-}), (A_{2}^{+}, A_{2}^{-}), \dots)\) 表示与 \(p\) 对应的reach-avoid 序列. 并把所有 \(p\) 对应的序列的集合表示为 \(\zeta_q = \{ \sigma_p : p \in P_q \}\)

2.2 主要方法介绍

在训练阶段, 学习一个常规的基于序列的policy \(\pi:\mathcal{S}\times\zeta\rightarrow\Delta(\mathcal{A})\) 和一个value function \(V^{\pi}:\mathcal{S}\times\zeta\rightarrow\mathbb{R}\) 来满足定义在原子命题集合\(AP\)上的任意reach-avoid sequence \(\sigma\in\zeta\).

在训练过程中, 我们会使用当前的LDBA状态\(q\), 根据value function选择最优的reach-avoid sequence来满足 \(\varphi\).

\[\sigma^* = \arg\max_{\sigma \in \zeta_q} V^{\pi}(s, \sigma). \tag{3} \]

训练完成之后, 就根据 \(a\sim\pi(\cdot ,\sigma^*)\) 来采取行动直到下一个LDBA状态.

\[\sigma = ((A_{1}^{+}, A_{1}^{-}), (A_{2}^{+}, A_{2}^{-}), \dots) \xrightarrow{\mathbf{DeepSets}} (e_{A_{1}^{+}} \| e_{A_{1}^{-}}, e_{A_{2}^{+}} \| e_{A_{2}^{-}}, \dots) \xrightarrow{\mathbf{RNN}} e_{\sigma} \]

测试过程就是在乘积MDP中执行策略 \(\tilde{\pi}\). 下面介绍模型的架构, sequence-conditioned policy, 并给出一个关于训练和测试的详细pipeline.

2.3 策略\(\pi\)的模型架构

使用模块化神经网络来作为序列条件测率\(\pi\)的参数, 其中包括一个观测模块(observation module), 一个序列模块(sequence module), 一个动作模块(actor module).

观测模块的主要作用是来获得环境的信息, 使用CNN作为网络的架构; 序列模块主要用来处理reach-avoid sequence, 对其进行编码, 通常使用RNN作为网络架构. actor module 使用MLP作为网络的架构, 用来处理上面两个模块的信息, 输出动作.

下面介绍sequence module.

第一步是对原子命题assignment进行编码. 使用DeepSets架构来获得一组assignment赋值\(A\)的编码 \(\mathbf{e}_A\). 用数学语言表示就是:

\[e_A = \rho \left( \sum_{a \in A} \phi(a) \right), \tag{4} \]

其中, \(\phi(a)\) 是一个需要去学习的embedding function, \(\rho\) 是一个需要去学习的非线性转换(a learned non-linear transformation).

第二步是对reach-avoid sequence进行编码. 在获得了reach-avoid 序列 \(\sigma\) 中每一个时间步的原子命题集合 \(A_i^+\) 与 \(A_i^-\) 的编码结果之后, 把这些embeddings连接起来, 过一个RNN, 就是我们这个模块的输出. 由于 \(\sigma\) 是一个无限的序列. 我们就用 \(\tilde{\sigma}=\sigma_{pre}+k*\sigma_{loop}\) 来近似它, 即一个有限prefix 序列的 \(\sigma_{pre}\) 和k次循环的 \(\sigma_{loop}\) 序列.

2.4 训练过程

Deep-LTL 使用goal-conditioned RL来训练policy \(\pi\) 和value function \(V^\pi\). 即在每次训练的 episode之前先生成一个随机的reach-avoid sequence, 并给定奖励. 具体来说, 给定一个训练的序列 \(\sigma = ((A_{1}^{+}, A_{1}^{-}), \dots, (A_{n}^{+}, A_{n}^{-}))\), 并通过一个index \(i\in[n]\) 来跟踪任务推进的进程. 如果在时间步\(t\)智能体满足了一个原子命题集合 \(A\), 即 \(L(s_t)\in A\). 如果智能体满足 \(A_i^+\), 就把index 增加一下. 如果index \(i=n+1\), 就给出reward 1, 并终止这个episode. 如果任何一个时间步满足了 \(A_i^-\), reward就变成-1, 其他情况就给出0作为reward. 使用的具体RL方法是PPO

此外, 为了提升策略的性能, 还使用了一种简单的课程学习curriculum learning, 也就是分成多个阶段来进行学习, 第一个阶段仅学习简单的任务规范, 之后逐渐变复杂.

2.5 对于\(\varepsilon\)-transition的处理方法

当自动机处于带有 ε-transition 的状态时，策略可以选择保持在当前状态，或执行一个“ε动作”直接跳转到下一个逻辑状态，而无需与环境交互。为此，DeepLTL 扩展了策略的动作空间，加入一个额外维度代表 ε-action；在离散动作空间中，直接增加一个新动作；在连续动作空间中，将 ε-action 的选择概率建模为混合连续/离散分布。当策略执行 ε-action 时，仅更新自动机状态，不影响环境状态。实际实现中，只有当当前状态标签不会导致立即失败时（即\(L(s)\notin A_2^-\)），才允许执行 ε-transition。

3. 实验

实验主要想探究的问题是:

• DeepLTL是否能够在没有先验的情况下(zero-shot)满足复杂的LTL规范?
• 与其他baseline相比性能和效率如何呢?
• 能否成功处理无限时域任务规范

实验的环境包括LetterWorld, ZoneEnv, Flatworld, 这些环境都是在LTL2Action中提出来的.

实验的baseline分别是LTL2Action和GCRL-LTL

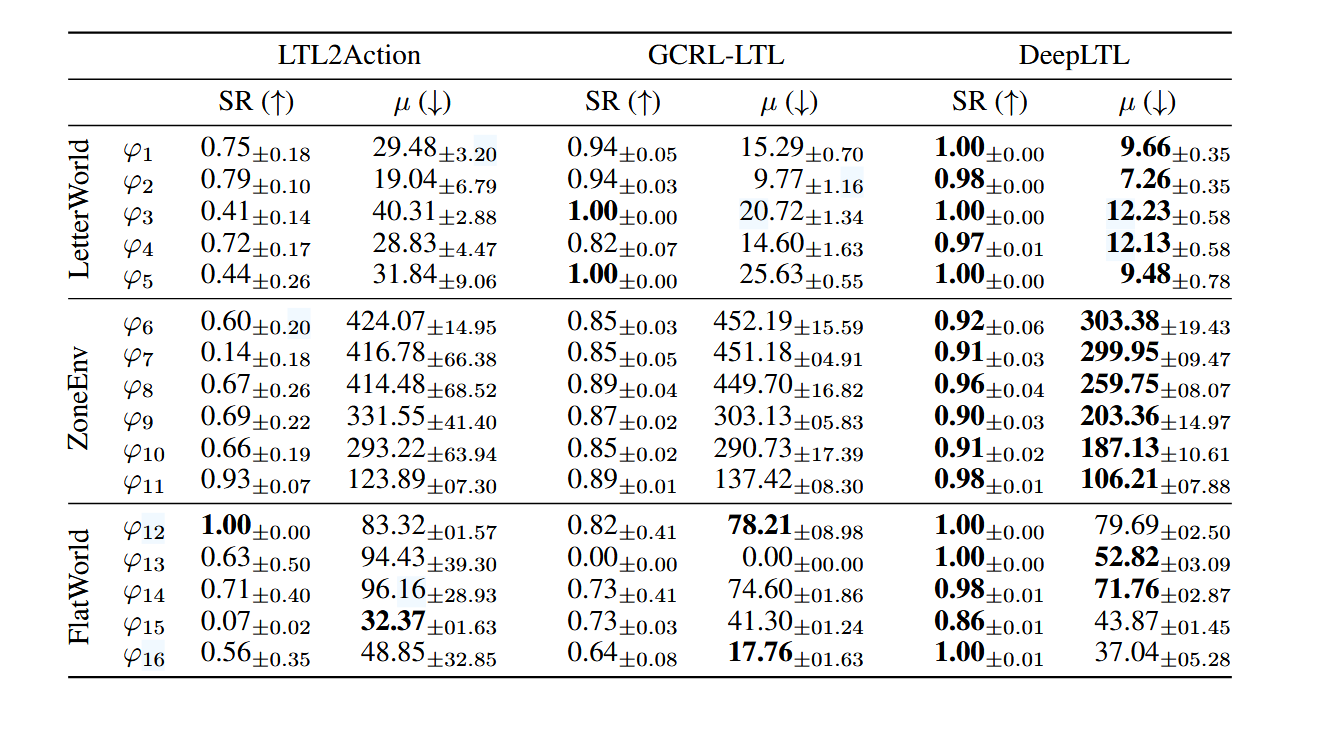
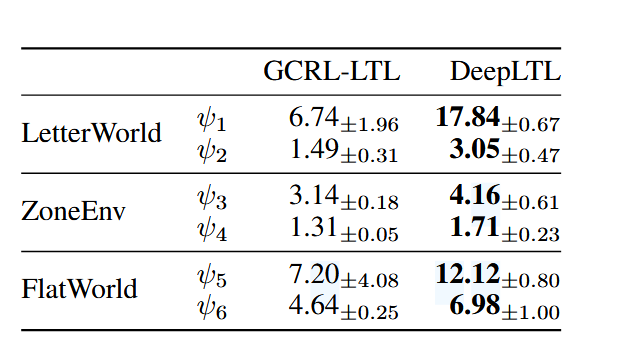
实验结果如下