图的深度优先遍历

深度优先遍历，也称作深度优先搜索，缩写为DFS
深度优先遍历从某个顶点出发，访问此顶点，然后从v的未被访问的邻接点触发深度优先便利图，直至所有和v有路径想通的顶点都被访问到。

这样我们一定就访问到所有结点了吗，没有，可能还有的分支我们没有访问到，所以需要回溯（一般情况下都设置一个数组，来记录顶点是否访问到，如果访问到就不执行DFS算法，如果未被访问过就执行DFS算法）

基本思路：

从图中某顶点v出发：

 1. 访问顶点v； 
 2. 依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问；
 3. 若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，
 直到图中所有顶点均被访问过为止。

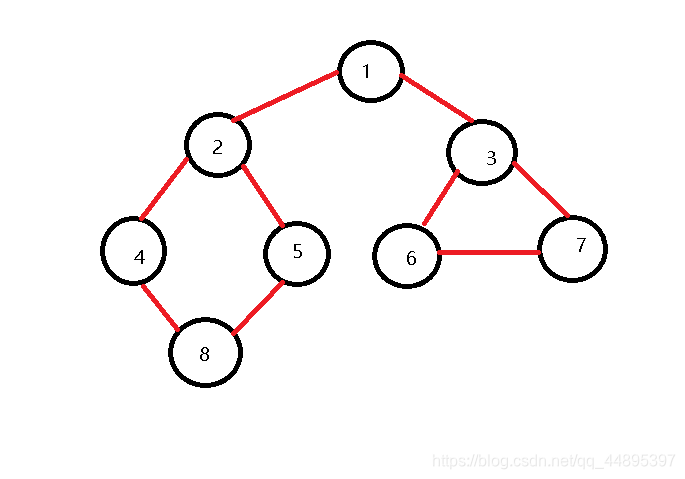
以下图为例：（以无向图为例）
该图的深度优先遍历结果应该为：1->2->4->8->5->3->6->7

代码实现：

	 //深度优先遍历
	    public void dfs() {
	        for (int i = 0; i < getNum(); i++) {
	            if (!isVisited[i]) dfs(isVisited, i);
	        }
	    }
	
	    private void dfs(boolean[] isVisited, int index) {
	        //输出该元素，把该元素标记为已被访问
	        //找到该元素的第一个邻接节点，如果该节点存在-->
	        // 1、该节点被访问过，找到该节点的下一个邻接节点
	        //2、该节点没有被访问过，直接递归到这个节点
	        //如果没有找到该节点（不存在邻接节点）-->重载直接进入下一个节点
	        System.out.println(getValueByIndex(index));
	        isVisited[index] = true;
	        int neibornode = getFirstNode(index);
	        while (neibornode != -1) {
	            if (!isVisited[neibornode]) dfs(isVisited, neibornode);
	            neibornode = getNextNode(index, neibornode);
	        }
	        dfs();
	    }
	
	    //找到莫个结点的第一个邻接节点
	    public int getFirstNode(int index) {
	        for (int i = 0; i < getNum(); i++) {
	            if (edge[index][i] > 0) return i;
	        }
	        return -1;
	    }
	
	    //找到莫个结点的下一个邻接节点
	    public int getNextNode(int v1, int v2) {
	        for (int i = v2 + 1; i < getNum(); i++) {
	            if (edge[v1][i] > 0) return i;
	        }
	        return -1;
	    }

代码实现结果：