Coprime
Coprime
前置芝士
莫比乌斯反演
正文
首先,我们来分析题意。
题目中给出 \(n\) 个人,每个人有一个编号 \(k\) ,要求我们从中选出 \(3\) 个人,三人编号分别为 \(k_a\) ,\(k_b\) ,\(k_c\) ,
使得这三个人的编号满足两两之间同时互质或不互质,最后求出所有满足上述式子的方案。
我们先来考虑:在什么时候,三个数之间的最小公倍数都相等呢?如果我们朴素一点地计算出答案,那么只要用三层循环,并判断条件是否成立,就可以得到答案。但是,这种朴素算法的时间复杂度为 \(O(n^3)\) ,但题目中的 \(n\) 的范围为 \(10^5\) ,所以这样的时间复杂度显然无法帮助我们拿到这道题的满分。
既然朴素算法的时间复杂度,那该如何更快地计算出这道题的答案呢?我们不妨从容斥的角度来考虑。
首先,从 \(n\) 个人中选出 \(k\) 个人,这表示我们最多能有 \(C_n^3\) 种选人方案。然后,我们随机选出三个人,将选出来的三个人之间两两连边,若两个人的编号互质,则连 ** 蓝边 **,若两人的编号不互质,则连 黄边 ,接着我们会发现,若要符合题目条件,我们只能有以下几种可能:
第一种: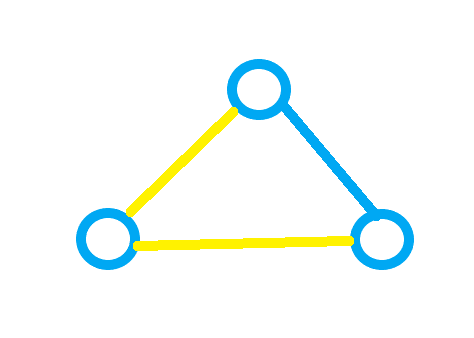
第二种: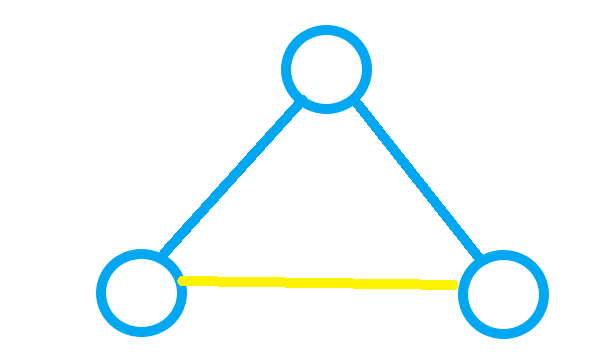
我们会发现两点:第一:最终所得的三角形的个数即为符合条件的方案数。第二:总有两个人身上有两种颜色的边。所以,我们现在定义一个函数 \(f\) ,\(f(i)\)表示与 \(i\) 互质的数有多少个。那么,在计算三角形个数(即总方案数)时,我们就不用再考虑三个人了,而是只要考虑一个人,不过我们在计算时只能取答案的一半,因为身上连有两条不同边的人有两个。
所以,我们有式子:
式中,\(f(i)\) 表示在范围内与 \(i\) 互质的数,所以 \((n-i-f(i))\) 即为范围内与 \(i\) 不互质的数,而 \(n\) 并非题目中的 \(n\) ,而是题目中的 \(a_i\) 的最大值 (即\(10^5\),接下来我们的 \(n\) 都为 \(10^5\) )。所以,我们只要能求出全部的 \(f(i)\) ,就可以很快地得到答案了。关于 \(f(i)\) ,我们可以通过下面的方法来处理。
在处理 \(f(i)\) 之前,我们先定义一个数组 \(a\) ,\(a_i\) 则表示数字 \(i\) 在数据中是否存在,若存在,则 \(a_i=1\) ,否则 \(a_i=0\)。然后,再根据我们定义的函数 \(f\) ,可以得到下面的式子:
这算的便是与 i 互质的数的个数了。我们可以继续加以推导:
然后我们再定义一个函数 \(g\) ,使得 \(g(d)\) =\(\sum_{d|i}^n a_i\) ,这样我们便可以对 \(g\) 进行预处理,从而降低时间复杂度。
预处理的代码如下:
for (int i=1; i<=n; i++) {
for (int j=i; j<=n; j+=i) g[i]+=a[j];
}
可见这个预处理的时间复杂度为 \(O(n \log n)\) 。
然后,对于 \(\mu\) 的处理,相信大家做到这道题的时候早就不陌生了,这里就直接采用线性筛的方法(其实没有必要)进行预处理了。然后,我们的 \(f\) 便能直接计算出来。然而,如果我们对每个 \(f\) 单独计算,那么时间复杂度就会变成 \(O(n \sqrt {n})\) ,但只要我们同时计算多个 \(f\) ,那么时间复杂度就会降到 \(O(n\log n)\) (关于时间复杂度的计算,请读者自行思考)。而同时处理多个 \(f\) 的也能很容易的实现,如果说原本我们应该枚举的是 \(x\) 的因数,那现在我们可以通过枚举 \(x\) 的倍数来进行优化。
代码如下:
for (int i=1; i<=n; i++) {
if (mu[i]==0) continue;
for (int j=i; j<=n; j+=i) {
if (a[j]==1) {
f[j]+=mu[i]*(g[i]-1);
}
}
}
最终,我们再将算出来的一切带入最初的式子,就可以计算出答案了。
完整代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100005;
int mu[N],prime[N],tot;
bool np[N];
ll f[N],g[N];
bool a[N];
void init(int n) {
mu[1]=1;
np[1]=1;
for (int i=2; i<=n; i++) {
if (!np[i]) {
mu[i]=-1;
prime[tot++]=i;
}
for (int j=0,k; (k=prime[j]*i)<=n; j++) {
np[k]=1;
if (i%prime[j]==0) {
mu[k]=0;
break;
}
mu[k]=-mu[i];
}
}
}
int main() {
int T;
init(100000);
//cout<<1<<endl;
scanf("%d",&T);
for (int _=0; _<T; _++) {
int n,z;
scanf("%d",&n);
z=n;
memset(g,0,sizeof g);
memset(f,0,sizeof f);
memset(a,0,sizeof a);
ll ans=0;
for (int i=1; i<=n; i++) {
int Now;
scanf("%d",&Now);
a[Now]=1;
}
n=100000;
for (int i=1; i<=n; i++) {
for (int j=i; j<=n; j+=i) g[i]+=a[j];
}
for (int i=1; i<=n; i++) {
if (mu[i]==0) continue;//优化
for (int j=i; j<=n; j+=i) {
if (a[j]==1) {
f[j]+=mu[i]*(g[i]-1);
}
}
}
for (int i=1;i<=n;i++) ans=ans+f[i]*(z-1-f[i]);
ans=(ll)z*(z-1)*(z-2)/6-ans/2;
printf("%lld\n",ans);
}
return 0;
}

