云智计划_数据结构_并查集

算法介绍

其实没什么好说的

注意几个点

1.fa[i]=i;

2.按秩合并(亦称启发式合并)与路径优化可以同时存在，只有一个复杂度为O(nlog n)，两个都用就是O(nα(n))，相当于O(n)

α()在1e6的数据下，也只有5，比常数还常数

代码

int find(int x){return(fa[x]==x?x:fa[x]=find(fa[x]));}

void marge(int a,int b)
{
    x=find(x);y=find(y);
    if(a==b)return ;
    else fa[a]=b;//实在复杂度就是差一点，可以写个按秩排序
}

基础例题

1.P1111 修复公路 - 洛谷

其实就是板子

并查集特征：只关心谁与谁在同一集合

知识点：离线处理

然后就没辣

Talk is cheap,show me the code

//https://www.luogu.com.cn/problem/P1111
//P1111 修复公路
#include<iostream>
#include<algorithm>
#define maxm 100010
#define maxn 1010
using namespace std;
struct EDGE
{
    int u,v,tim;
}edge[maxm];
int tot;
void add(int u,int v,int tim)
{
    edge[++tot].v=v;
    edge[tot].tim=tim;
    edge[tot].u=u;
}
bool rule(EDGE a,EDGE b)
{
    return a.tim<b.tim;
}
int fa[maxn];
int fd(int x){return(fa[x]==x?x:fa[x]=fd(fa[x]));}
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        cin>>x>>y>>z;
        add(x,y,z);
    }
    sort(edge+1,edge+tot+1,rule);
    for(int i=1;i<=n;i++)fa[i]=i;
    int ans=0;
    for(int i=1;i<=m;i++)
    {
        int u=edge[i].u,v=edge[i].v;
        if(fd(u)==fd(v))continue;
        ans=edge[i].tim;
        fa[fd(u)]=fd(v);
    }
    int root=fd(1);
    for(int i=2;i<=n;i++)if(fd(i)!=root)return cout<<-1,0;
    cout<<ans;
    return 0;
}

我这个做法没写按秩还是AC了

然后就是我这个无论如何都等到了m条边遍历完

如果是在循环中统计集合个数，==1直接return输出，循环出来-1会更快

2.P1955 [NOI2015] 程序自动分析 - 洛谷

这道题其实特别简单

最开始我以为只需要半离线

把≠先离线（其实就相当于讯问了）

然后＝具有传递性，直接放在同一集合

最后看看离线下来那些≠

在同一集合直接X

但是！！

1≤i,j≤1e9

看到这玩意直接吓哭孩子了

证据：#define maxi 1000000010

其实仔细一想，最多只会用到2n个数，其他的都没意义

（于是我开始尝试在不知道有“离散化”这个东西的情况下，手搓离散化）

（最开始想的是结构体存储对应关系，后来想到要1~tot循环查找2n次）

（时间复杂度直接飙升n^2，直接放弃了）

（看了题解才知道——啥玩意？有专门的算法？叫“离散化”？）

离散化

总得来说离散化有三步走战略：

1.去重（可以用到unique去重函数）排序

3.二分索引（可以用到lower_bound函数）

（摘自追梦_Chen）

见这篇博客

举例：

a：{1,100,10,10000,1000,100}——原数组

t：{1,100,10,10000,1000,100}——复制

t：{1,10,100,100,1000,10000}——排序

t：{1,10,100,1000,1000}——unique//若有不需去重的，有更好做法，还是见那篇博客

去重后不相同元素的个数：就是函数返回值减去集合的初始位置。

a 这里的删除不是真的delete，而是将重复的元素放到容器末尾
b 一定要先对数组进行排序才可以使用unique函数
c unique函数的返回值是去重之后的尾地址

（引自博客）

a：{1,3,2,5,4,5}——lower_bound

具体解释最后一行

a[1]:1//我喜欢从1开始

在t里找到1的下标——1

a[1]=1

a[2]:100

在t里找到100的下标——3

a[2]=3

以此类推

因为要离散化，所以必然先离线

剩下的就最开始说的就行了

进士侯人！！

fa数组和离散化数组这些同时涉及到等号左右两个数的这些数组

大小要开2*n！！！

因为n条（不）等式会最多有2*n个数

Talk is cheap , show me the code

//https://www.luogu.com.cn/problem/P1955
//P1955 [NOI2015] ³ÌÐò×Ô¶¯·ÖÎö
#include<iostream>
#include<algorithm>
#include<cstring>
#define maxn 100010
using namespace std;
struct REQU
{
    int x,y,relation;
}a[maxn];
int cre[2*maxn];//一定别忘了开二倍！！！！因为每条指令两个数字
int tot,u[maxn],v[maxn];//赛博半离线
int fa[2*maxn];
int find(int x){return (fa[x]==x?x:fa[x]=find(fa[x]));}
void marge(int x,int y)
{
    x=find(x);y=find(y);
    if(x==y)return;
    fa[x]=y;
}
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n;
        tot=0;
        memset(a,0,sizeof(a));
        memset(cre,0,sizeof(cre));
        cin>>n;
        for(int i=1;i<=n;i++)cin>>a[i].x>>a[i].y>>a[i].relation;

        //*+*+*+*+*+*+*离散化Discretization*+*+*+*+*+*+*
        for(int i=1;i<=n;i++)cre[i]=a[i].x;
        for(int i=1;i<=n;i++)cre[i+n]=a[i].y;
        sort(cre+1,cre+n+n+1);
        int m=unique(cre+1,cre+n+n+1)-cre-1;
        //其实unique是有返回值的，返回值是去重之后的尾地址，减去头地址就是个数
        for(int i=1;i<=n;i++)a[i].x=lower_bound(cre+1,cre+m+1,a[i].x)-cre;//是m不是n+n
        for(int i=1;i<=n;i++)a[i].y=lower_bound(cre+1,cre+m+1,a[i].y)-cre;
        //lower:大于等于，upper:大于
        //我们这里是找等于
        //*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*

        for(int i=1;i<=m;i++)fa[i]=i;
        for(int i=1;i<=n;i++)
        {
            if(a[i].relation==0)
            {
                u[++tot]=a[i].x;
                v[tot]=a[i].y;
                continue;
            }
           marge(a[i].x,a[i].y);
        }
        bool yes=1;
        for(int i=1;i<=tot;i++)
            if(find(u[i])==find(v[i]))
                yes=0;
        if(yes==1)cout<<"YES\n";
        else cout<<"NO\n";
    }
    return 0;
}

然后补充一点：lower_bound那一行，要的就是把数字替换成下标，所以a[i].xy就是直接等于下标

3.P1197 [JSOI2008] 星球大战 - 洛谷

刚开始看这道题，我的第一反应是：

因为这个需要考虑连边方式了，所以感觉就不像是并查集能做出来的题啊

果然：老师：断边维护联通块数量是困难的

我：离线化处理，从最后删的边一条一条加（时光倒流）

被自己的想法吓了一跳

竟然对了！

我的思路：先离线，然后遍历所有删除的点标vis

然后建图，遇到vis=1时，把这条边先存在vis=1的点（可能两个都是）里

可以开一个vector

然后时光倒流，把当前点所有边所指向的联通块的根节点的父亲设置为这个边

最后，完全正确

Talk is cheap , show me the code.

//https://www.luogu.com.cn/problem/P1197
//P1197 [JSOI2008] ÐÇÇò´óÕ½
#include<iostream>
#include<vector>
#define maxm 200010
#define maxn 400020
using namespace std;
int n,m,k;
int u[maxm],v[maxm];
bool vis[maxn];
int a[maxn];
int fa[maxn];
int ans[maxn];
vector <int> mp[maxn];
int find(int x){return (fa[x]==x?x:fa[x]=find(fa[x]));}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)cin>>u[i]>>v[i];
    cin>>k;
    for(int i=1;i<=k;i++)cin>>a[i];
    for(int i=1;i<=k;i++)vis[a[i]]=1;
    for(int i=0;i<n;i++)fa[i]=i;
    int block=n-k;
    for(int i=1;i<=m;i++)
    {
        int x=u[i],y=v[i];
        if(vis[x]==1)
        {
            mp[x].push_back(y);
        }
        if(vis[y]==1)
        {
            mp[y].push_back(x);
        }
        if(vis[x]==0&&vis[y]==0)
        {
            x=find(x);y=find(y);
            if(x!=y)
            {
                block--;
                fa[y]=x;
            }
        }
    }
    ans[k+1]=block;
    for(int i=k;i>=1;i--)
    {
        int p=a[i];
        vis[p]=0;
        block++;
        for(auto to:mp[p])
        {
            if(vis[to]==1)continue;
            if(find(to)!=find(p))
            {
                block--;
                fa[find(to)]=find(p);
            }
        }
        ans[i]=block;
    }
    for(int i=1;i<=k+1;i++)cout<<ans[i]<<"\n";
    return 0;
}

总结：正难则反

常见类型：时间倒流

带权并查集

额外支持操作：

1.给某个元素所在集合当前时刻所在这个集合的所有元素加一个值

2.查询某个元素的值

暴力/朴素操作：

每个点有一个值tag，代表当前点所在子树内，所有的点都要加上这个值

加一个值的时候，加到这个点所在集合代表元素（根）的tag上

查询一个值时，查询的是从根节点到该节点路径上所有tag和

进行集合合并时，把a指向b时，a要减去b的tag

因为b的tag本来只分给b所在子树

结果先a所在子树也在b所在子树内了

如果不做减法操作，那么b的tag就会分给a所在子树

但其实a所在子树并没有这个tag

有点抽象，举个例子

带权并查集详细图解

三个点123（红色代表实际值，方便观察与理解，黄色代表要记录的tag）

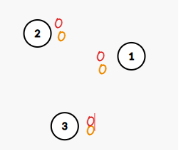
先将2+1，表现为代表元素（2）的tag+1

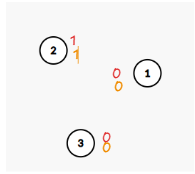
再将2和3合并（2指向3）

所以2的tag要减3的tag，1-0=1

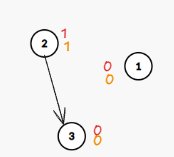
然后再将2+2，表现为代表元素（3）的tag+2

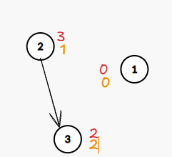
此时，查询2的值，从2的tag一路加到树根3的tag

1+2=3

而查询3的值，就是3的tag本身，为2

再将1的值+1

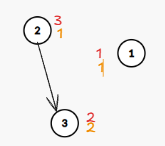
1指向3

此时，1的tag要减去3的tag，1-2=-1

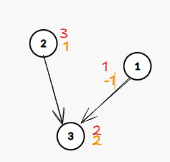
什么？竟然可以出现负数？我一直在加正权值啊

别急，tag并不是-1的值

此时，查询1的值，会发现是1与3的tag相加

-1+2=1

现在好懂多了吧

优化

按秩合并还是那个样，记录size，size小的的fa设置为大的那个

然后大的size+=小的size，这样优化完O(n logn)

但是我们亲爱敬爱的路径压缩就有问题了

因为我们的真实值是要计算一路到达根节点的所有tag的

你这样直接接到根节点上肯定不行

难道你那一路上的所有tag都不要了？

那么，路径压缩，路径压缩

压缩路径不就完事了

把从根节点

（根节点不计入内，因为你接入根节点后，还是要加根节点的tag）

到这个点的路径上的权值加起来

作为这个点新的tag

即新tag=真实值-根节点tag

（根节点tag其实就是根节点真实值）

复杂度也是O（n logn）

P1196 [NOI2002] 银河英雄传说 - 洛谷

这道题其实挺简单的

tag[a]=sz[b]; sz[b]+=sz[a]; fa[a]=b;

这可以算是这道题的状态转移方程吧……

推了有一段时间才推出来的

特点就是需要单独维护一个sz数组，其他的就是带权并查集模板

这是带权并查集的路径压缩

int find(int x)
{
    if(fa[x]==x)return x;//递归·终止条件
    int f=find(fa[x]);//先全部跑一遍，让每一个递归嵌套内的f=根节点
    if(fa[x]!=fa[fa[x]])tag[x]+=tag[fa[x]];//从根节点往下一层一层累加，根节点不加
    return fa[x]=f;//最后直接指向根节点
}

这是查询

int x=tag[find(a)]+tag[a],y=tag[find(b)]+tag[b];

由于这道题，易证根节点tag恒为0

所以孩子节点路径压缩可以多次加根节点的值

压缩后的孩子节点tag-根节点tag=孩子节点tag-0=孩子节点tag=实际值（前面还有几个战舰）

因为在输出答案之前，肯定事先跑过一遍find，压缩完了

所以输出答案时可以不用算，直接用tag就行

（后来补充：不过我后来为了标注模板，我还是压缩时把根节点tag减去了，讯问时把根节点tag加上了）

其余的横看竖看也没看出来啥特别的

毕竟只是绿题

那就这样吧

Talk is cheap, show me the code

//https://www.luogu.com.cn/problem/P1196
//P1196 [NOI2002] ÒøºÓÓ¢ÐÛ´«Ëµ
#include<iostream>
#define maxn 30010
using namespace std;
int fa[maxn],sz[maxn],tag[maxn];
int find(int x)
{
    if(fa[x]==x)return x;//递归·终止条件
    int f=find(fa[x]);//先全部跑一遍，让每一个递归嵌套内的f=根节点
    tag[x]+=tag[fa[x]];//从根节点往下一层一层累加
    return fa[x]=f;//最后直接指向根节点
}
int main()
{
    for(int i=1;i<=30000;i++)fa[i]=i,sz[i]=1;
    int t;
    cin>>t;
    while(t--)
    {
        int a,b;
        char c;
        cin>>c>>a>>b;
        if(c=='M')
        {
            a=find(a);
            b=find(b);
            tag[a]=sz[b];
            sz[b]+=sz[a];
            fa[a]=b;
        }
        else
        {
            if(find(a)!=find(b))cout<<-1<<"\n";
            else
            {
                int x=tag[a],y=tag[b];
                if(x>y)swap(x,y);
                cout<<y-x-1<<"\n";
            }
        }
    }
    return 0;
}

加上根节点tag的标准处理版

//https://www.luogu.com.cn/problem/P1196
//P1196 [NOI2002] ÒøºÓÓ¢ÐÛ´«Ëµ
#include<iostream>
#define maxn 30010
using namespace std;
int fa[maxn],sz[maxn],tag[maxn];
int find(int x)
{
    if(fa[x]==x)return x;//递归·终止条件
    int f=find(fa[x]);//先全部跑一遍，让每一个递归嵌套内的f=根节点
    if(fa[x]!=fa[fa[x]])tag[x]+=tag[fa[x]];//从根节点往下一层一层累加，根节点不加
    return fa[x]=f;//最后直接指向根节点
}
int main()
{
    for(int i=1;i<=30000;i++)fa[i]=i,sz[i]=1;
    int t;
    cin>>t;
    while(t--)
    {
        int a,b;
        char c;
        cin>>c>>a>>b;
        if(c=='M')
        {
            a=find(a);
            b=find(b);
            tag[a]=sz[b];
            sz[b]+=sz[a];
            fa[a]=b;
        }
        else
        {
            if(find(a)!=find(b))cout<<-1<<"\n";
            else
            {
                int x=tag[find(a)]+tag[a],y=tag[find(b)]+tag[b];
                if(x>y)swap(x,y);
                cout<<y-x-1<<"\n";
            }
        }
    }
    return 0;
}

扩展域并查集

这个也非常好理解

就是每个节点都有了多种状态

通常这多种状态不共存

即某个节点一定是某个特殊的状态

所以判断出现错误链接的方法就是同一节点的多个状态在同一个集合内

然后也不是单纯的把a和b放在同一个集合内了

而是把a的某种状态与b的某一种状态放在集合内

这样表示a是这种状态，那么b就是那种状态

所以就好解释为什么一个节点的多种状态不能再同一集合内了

P2024 [NOI2001] 食物链 - 洛谷

这道题可以说是扩展域并查集的标准模板了

我都不想说了

就是先判断是否是谎话

然后真话就合并

假话就ans++

提一下：就是判断是否是假话那里

有个什么性质叫对称性

也就是你任意选择一个状态，他连接上那条边之后

是否会导致出现矛盾

判断出来的情况都是相同的

举个例子

比如说你要描述a与b是同类

于是你可以选择a-1这个状态

他将要和b-1连线

这时候你就要判断a-1与b-2或b-3是否在同一集合内

如果是，那么就是谎话

然后你不仅可以选择a-1这个状态

你选择a-2，a-3都是一样的结果

这就是对称性

（好像并不是所有题都有）

那就直接放代码吧

Talk is cheap, show me the code.

//https://www.luogu.com.cn/problem/P2024
//P2024 [NOI2001] 食物链
#include<iostream>
#define maxn 50010
using namespace std;
int fa[maxn*3];
int find(int x){return(fa[x]==x?x:fa[x]=find(fa[x]));}
void marge(int x,int y)
{
    x=find(x);y=find(y);
    if(x==y)return;
    fa[x]=y;
}
int main()
{
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=3*n;i++)
        fa[i]=i;
    int ans=0;
    while(k--)
    {
        int t,x,y;
        cin>>t>>x>>y;
        if(x>n||y>n)
        {
            ans++;
            continue;
        }
        if(t==1)
        {
            int l=find(x);
            int r1=find(y+n);
            int r2=find(y+2*n);
            if(l==r1||l==r2)
            {
                ans++;
                continue;
            }
            marge(x,y);
            marge(x+n,y+n);
            marge(x+n*2,y+2*n);
        }
        if(t==2)
        {
            if(x==y)
            {
                ans++;
                continue;
            }
            int l=find(x);
            int r1=find(y+2*n);
            int r2=find(y);
            if(l==r1||l==r2)
            {
                ans++;
                continue;
            }
            marge(x,y+n);
            marge(x+n,y+2*n);
            marge(x+2*n,y);
        }
    }
    cout<<ans;
    return 0;
}

额外练习

P1525 [NOIP 2010 提高组] 关押罪犯 - 洛谷

扩展域并查集的板子，比食物链还板子

Talk is cheap, show me the code

//https://www.luogu.com.cn/problem/P1525
//P1525 [NOIP 2010 提高组] 关押罪犯
#include<iostream>
#include<algorithm>
#define maxn 20010
#define maxm 100010
using namespace std;
struct CLS
{
    int left,right,value;
}cls[maxm];
int fa[maxn*2];
int find(int x){return (fa[x]==x?x:fa[x]=find(fa[x]));}
void marge(int x,int y)
{
    x=find(x);
    y=find(y);
    if(x==y)return;
    fa[x]=y;
}
bool rule(CLS a,CLS b)
{
    return a.value>b.value;
}
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=2*n;i++)fa[i]=i;
    for(int i=1;i<=m;i++)cin>>cls[i].left>>cls[i].right>>cls[i].value;
    sort(cls+1,cls+1+m,rule);
    for(int i=1;i<=m;i++)
    {
        int x=cls[i].left,y=cls[i].right,val=cls[i].value;
        if(find(x)==find(y))
            return cout<<val,0;
        marge(x,y+n);
        marge(x+n,y);
    }
    cout<<0;
    return 0;
}

P11811 [PA 2015] 人赢 / Mistrzostwa - 洛谷

（内含一组 hack，如果你只 WA#18）

楼上的各位大佬，讲题思路已经很详细了

因此这篇题解主要的目的是讲几个易错点

那就看看我的死亡回放吧

死亡回放一

30pts

死亡原因：没读题

我没看见有两个问号……所以只输出了集合大小

因此我花费了一次宝贵的测试点下载机会

下载了个样例

那三十分纯粹就是“不可以，总司令！”

然后就能得 30pts

（希望这个神金的死因能让你笑一下）

修改后代码：（非 AC！！）

非AC！

//https://www.luogu.com.cn/problem/P11811
//P11811 [PA 2015] 人赢 / Mistrzostwa
#include<iostream>
#include<queue>
#define maxn 200010
#define maxm 400010
using namespace std;
int out[maxn],vis[maxn];
struct EDGE
{
    int to,next;
}edge[maxm];
int tot=0,head[maxn];
void add(int u,int v)
{
    edge[++tot].to=v;
    edge[tot].next=head[u];
    head[u]=tot;
}
queue <int> q;
int main()
{
    int n,m,d;
    cin>>n>>m>>d;
    for(int i=1;i<=m;i++)
    {
        int a,b;
        cin>>a>>b;
        add(a,b);
        add(b,a);
        out[a]++;
        out[b]++;
    }
    int ans=n;
    for(int i=1;i<=n;i++)
        if(out[i]<d)
        {
            q.push(i);
            vis[i]=1;
        }
    while(!q.empty())
    {
        ans--;
        int p=q.front();
       q.pop();
        for(int i=head[p];i;i=edge[i].next)
        {
            int v=edge[i].to;
            if(vis[v]==1)continue;
            out[v]--;
            if(out[v]<d)
            {
                q.push(v);
                vis[v]=1;
            }
        }
    }
    if(ans==0)cout<<"NIE";
    else
    {
        cout<<ans<<"\n";
        for(int i=1;i<=n;i++)if(vis[i]==0)cout<<i<<" ";
    }
    return 0;
}
/*
4 4 2
1 2
2 3
3 4
4 2

3
2 3 4
*/

死亡回放二

相信大犇们都能看出来我这个代码有大大滴问题

所以只能得 76pts

一个很明显的死因就是：

这张图并不一定联通

所以我不能直接在 n 的基础上进行加减

然后，我才想到本题的主角：并查集

于是我就在建图的时候先连并查集

后来对每一个集合进行类似处理

之后得到的代码就是这个（非 AC！！！！）

非AC！


//https://www.luogu.com.cn/problem/P11811
//P11811 [PA 2015] 人赢 / Mistrzostwa
#include<iostream>
#include<queue>
#define maxn 200010
#define maxm 400010
using namespace std;
int out[maxn],vis[maxn],fa[maxn],num[maxn];
struct EDGE
{
    int to,next;
}edge[maxm];
int tot=0,head[maxn];
void add(int u,int v)
{
    edge[++tot].to=v;
    edge[tot].next=head[u];
    head[u]=tot;
}
int find(int x){return (fa[x]==x?x:fa[x]=find(fa[x]));}
void marge(int x,int y)
{
    x=find(x);
    y=find(y);
    if(x==y)return;
    fa[y]=x;
}
queue <int> q;
int main()
{
    int n,m,d;
    cin>>n>>m>>d;
    for(int i=1;i<=n;i++)fa[i]=i;
    for(int i=1;i<=m;i++)
    {
        int a,b;
        cin>>a>>b;
        marge(a,b);
        add(a,b);
        add(b,a);
        out[a]++;
        out[b]++;
    }
    for(int i=1;i<=n;i++)
    {
        num[find(i)]++;
    }
    for(int i=1;i<=n;i++)
        if(out[i]<d)
        {
            q.push(i);
            vis[i]=1;
        }
    while(!q.empty())
    {
        int p=q.front();
        num[find(p)]--;
       q.pop();
        for(int i=head[p];i;i=edge[i].next)
        {
            int v=edge[i].to;
            if(vis[v]==1)continue;
            out[v]--;
            if(out[v]<d)
            {
                q.push(v);
                vis[v]=1;
            }
        }
    }
    int ans=0,maxnum=0;
    for(int i=1;i<=n;i++)
    {
        if(num[i]>ans)ans=num[i],maxnum=i;
    }
    if(ans==0)return cout<<"NIE",0;
    cout<<ans<<"\n";
    for(int i=1;i<=n;i++)
        if(find(i)==maxnum&&vis[i]==0)
            cout<<i<<" ";
    return 0;
}
/*
4 2 1
4 1
2 3

2
1 4
*/

这其实是一个非常优的骗分解

简直是我见过写过的最优的骗分解

因为它可以骗到 97pts 的高分！！

死亡回放三

可是您是要 AKIOI 的人！

不允许有一分的丢失！

大犇们看我代码也看出来了

我这个代码有个非常严重的问题

就是导出子图不一定联通

hack 在这！！

举个例子：

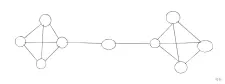
比如这张图 d = 3

那么扫描一遍就会把中间的那个店删掉

之后在扫描，就会发现所有点都“合法”

于是程序就会把剩下并不联通的八个点一起输出了

那通过这个，我们就能看出：

在删边前就维护集合是行不通的

因为断边之后，集合的连通性会发生改变，而你却不自知

又因为断边维护集合是困难的

因此正确答案昭然若揭：

先断边，再跑并查集

（不是这么简单的道理我咋没想到呢）

正解我就不讲了

楼上各位大犇讲得都很详细

那我就直接扔代码了

（AC）

Talk is cheap, show me the code.

//https://www.luogu.com.cn/problem/P11811
//P11811 [PA 2015] ÈËÓ® / Mistrzostwa
#include<iostream>
#include<queue>
#define maxn 200010
#define maxm 400010
using namespace std;
int out[maxn],vis[maxn],fa[maxn],num[maxn];
struct EDGE
{
    int to,next;
}edge[maxm];
int tot=0,head[maxn];
void add(int u,int v)
{
    edge[++tot].to=v;
    edge[tot].next=head[u];
    head[u]=tot;
}
int find(int x){return (fa[x]==x?x:fa[x]=find(fa[x]));}
void marge(int x,int y)
{
    x=find(x);
    y=find(y);
    if(x==y)return;
    fa[y]=x;
}
queue <int> q;
int main()
{
    int n,m,d;
    cin>>n>>m>>d;
    for(int i=1;i<=n;i++)fa[i]=i;
    for(int i=1;i<=m;i++)
    {
        int a,b;
        cin>>a>>b;
        add(a,b);
        add(b,a);
        out[a]++;
        out[b]++;
    }
    for(int i=1;i<=n;i++)
        if(out[i]<d)
        {
            q.push(i);
            vis[i]=1;
        }
    while(!q.empty())
    {
        int p=q.front();
       q.pop();
        for(int i=head[p];i;i=edge[i].next)
        {
            int v=edge[i].to;
            if(vis[v]==1)continue;
            out[v]--;
            if(out[v]<d)
            {
                q.push(v);
                vis[v]=1;
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        if(vis[i]==1)continue;
        for(int j=head[i];j;j=edge[j].next)
        {
            int t=edge[j].to;
            if(vis[t]==1)continue;
            marge(i,t);
        }
    }
    for(int i=1;i<=n;i++)
        if(vis[i]==0)
            num[find(i)]++;
    int ans=0,maxnum=0;
    for(int i=1;i<=n;i++)
    {
        if(num[i]>ans)ans=num[i],maxnum=i;
    }
    if(ans==0)return cout<<"NIE",0;
    cout<<ans<<"\n";
    for(int i=1;i<=n;i++)
        if(find(i)==maxnum&&vis[i]==0)
            cout<<i<<" ";
    return 0;
}
/*
4 2 1
4 1
2 3

2
1 4
*/