关于被巨模拟爆草的感悟与见解（题解）

众所周知，中国赛题看模拟，模拟赛题看山东

SDOI 2015 立体图

继2010年某国杀之后的又一道GIANT模拟。

某国杀已经被吐槽讲过了，那我就来继续吐槽说说立体图。

先看题面

rt。

题目描述

小渊是个聪明的孩子，他经常会给周围的小朋友们讲些自己认为有趣的内容。最近，他准备给小朋友们讲解彩色平行光源照射下的立体图，并请你帮他在平面上画出来。

小渊有一块面积为 \(m \times n\) 的矩形区域，上面有 \(m \times n\) 个边长为 \(1\) 的格子，每个格子上堆了一些同样大小的积木（积木的长宽高都是 \(1\) ）。

为了方便阐述，我们假设这块区域是坐北朝南的，下面我们给出一个例子。

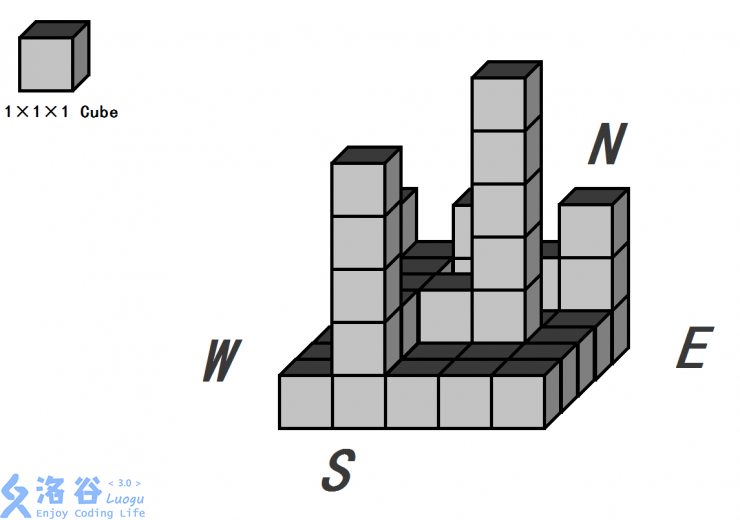
小渊想请你打印出这些格子的立体图。我们定义每个积木为如下格式，并且不会做任何翻转旋转，只会严格以这一种形式摆放（左侧是应该打印出来的图样，右侧为对应每一个位置符号的十进制ASCII，其中ASCII为 \(32\) 的符号为空

在良好的光学环境下，小渊将 \(T\) 束平行光同时照射在这些积木上。这些平行光首先满足一定是红绿蓝三基色之一，其次入射角度满足：与 \(x\) 轴 \(y\) 轴的夹角度数均为 \(45\) 的倍数；且与 \(z\) 轴正方向的夹角或为 \(45\) 度，或为 \(0\) 度，或为 \(315\) 度。

具体来说，我们最多会考虑 \(9\) 个方向的不同平行光，它们的入射方向可以被描述为：

西北方 \(45\) 度仰角 正北方 \(45\) 度仰角 东北方 \(45\) 度仰角
正西方 \(45\) 度仰角 垂直从上的入射光 正东方 \(45\) 度仰角
西南方 \(45\) 度仰角 正南方 \(45\) 度仰角 东南方 \(45\) 度仰角

对于每一个单位积木来说，可以打印出来的三个表面被分为 \(12\) 个小三角形。

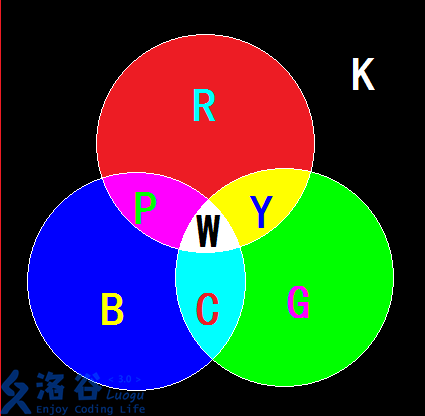
红绿蓝三基色分别用字母R，G，B来表示。而二次叠加后的三种颜色青黄紫，分别用C，Y，P来表示。对于三次叠加后的颜色，也就是白色，用W来表示。

输入格式

第一行有两个正整数 \(m\) 和 \(n\)，表示区域有 \(m\) 行 \(n\) 列。之后 \(m\) 行，依次由远及近描述了每一行的情况。每一行给出 \(n\) 个正整数，表示第 \(i\) 行第 \(j\) 列中有堆放了多少积木。之后 \(3\) 行，每行三个字符，描述了 \(9\) 个对应方向（与地图描述方向相同）的光照颜色。其中每一个字符或者为R，G，B中之一，表示对应的颜色。或者为*，表示没有照射光。这九个方向依次是：

西北方 \(45\) 度仰角 正北方 \(45\) 度仰角 东北方 \(45\) 度仰角
正西方 \(45\) 度仰角 垂直从上的入射光 正东方 \(45\) 度仰角
西南方 \(45\) 度仰角 正南方 \(45\) 度仰角 东南方 \(45\) 度仰角

输出格式

输出给出了打印后的效果。其中要求输出结果不含前导空行，结尾也没有额外空行。输出的第一列不能全是空格，且每一行末尾也没有额外空格。

输入输出样例 #1

输入 #1

2 2
2 1
1 1
R**
***
**G

输出 #1

        +-------+
       /Y\YYYY'/|
      /YY.*'YY/G|
     /.YYYY\Y/G/|
    +-------+G.G|
    |\GGGGG/|\:G|
    |G\GGG/G|G*G|
    |GG\G/GG|G:\|
    |GGGXGGG|G'G+-------+
    |GG/G\GG|/G/G\YYYY'/|
    |G/GGG\G|G/GG.*'YY/G|
    |/GGGGG\|/.GGGG\Y/G/|
    +-------+-------+G.G|
   /Y\GGGG'/G\GGGG'/|\:G|
  /YY.*'GG/GG.*'GG/G|G*G|
 /.YYYY\G/.GGGG\G/G/|G:\|
+-------+-------+G.G|G'G+
|\GGGGG/|\GGGGG/|\:G|/G/
|G\GGG/G|G\GGG/G|G*G|G/
|GG\G/GG|GG\G/GG|G:\|/
|GGGXGGG|GGGXGGG|G'G+
|GG/G\GG|GG/G\GG|/G/
|G/GGG\G|G/GGG\G|G/
|/GGGGG\|/GGGGG\|/
+-------+-------+

输入输出样例 #2

输入 #2

3 4
1 1 2 1
1 2 1 2
2 1 2 1
**B
***
R*G

输出 #2

                            +-------+
                           /W\WWWW'/|
                          /WW.*'WW/C|
                         /.WWWW\W/C/|
                +-------+-------+-------+
               /W\WWWW'/|\YYYYY/W\WWWW'/|
              /WW.*'WW/C|G\YYY/WW.*'WW/C|
             /.WWWW\W/C/|GG\Y/.WWWW\W/C/|
    +-------+-------+-------+-------+C.C|---+
   /W\WWWW'/|\YYYYY/W\WWWW'/|\YYYYY/|\:C|C'/|
  /WW.*'WW/C|G\YYY/WW.*'WW/C|G\YYY/Y|C*C|C/C|
 /.WWWW\W/C/|GG\Y/.WWWW\W/C/|GG\Y/YY|C:\|/C/|
+-------+C.G|GGG+-------+C.G|GGGXYYY|C'C+C.C|
|\YYYYY/|\:G|GG/|\YYYYY/|\:G|GG/G\YY|/C/|\:C|
|Y\YYY/Y|C*G|G/K|Y\YYY/Y|C*G|G/GGG\Y|C/C|C*C|
|YY\Y/YY|C:\|/KK|YY\Y/YY|C:\|/GGGGG\|/C/|C:\|
|YYYXYYY|C'G+---|YYYXYYY|C'G+-------+C.C|C'C+
|YY/Y\YY|/G/G\KK|YY/Y\YY|/G/G\GGGG'/|\:C|/C/
|Y/YYY\Y|G/GG.*'|Y/YYY\Y|G/GG.*'WW/C|C*C|C/
|/YYYYY\|/.YYYY\|/YYYYY\|/.WWWW\W/C/|C:\|/
+-------+-------+-------+-------+C.C|C'C+
|\YYYYY/|\YYYYY/|\YYYYY/|\YYYYY/|\:C|/C/
|Y\YYY/Y|Y\YYY/Y|Y\YYY/Y|Y\YYY/Y|C*C|C/
|YY\Y/YY|YY\Y/YY|YY\Y/YY|YY\Y/YY|C:\|/
|YYYXYYY|YYYXYYY|YYYXYYY|YYYXYYY|C'C+
|YY/Y\YY|YY/Y\YY|YY/Y\YY|YY/Y\YY|/C/
|Y/YYY\Y|Y/YYY\Y|Y/YYY\Y|Y/YYY\Y|C/
|/YYYYY\|/YYYYY\|/YYYYY\|/YYYYY\|/
+-------+-------+-------+-------+

说明/提示

样例 \(2\) ：

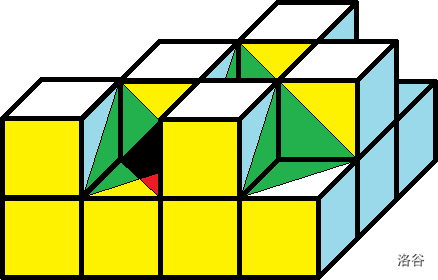
对于 \(15\%\) 的数据，没有入射光。

对于另外 \(40\%\) 的数据，入射光只有一束，且入射方向一定是东南方。

对于 \(100\%\) 的数据，\(1 \le n,m \le 100\)，每一个位置堆放的积木总数不超过 \(100\)，入射光颜色可能是R，G，B中的任何一种颜色，最多可以有 \(9\) 束入射光。

看完了？现在开始解题。

开始被爆草

声明变量

对于以下的若干变量，等到下面详细讲解时大家应该就会明白了。

我们使用二维数组 \(a\) 来存储每一格的立方体数量，二维数组 \(light\) 来存储所给出的 \(3 \times 3\) 光照情况。

设一共需要输出 \(M\) 行，每行 \(N_i\) 个有效字符，所有 \(M\) 行从第一个字符开始的最大公共全空格 串长度为 \(x\)，\(start\) 为为了去除空列，一共所需要将整个图像左移的列数，\(no\) 为是否需要在增加 \(start\) 时退出循环。

\(x\) 是一个六维bool数组，意义分别为：行坐标，列坐标，海拔，面编号，区域编号，光颜色编号。整体意义为坐标是前三个下标的立方体，面编号为第四个下标的第五个下标所编号的区域是否被第六个下标所对应的光照到。\(nx\) 是一个五维bool数组，相对于 \(x\) 少了一维光颜色编号，因为它仅仅存储当前的光是否照到坐标是前三个下标的立方体，面编号为第四个下标的第五个下标所编号的区域（好啰嗦...）。其中，顶部面标号为 \(0\)，东侧面标号为 \(1\)，南侧面标号为 \(2\)；对于每一个面的四个区域，从左边那一个的开始从 \(0\) 开始顺时针标号。如图。

\(b\) 是一个关键参量，用来判断某束光线究竟能否照到立方体的某个区域上。

我们所需要输出的答案为二维字符数组 \(ans\)，其中在对每个立方体进行赋值操作的时候，\(dx\) 为所遍历到的相对于立方体第一行多出的行数，\(dy\) 为相对于最左边那一列多出的列数。

处理输出格式

作为一切的基础，我们首先要考虑如何作出立方体本体。这是第一步，也是最简单的一步，虽然还是很繁琐。。。

对于这个板块，我们需要思考几个问题：

1. \(M\) 等于几？
2. \(N_i\) 如何计算？
3. 如何去除前 \(x\) 列的所有空格 ？（或者说，\(start\) 等于几？）

如果你成功独立地推出了式子，你已经迈出了这一个步骤中关键的一大步。（然后NOIP 2008普及组的极致弱化版立体图你就基本可以拿满分了。如果推不出来就拿它练练手，保证当你看回这道题时就会知道那道题是有多么的眉清目秀了。）

开始推导。

问题1

首先我们可以注意到（如果没注意到就一个个数），每一个立方体正面的总行数为 \(9\)。并且，对于摞在一起的立方体，有一条边是共享的。容易得到，在第 \(i\) 行 \(j\) 列，仅仅对于正面高度来说，行数式子为：

\[M_1=9+((a_{i,j}-1) \times 8) \]

接着，顶部的总行数为 \(4\)（不包括最下面那一行）。

\[M_2=M_1+4 \]

最后，考虑到越靠后（对应的 \(i\) 越小）的立方体在视觉上越高，那么对于侧面，除了最下面一行，斜向高度共有 \(4\) 行，那么立方体每往后靠一行，对应的行数加 \(4\)；对于第 \(m\) 行的立方体，则不用加。

\[M=M_2+((m-i) \times 4) \]

整理，得

\[M=\max(M,13+((a_{i,j}-1) \times 8)+((m-i) \times 4)) \]

只需要整体遍历一遍，即可求出 \(M\)。

至此，问题 \(1\) 解决，输出的时候控制输出 \(M\) 行即可。

（一个防止输出多余空行的小技巧：既然我们使用for(int i=1;i<=M;i++)这样的语句来作为输出答案的最外层循环，那么只需要在开头写一句if(i>1) printf("\n");来使得在第二行及以上才进行开头换行就好了。）

for(int i=1;i<=M;i++){
    if(i>1){
        printf("\n");
    }
}

问题2

我们仍然可以注意到（如果还没注意到就去再数一遍），立方体正面的宽度为 \(9\) 个字符。每往右边一格（对应的 \(j\) 值越大），就会横向增加 \(8\) 个字符长。

\[N_{i1}=9+((j-1) \times 8) \]

其次，侧面除去最左面一列，宽度为 \(4\)。

\[N_{i2}=N_{i1}+4 \]

最后，我们还可以发现，当立方体越靠后时，它所对应在视觉上也是更加靠右的，且同样每靠后一格，偏右 \(4\) 个字符，即

\[N_i=N_{i2}+((m-i) \times 4) \]

整理，得

\[N_i=\max(N_i,13+((j-1) \times 8)+((m-i) \times 4)) \]

...吗？

我们还可以发现，对于从上往下数第 \(10\) 至第 \(13\) 行，结尾有若干个字符是空白的！也就是说，对于每个立方体的最后 \(4\) 行，我们需要特殊处理。

\[N_{i3}= \begin{cases} 13+((j-1) \times 8)+((m-i) \times 4) & (0 \le dx < 9)\\ 13+((j-1) \times 8)+((m-i) \times 4)-(dx-8) & (9 \le dx \le 12) \end{cases} \]

于是，便有

\[N_i=\max(N_i,N_{i3}) \]

所以在我们对 \(ans\) 进行赋值的时候，顺便处理一下每个 \(i\) 所对应的 \(N_i\) 就好了。

至此，问题 \(2\) 解决。

问题3

这个问题其实很好解决，想必大家都已经有个思路了。外层循环列，内层循环行，如果遇到第一个非\0字符，直接将 \(no\) 设置为true，break掉即可，否则每完成一次内层循环，便start++。

bool no=0;
int start=0;
for(int i=1;i<=N[1];i++){
    for(int j=1;j<=M;j++){
        if(ans[j][i]){
            no=1;
            break;
        }
    }
    if(no){
        break;
    }
    start++;
}

至此，问题 \(3\) 解决。

至于为什么要选取 \(N_1\) 作为 \(j\) 循环的大范围？如果 \(N_1\) 没有有效字符，那么它会在解决问题 \(1\) 时被直接忽略掉，不被计算在内，所以不会出现这种情况；如果有有效字符，那么最晚碰到的有效字符一定会在它里面啊！

输出答案时的 \(j\) 循环代码如下：

for(int j=1+start;j<=N[i];j++){
    if(ans[i][j]=='\0'){
        printf(" ");
    }else{
        printf("%c",ans[i][j]);
    }
}

好的，费尽九牛二虎之力，我们终于成功迈出了这一步——处理输出格式。。。

绘制立方体本身

对于这一步的式子，在解决第一步时已经完成了大半——只需要微调一下即可。

我们继续思考：

1. 如何不重不漏地填充每一个立方体？
2. 如何将每一个立方体映射到它应该在的位置？
3. 在打印到需要输出颜色字符的地方时，该怎么计算究竟输出哪种字符呢？

问题1

我们使用 \(i\) 和 \(j\) 循环遍历调用的方式来进行 \(ans\) 的填充。具体来说，我们定义一个 \(put\) 函数，然后对于每一个 \(a_{i,j}\) 循环调用进行更新即可。注意：为了实现遮挡效果，必须采用先后后前，先左后右，先下后上的顺序进行更新。

for(int i=1;i<=m;i++){
    for(int j=1;j<=n;j++){
        for(int k=1;k<=a[i][j];k++){
            put(i,j,k);
        }
    }
}

至此，问题 \(1\) 解决。

问题2

\(put\) 函数的实现应该比较显然了，我再说一下。

对于第 \(x\) 行，第 \(y\) 列从下往上数的第 \(z\) 个立方体，它左上角那个字符的坐标应该是几呢？既然已知 \(ans\) 共 \(M\) 行，那么经过之前的推理，我们可以直接使用公式计算出来它下面究竟有多少行字符，那么它的行坐标 \(startx\) 应该为

\[startx=M-(13+((m-x) \times 4)+((z-1) \times 8))+1 \]

同理，列坐标 \(starty\) 应该为

\[starty=((m-x) \times 4)+((y-1) \times 8)+1 \]

直接循环填充即可。

void put(int x,int y,int z){
    int startx=M-(13+4*(m-x)+8*(z-1))+1;
    int starty=1+4*(m-x)+8*(y-1);
    int dx,dy;
    for(int i=startx;i<=startx+12;i++){
        dx=i-startx;
        if(dx<9){//这里便是之前提到的N_i的更新逻辑了
            N[i]=mx(N[i],starty+12);
        }else{
            N[i]=mx(N[i],starty+12-dx+8);
        }
        for(int j=starty;j<=starty+12;j++){
            dy=j-starty;
            //这里需要使用switch一类的条件判断或者直接使用立方体数组来进行填充，限于篇幅（作者用了292行），不作示例
            //...
        }
}

至此，问题 \(2\) 解决。只需要将立方体每个字符一一实现，就好了。

问题3

每当我们碰到需要输出颜色字符的地方时，就调用 \(mix\) 函数进行计算，再输出返回值即可。

在 \(mix\) 函数中，我们可以先将 \(x\) 数组对应的值赋到 \(r\)，\(g\)，\(b\) 三个bool变量，再进行分讨。

char mix(int x0,int y0,int z0,int face,int part){
    bool r=x[x0][y0][z0][face-1][part-1][0];//这里的-1是因为作者在实现put函数时所给face和part赋的值与x的下标没有匹配上，这里调整一下
    bool g=x[x0][y0][z0][face-1][part-1][1];
    bool b=x[x0][y0][z0][face-1][part-1][2];
    if(r){//如果有红光
        if(g){//如果有绿光
            if(b){//如果有蓝光
                return 'W';//三个都有，直接返回白光
            }else{
                return 'Y';//没有蓝光，但还有绿光，返回黄光
            }
        }else if(b){
            return 'P';//没有绿光，但还有蓝光，返回紫光
        }else{
            return 'R';//连蓝光都没有，返回红光
        }
    }else if(g){//没有红光，如果有绿光
        if(b){//如果有蓝光
            return 'C';//有蓝绿光，返回青光
        }else{
            return 'G';//也没有蓝光，返回绿光
        }
    }else if(b){//也没有绿光，如果有蓝光
        return 'B';//返回蓝光
    }else{//三个光都没有
        return 'K';//返回无光
    }
}

这一部分还是挺简单的...对吧？

计算光线

这道题还是很考验我们的空间想象能力的，像是上下左右中这五个方向应该还很好理解，但是斜向的四个方向就不一定了。

我们使用 \(golight\) 函数来封装它。

在 \(golight\) 函数里，我们需要继续思考几个问题：

1. 使用什么方法，什么顺序进行更新比较简单直接呢？
2. 每一束光所影响的范围是什么？或者说，对于每一个立方体，它对于每束光线的阴影可能会覆盖到哪些其余立方体上？
3. 在什么情况下，立方体会成功地将自己的阴影覆盖到那些对应的立方体上呢？

问题1

有两种主要的方式：一种是遍历每一个立方体，对它进行单独计算；另一种是遍历 \(light\) 数组，如果发现非*字符就进行对应操作。

在这里，我们使用第二种方法。

直接在 \(golight\) 函数中进行大分讨，针对这九种情况分别进行计算即可。

if(light[2][2]!='*'){
    //...
}
if(light[1][2]!='*'){
    //...
}
if(light[2][1]!='*'){
    //...
}
if(light[3][2]!='*'){
    //...
}
if(light[2][3]!='*'){
    //...
}
//...

对于R，G，B三种颜色究竟应该对应什么标号，直接使用 \(numcol\) 函数实现就好了。

int numcol(char c){
    if(c=='R'){
        return 0;
    }else if(c=='G'){
        return 1;
    }else if(c=='B'){
        return 2;
    }else{
        return -10000000;//你要是敢搞什么非法输入，我就RE给你看:(
    }
}

问题 \(1\) 就解决了。

问题2

这个问题其实有 \(9\) 个子问题，分别对应九个方向上的光。

一个细节：对于斜向的影子，为了简化题目，是会遮住所在方向上立方体的一整个顶部的，也就是说，在这些方向上的影子其实会被拉伸为原来的 \(\sqrt2\) 倍。具体如下图。

光（2，2）（垂直光）

显然，这束光线会不重不漏，完美地照到每一个格子最上面的立方体的顶面，所以根本没有立方体会影响到其他坐标上的立方体。

光（1，2）（正北光）

先考虑这束光是因为它所涉及到的也很少，主要就是每个立方体南边的所有立方体的顶部，然后就没什么了。因为它所可能投影到的侧面是每个立方体的北侧面，我们又看不见，管它干嘛。

光（2，1）（正西光）

同理，也只需要考虑正东方每个立方体的顶部，就行了。

光（3，2）（正南光）

这里需要考虑的就稍微多一些了——因为它所会投影到的侧面是南侧面，是会被我们看到的，所以除了对北方的立方体的顶部进行考虑以外，还需要考虑它们的南侧面。

光（2，3）（正东光）

同理，需要考虑的是正西方立方体的顶部和东侧面。

光（1，1）（西北光）

对于斜向的光，我们需要考虑的就更多了。尽管这个光线要考虑的相对来说也很少罢了

首先我们可以轻而易举地想象到它所影响到的立方体肯定包括正东南方的所有立方体的顶部；再者，我们还可以想象到，对于每一个正东南方的被遮住的立方体，它北边第一个立方体的顶部区域 \(0\) 和 \(3\) 和西边第一个立方体的顶部区域 \(1\) 和 \(2\) 也是会被遮住的。如果想象不到，看这个图。

然后就没什么别的要考虑的了。

光（3，1）（西南光）

从这里开始，事情变得复杂了起来...

首先很显然，正东北方的立方体顶部是会被遮住的；其次，根据刚刚的经验，这正东北方的立方体的西方第一个和南方第一个立方体的顶部是会分别被遮住区域 \(2\) 和 \(3\)，\(0\) 和 \(1\) 的。

从这里开始，大家应该有个想象的模板了吧qwq

其次，我们再来思考，对于正东北方的立方体，除了会被影响到顶面以外，南侧面会不会也被遮住呢？

如图，区域 \(0\) 和 \(3\) 被遮挡了。

还有，这个正东北方的立方体的西方第一个立方体的南侧面也是会被遮住的！！！

至于为什么总是不删之前图片的注解？还不是怕你忘了

光（1，3）（东北光）

同上，正西南方立方体的顶部和东侧面区域 \(2\) 和 \(3\) 会被遮挡住，它们北方一格和东方一格的立方体也会被遮住顶部，区域分别是 \(2\) 和 \(3\)，\(0\) 和 \(1\)，且正北方一格的那个立方体会被遮住东侧面。

光（3，3）（东南光）

明明作为特殊性质出现，却是最难实现的一个

与上面类似，只是又多了一倍的思考量和代码量。

正西北方立方体：顶面，南侧面区域 \(2\) 和 \(3\)，东侧面区域 \(0\) 和 \(3\)；

它的东边一格立方体：顶面区域 \(0\) 和 \(3\)，南侧面；

它的南边一格立方体：顶面区域 \(1\) 和 \(2\)，东侧面。

算了还是放图吧。

东一格示例：

南一格示例：

呜呼...问题 \(2\) 终于完成了...

然而更精彩的还在后面捏QAQ

问题3

emm...没错，仍然是 \(9\) 个子问题。

光（2，2）（垂直光）

显然，用不着讨论
因为它的影子在正下方待着，所以根本不会影响到任意一个其它的立方体！

直接赋值就好了。

for(int i=1;i<=m;i++){
    for(int j=1;j<=n;j++){
        for(int k=0;k<4;k++){
            x[i][j][a[i][j]][0][k][numcol(light[2][2])]=1;
        }
    }
}

光（1，2）（正北光）

看图。

容易发现：

• 如果侧面被挡住，那么必然满足两个方块之间的高度差（特指投影的柱子高度减被投影的柱子的高度）大于等于它们之间的横向距离 \(-1\)。
• 如果顶面被挡住，那么必然满足两个方块之间的高度差（意义同上）大于等于它们之间的横向距离。

若我们设 \(b=(k-j)-(a_{i,j}-a_{i,k})\)（其中 \(k\) 代表从 \(j+1\) 开始向下枚举的所有正南方向的立方体的 \(j\) 坐标），那么就有

• 如果 \(b>1\)，那么侧面就不会被挡住。（因为这意味着【高度差】与【距离】之间的差是小于 \(-1\) 的）
• 如果 \(b>0\)，那么顶面就不会被挡住。（原因同上）

再来补充说明一下 \(nx\) 的用途：一开始我们默认设其全能照到，然后我们就可以发现：一旦这束光被某个立方体遮住了，它就一定不能再被这束光照到了吧！所以，更新 \(nx\) 的时候，我们使用逻辑与 \(\&\) 来进行更新。

然后，对于立方体，即使它这束光可能接收不到了，但这并不意味着其它的光也会接收不到！但是，如果被它照到了，那就一定是被照到了对吧！（废话）所以，赋值到 \(x\) 上的的时候，我们使用逻辑或 \(|\)。

if(light[2][1]!='*'){
    int b;
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            for(int l=0;l<4;l++){
                nx[i][j][a[i][j]][0][l]=1;
            }
        }
    }
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            for(int k=j+1;k<=n;k++){
                b=k-j-(a[i][j]-a[i][k]);
                for(int l=0;l<4;l++){
                    nx[i][k][a[i][k]][0][l]&=(b>0);
                }
            }
        }
    }
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            for(int k=0;k<4;k++){
                x[i][j][a[i][j]][0][k][numcol(light[2][1])]|=nx[i][j][a[i][j]][0][k];
                nx[i][j][a[i][j]][0][k]=0;
            }
        }
    }
}

光（2，1）（正西光）

其实和正北光类似，就是 \(b\) 的计算公式稍稍变化了，相信应该已经很容易推导了。

光（3，2）（正南光）

同上

这里稍有不同：侧面的更新逻辑被包含在内了。

if(light[3][2]!='*'){
    int b;
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            for(int h=a[i][j];h>=1;h--){
                for(int l=0;l<4;l++){
                    nx[i][j][h][0][l]=1;
                    nx[i][j][h][2][l]=1;
                }
            }
        }
    }
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            for(int k=i-1;k>=1;k--){
                for(int h=a[k][j];h>=1;h--){
                    b=i-k-(a[i][j]-h);
                    for(int l=0;l<4;l++){
                        nx[k][j][h][0][l]&=(b>0);
                        nx[k][j][h][2][l]&=(b>1);
                    }
                }
            }
        }
    }
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            for(int k=1;k<=a[i][j];k++){
                for(int l=0;l<4;l++){
                    x[i][j][k][0][l][numcol(light[3][2])]|=nx[i][j][k][0][l];
                    x[i][j][k][2][l][numcol(light[3][2])]|=nx[i][j][k][2][l];
                    nx[i][j][k][0][l]=0;
                    nx[i][j][k][2][l]=0;
                }
            }
        }
    }
}

光（2，3）（正东光）

同上

光（1，1）（西北光）

确实也是更复杂了，不过只要你完全理解了上面的思路，下面其实可以做到手到拈来！

注意：一定，一定要把投影范围考虑全面啊啊啊！

if(light[1][1]!='*'){
    int b;
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            for(int l=0;l<4;l++){
                nx[i][j][a[i][j]][0][l]=1;
            }
        }
    }
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            int i1=i,j1=j;
            if(i==m){//边界，前人血的教训
                b=1-(a[i][j]-a[i][j+1]);
                nx[i][j+1][a[i][j+1]][0][0]&=(b>0);//更新顶面。使用的还是b>0，挺熟悉的吧
                nx[i][j+1][a[i][j+1]][0][3]&=(b>0);
            }
            if(j==n){
                b=1-(a[i][j]-a[i+1][j]);
                nx[i+1][j][a[i+1][j]][0][1]&=(b>0);
                nx[i+1][j][a[i+1][j]][0][2]&=(b>0);
            }
            while(i1<=m&&j1<=n){
                i1++;//往东南方向走
                j1++;
                b=j1-j-(a[i][j]-a[i1][j1]);
                for(int l=0;l<4;l++){
                    nx[i1][j1][a[i1][j1]][0][l]&=(b>0);
                }
                i1--;
                b=j1-j-(a[i][j]-a[i1][j1]);
                nx[i1][j1][a[i1][j1]][0][0]&=(b>0);
                nx[i1][j1][a[i1][j1]][0][3]&=(b>0);
                i1++;
                j1--;
                b=i1-i-(a[i][j]-a[i1][j1]);
                nx[i1][j1][a[i1][j1]][0][1]&=(b>0);
                nx[i1][j1][a[i1][j1]][0][2]&=(b>0);
                j1++;
            }
        }
    }
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            for(int l=0;l<4;l++){
                x[i][j][a[i][j]][0][l][numcol(light[1][1])]|=nx[i][j][a[i][j]][0][l];
                nx[i][j][a[i][j]][0][l]=0;
            }
        }
    }
}

光（3，1）（西南光）

同上。这里开始需要考虑侧面。

if(light[3][1]!='*'){
    int b;
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            for(int h=a[i][j];h>=1;h--){
                for(int l=0;l<4;l++){
                    nx[i][j][h][0][l]=1;
                    nx[i][j][h][2][l]=1;
                }
            }
        }
    }
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            int i1=i,j1=j;
            if(i==1){
                b=1-(a[i][j]-a[i][j+1]);
                nx[i][j+1][a[i][j+1]][0][0]&=(b>0);
                nx[i][j+1][a[i][j+1]][0][1]&=(b>0);
            }
            if(j==n){
                b=1-(a[i][j]-a[i-1][j]);
                nx[i-1][j][a[i-1][j]][0][2]&=(b>0);
                nx[i-1][j][a[i-1][j]][0][3]&=(b>0);
            }
            while(i1>=1&&j1<=n){
                i1--;//往东北遍历
                j1++;
                for(int h=a[i1][j1];h>=1;h--){
                    b=j1-j-(a[i][j]-h);
                    for(int l=0;l<4;l++){
                        nx[i1][j1][h][0][l]&=(b>0);
                    }
                    nx[i1][j1][h][2][0]&=(b>1);//更新侧面，使用b>1，也挺熟悉的对吧
                    nx[i1][j1][h][2][3]&=(b>1);
                    nx[i1][j1][h][2][1]&=(b>0);
                    nx[i1][j1][h][2][2]&=(b>0);
                }
                j1--;
                for(int h=a[i1][j1];h>=1;h--){
                    b=i-i1-(a[i][j]-h);
                    for(int l=0;l<4;l++){
                        nx[i1][j1][h][2][l]&=(b>1);
                    }
                }
                b=i-i1-(a[i][j]-a[i1][j1]);
                nx[i1][j1][a[i1][j1]][0][2]&=(b>0);
                nx[i1][j1][a[i1][j1]][0][3]&=(b>0);
                j1++;
                i1++;
                b=j1-j-(a[i][j]-a[i1][j1]);
                nx[i1][j1][a[i1][j1]][0][0]&=(b>0);
                nx[i1][j1][a[i1][j1]][0][1]&=(b>0);
                i1--;
            }
        }
    }
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            for(int h=a[i][j];h>=1;h--){
                for(int l=0;l<4;l++){
                    x[i][j][h][0][l][numcol(light[3][1])]|=nx[i][j][h][0][l];
                    x[i][j][h][2][l][numcol(light[3][1])]|=nx[i][j][h][2][l];
                    nx[i][j][h][0][l]=0;
                    nx[i][j][h][2][l]=0;
                }
            }
        }
    }
}

光（1，3）（东北光）

同上，几乎一样。

光（3，3）（东南光）

明明就是作为特殊性质出现的，却还是最难实现的一个
这里就交给读者了——要知道，这里几乎就是精准两倍的代码量，复制粘贴一遍西南光或东北光的代码就差不多了（反正作者是这么干的），之后只需要一些微调。

华丽结尾

return 0;

终于解完啦~说说后话吧

其实本题计算量最大的也就只有处理输出格式那一部分，剩下的重在思考，在脑中构建出模型。大家也看到代码了，后面的“最复杂”的计算光线的那部分涉及到的算式只有 \(b\) 的计算，然而这也基本上就是个公式，处理每个光线时微调一下，这道题就做完了。

这道题不愧是山东省选啊……大体思路很好想，但是细节多到爆炸……本人曾因为忘记在某个不起眼的角落进行 \(b\) 的更新，导致了长达三天对神秘 WA 掉的两点的玄学调试……QAQ

没想到第一次写的随笔居然这么长…还望支持一下吧 qwq（如有疏漏，欢迎指正）

（注：题面描述部分图片摘自网友提供。如有侵权，即刻删除）