二、数据结构
二、数据结构
我总感觉学习算法之前要先学数据结构。但是从一些资料或者书籍看来,它们在目录上的顺序貌似和我感觉的相反。
但是我将继续坚持我的观点。先学 数据结构,再学 算法。
2.1 为什么要学数据结构?
工作中,有一次小菜需要开发一个客服电话系统,他们项目经理安排小菜完成客户排队模块的代码工作。
小菜觉得这个很容易,用数据库设计了一张客户排队衰,并且用 一个自动递增的 整型数字作为客户的编号。只要来一个客户,就给这张表的末尾插入一条数据。等客 服系统一有空闲,就从这张表中取出最小编号的客户提交,并且删除这条记录。花了 两天时间,他完成开发井测试通过后,得意地提交了代码。谁知他们的项目经理,看 完代码后,跑到他的桌前,拍着桌子对他说..你数据结构怎么学的?这种实时的排队模块,用什么数据库呀,在内存中完成不就行了吗。赶快改,今天一定要完成,明天一早交给我。"
小菜吓得一身冷汗,这脸丢得有些大了,自己试用期都投结束,别因此失去工 作。于是他当天加班加点,忙到晚上十一 点,用数组变量重新实现了这个功能,因为 考虑到怕敬组不够大而溢出,于是他设计 100 作为数组的长度。
回到家中,他害怕这个代码有问题,于是就和他的表哥大鸟说起了这个事。
大鸟听后对小菜:“你数据结构怎么学的? 这种实时的排队系统,通常用数据结构中的"队列结构n 是 比较好的,用数组虽然也可以,但是又要考虑溢出,又要考虑新增和删除后的数据移 动,总的说来很不方便。这样.......这样...就可以了。”
小菜在大鸟的帮助下,忙到凌晨 3 点,重新用队列结构又写了一遍代码,上班时 用 U 盘拷回公司,终于算是过了项目经理这一关。
之后,小菜开始重视 数据结构,找回大学的课本重新学习。
2.2 数据结构的起源
早期人们都把计算机理解为数值计算工具,就是感觉计算机当然是用来计算的, 所以计算机解决问题,应该是先从具体间题中抽象出一个适当的数据模型,设计出一个解此数据模型的算法,然后再编写程序,得到一个实际的软件 。
可现实中,我们更多的不是解决数值计算的问题,而是需要一些更科学有效的手段(比如表、树和图等数据结构)的帮助,才能更好地处理问题 。 所以 数据结构是一门研究非数值计算的程序设计问题中的操作对象,以及他们之间的关系和操作等相关问题的学科。
程序设计 = 数据结构 + 算法
2.3 数据结构的基本概念和术语
2.3.1 什么是数据?
数据:是描述客观事物的符号,是计算机中可以操作的对象,是能被计算机识别,并输入给计算机处理的符号集合。
数据不仅仅包括整型、实型等数值类型,还包括字符及声音、图像、视频等非数值类型 。
比如我们现在常用的搜索引擎,一般会有网页、MP3、图片、视频等分类。MP3 就是声音数据,图片当然是图像数据,视频就不用说了,而网页其实指的就是全部数据的搜索,包括最重要的数字和字符等文字数据。
也就是说,我们这里说的数据,其实就是符号,而且这些符号必须具备两个前提:
- 可以输入到计算机中。
- 能被计算机程序处理。
2.3.2 数据元素
数据元素:是组成数据的、有一定意义的基本单位,在计算机中通常作为整体处理。也被称为记录。
在计算机中,数据元素并不是孤立、杂乱无序的,而是具有内在联系的数据集
合。数据元素之间存在的 一种或多种特定关系,也就是数据的组织形式。
为编写出一个“好”的程序,必须分析待处理对象的特性及各处理对象之间存在的关系。这也是研究数据结构的意义所在
2.3.3 数据项
数据项:一个数据元素可以自若干个数据项组成。数据项是数据不可分割的最小单位。
2.3.4 数据对象
数据对象:是性质相同的数据元素的集合,是数据的子集。
2.3.4 数据结构
数据结构:是相互之间存在-种或多种特定关系的数据元素的集舍。
2.3.5 数据项,数据元素与数据对象之间的关系
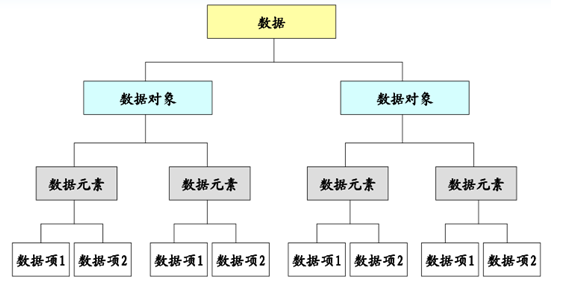
2.4 逻辑结构与物理结构
2.4.1 逻辑结构
逻辑结构:是指数据对象中数据元素之间的相互关系。其实这也是我们今后最需要关注的问题。 逻辑结构分为以下四种:
1. 集合结构
集合结构:集合结构中的数据元素除了 同属于一个集合外,宫们之间没有其他关系。各个数据元素是"平等'的,官们的共同属性是"同属于一个集合"。数据结构中的集合关系就类似于数学中的集合。(如下图)
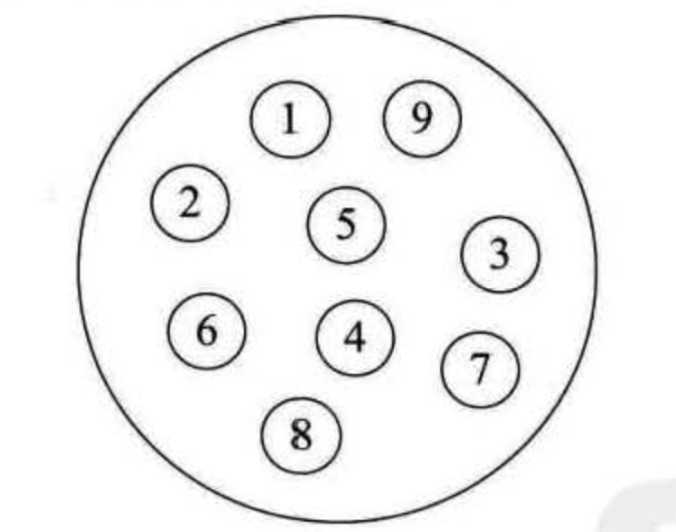
2. 线性结构
线性结构:统性结构中的数据元素之间是一对一的关系。(如下图)
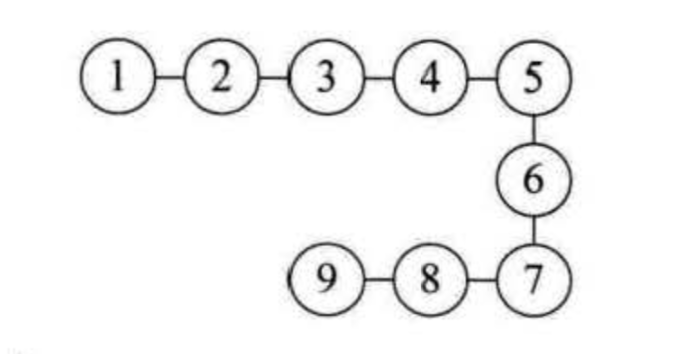
3. 树形结构
树形结构:树形结构中的数据元素之间存在一种一对多的层次关系。(如下图)
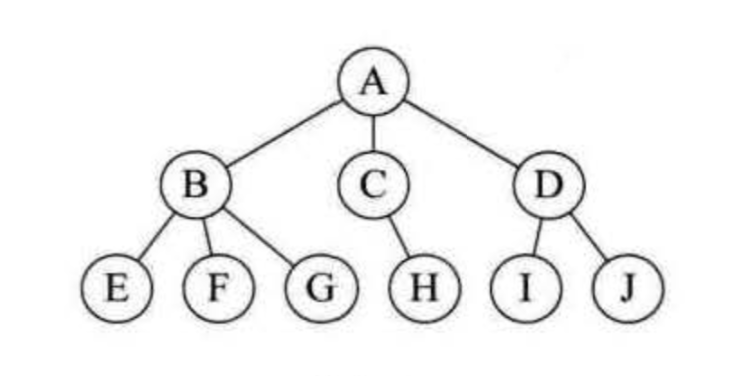
4. 图形结构
图形结构:图形结构的数据元素是多对多的关系。(如下图)
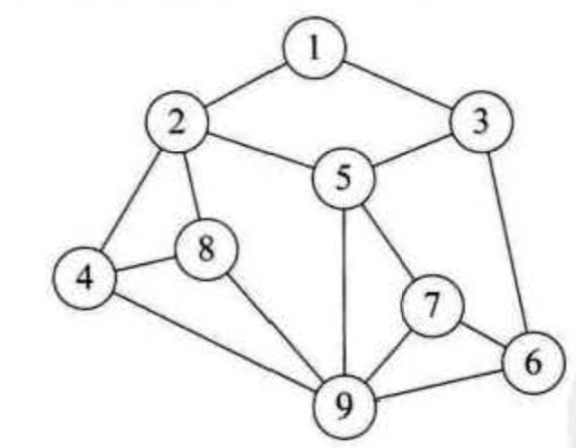
2.4.2 物理结构
物理结构:是指数据的逻辑结构在计算机中的存储形式。
数据元素的存储结构形式有两种:顺序存储和链式存储。
1. 顺序存储结构
顺序存储结构:是把数据元素存放在地址连续的存储单元里,其数据间的逻辑关系和物理关系是一致的。(如下图)

2. 链式存储结构
链式存储结构:是把数据元素存放在任意的存储单元里,这组存储单元可以是连续的,也可以是不连续的。(如下图)
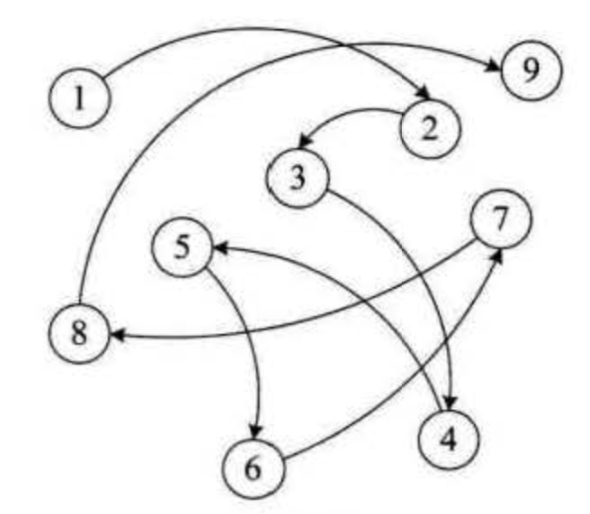
2.5 抽象数据类型
2.5.1 数据类型
(忽略)
2.5.2 抽象数据类型 (Abstract Data Type 简称ADT)
抽象 是指抽取出事物具有的普遍性的本质。它是抽出问题的特征而忽略非本质的细节,是对具体事物的一个概括。抽象是一种思考问题的方式,它隐藏了繁杂的细节,只保留实现目标所必需的信息。
抽象数据类型: 是指一个数学模型及定义在该模型上的一组操作。
描述抽象数据类型的标准格式:
ADT 抽象数据类型名
Data
数据元素之间逗得关系的定义Operation
操作 1
初始条件
操作结来描述
操作 2
操作 n
ENDADT
2.5.3 为什么有了数据类型,还要有抽象数据类型呢?
各个计算机,不管是大型机、小型机、PC、平板电脑、PDA, 甚至智能手机都拥有“整数”类型,也需要整数间的运算,那么整型其实就是一个抽象数据类型,尽管它在上面提到的这些在不同计算机中实现方法上可能不一样,但由于其定义的数学特性相同,在计算机编程者看来,它们都是相同的。因此,“抽象”的意义在于数据类型的数学抽象特性。
而且,抽象数据类型不仅仅指那些已经定义并实现的数据类型,还可以是计算机编程者在设计软件程序时自己定义的数据类型,比如我们编写关于计算机绘图或者地图类的软件系统,经常都会用到坐标。也就是说,总是有成对出现的x和y,在3D 系统中还有z出现,既然这三个整型数字是始终在一起出现,我们就定义一个叫point 的抽象数据类型,它有x、y、z三个整型变量,这样我们很方便地操作一个point数据变量就能知道这一点的坐标了。
抽象数据类型(ADT)的定义和实现通常是分开的。定义只包含数据逻辑结构的定义和所允许的一组操作;使用者通过这些定义了的操作对ADT进行操作;另一方面,实现者根据这些定义来完成 ADT 的各种具体实现方式。
举个线性表的 ADT 例子:
ADT 线性表(List)
Data
线性表的数据对象集合为{a1,a2,......,an},每个元素的类型均为DataType。其中,除第一个元素a1外,每一个元素有且只有一个直接前驱元素,除了最后一个元素an外,每一个元素有且只有一个后继元素。数据元素之间的关系是一对一的关系。
Operation
InitList (*L) : 初始化操作,建立一个空的线性表L。
ListEmpty(L): 若线性表为空,返回true,否则返回false。
ClearList(*L):将线性表清空。
GetElem(L, i, *e):将线性表L中的第i个位置元素值返回给e。
LocateElem(L, e):在线性表L中查找与给定值e相等的元素,如果查找成功,返回该元素在表中序号表示成功;否则,返回0表示失败。
ListInsert(*L, i, e):在线性表L中的第i个位置插入新元素e。
ListDelete(*L, i, *e):删除线性表L中第i个位置元素,并用e返回其值。
ListLength(L):返回线性表L的元素个数。
endADT



 浙公网安备 33010602011771号
浙公网安备 33010602011771号