数据结构--循环队列

实现队列的方法很多，比如动态数组、链表，今天主要介绍循环队列

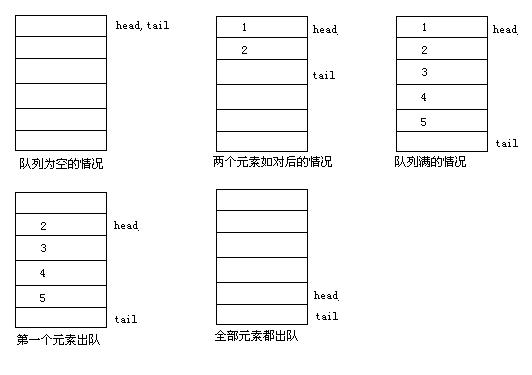
首先说用静态数组实现简单队列。

很显然，当队列满后，即便全部元素都出队，队列还是满的状态。这种情况就叫做“假溢出”，即数组中明明有可用空间，但却无法使用。

这是由定长数组的特性决定的。但我们可用改变一下思路，当队尾指针指向数组最后一个位置时，如果再有数据入队，并且队头指针没有指向数组的第一个元素，那么就让队为指针绕回到数组头部。这样就形成了一个逻辑上的环。

这样，只要队列中实际的元素数量小于数组长度减一，就可以继续入队了。

其实这是一个非常简单的数据结构，难点就是判断队空、对满，以及计算队列长度。

 1const int MAX_QUEUE_SIZE = 5;
 2template<typename T>
 3class cyc_queue
 4{
 5public:
 6    cyc_queue()
 7        :m_nHead(0),
 8        m_nTail(0)
 9    {}


    //如对操作， 将数据追加到队列头部，并改变队首指针，如队成功，则返回true
    bool in_queue(const T & data)
    {
        if(full())
        //队列满
        {
            return false;
        }

        m_array[m_nTail] = data;
        m_nTail = (m_nTail + 1) % MAX_QUEUE_SIZE;
    }

    //出队操作，将队首数据复制并返回，改变队首指针
    T out_queue()
    {
        if(empty())
        {
            throw("队列已空");
        }
        
        T temp = m_array[m_nHead];
        m_nHead = (m_nHead + 1) % MAX_QUEUE_SIZE;
        return temp;
    }

    bool empty()
    {

        return m_nTail == m_nHead;
    }

    bool full()
    {
        return (m_nTail + 1) % MAX_QUEUE_SIZE == m_nHead;
    }

    size_t size()
    {
        return (m_nTail - m_nHead + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE;
    }
private:
    T m_array[MAX_QUEUE_SIZE];
    int m_nHead;
    int m_nTail;
};