算法:leetcode_112_路径总和 - 指南
目录
0. 前言
这是一道面试高频题目, 也是一道回溯模板题,
先贴出力扣链接:
这道题和另一道回溯模板题非常像, 但是更容易错误点。
129. 求根节点到叶节点数字之和 - 力扣(LeetCode)
适合一起做了, 锻炼递归思想,相关笔记可以看看我的另一篇分享博客:算法:leetcode_129_求根节点到叶节点数字之和-CSDN博客
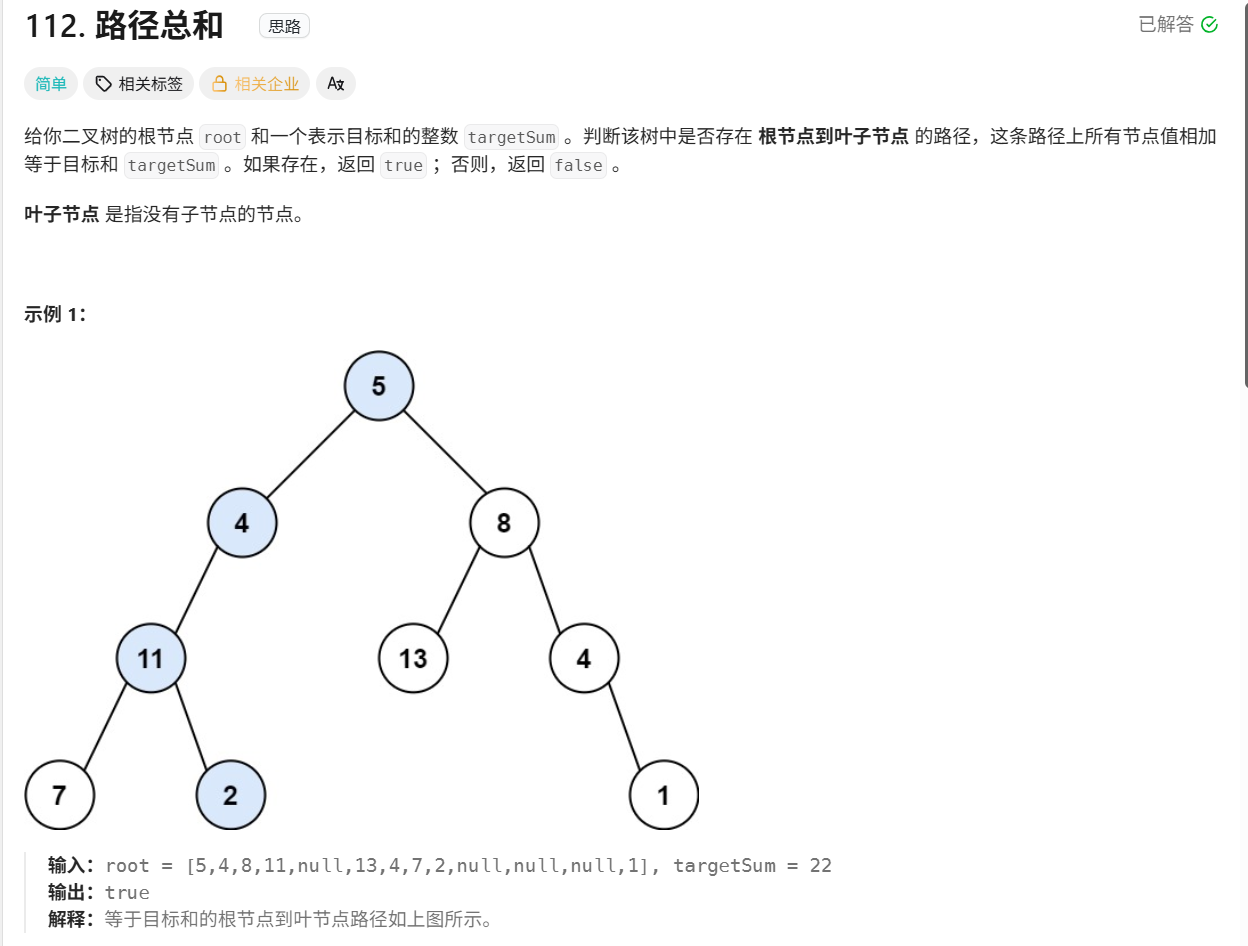
1. 题目介绍
注意:
- 节点数可以为0
- 节点值也可以为负

2. 思路模拟
一起跟着我的思路来吧:
我们刚开始的积分path是0
【为什么变量名字叫path->因为这是访问整条路径的全局变量, 关乎是否能结束游戏,
其他类似的回溯的题目, path通常是作为字符串,链表结构,作为统一就叫path吧。当然变量名字无所谓, 叫sum也行】
每访问完一个节点, 积分加上对应节点的值val :
path += root.val;我们的积分要达到题目给定的22才能够通关, 同时我们已经尽力了: 到达了最深处【叶子节点】:
积分够了 但是还在路中央是不可以的嗷,必须到底!
if(path == target && root.left == null && root.right == null){
return true;
}这个节点访问完了, 但是游戏没结束, 把接下来的任务交给孩子们吧:
left和right代表从这个子节点进去, 最终是否能够完成任务, 不一定就是它本人完成了任务, 大概率是它孙子的孙子的孙子的孙子........... 最底层的叶子节点是否顺利完成了任务。
简洁来说, 以这个子节点为根节点重新开始游戏, 是否能成功。
boolean left = dfs(root.left);
boolean right = dfs(root.right);我已经燃尽了, 准备把任务的结果汇报给上一级:
现在任务是否完成, 取决于孩子, 两个孩子其中有一个完成了任务也算我们胜利!
再提交任务之前, 先把当前已经有的积分给扣除(积分只留给有希望胜利的人), 已经遍历过的节点拿着也没用:
// 两个孩子都处理完了, 自己的任务也完成了, 返回上一层之前先交出它的值
path -= root.val;
// 两个孩子 有一个孩子顺利结束战斗 都算成功
return left || right;当踩空了怎么办, 遇到了空节点, 直接返回!
判空只有两个地方能遇到,
- 访问这整棵树的根节点的时候, 根节点为空, 直接游戏失败;
- 访问完了叶子节点之后, 同时此时拥有的积分path不等于目标值targetSum, 还要遍历叶子节点的左右两个子节点, 但是两孩子都为空, 此时刚dfs进去, 游戏还没开始就结束了。
// 当节点为空 直接返回false
if(root == null) return false;3. 代码
附上详细注释版:
Java:
public class Leetcode_112 {
// 全局 路径变量
public static int path;
// 目标target, 懒得传参, 也整全局
public static int target;
public static boolean hasPathSum(TreeNode root, int targetSum) {
// 赋初值
path = 0;
target = targetSum;
return dfs(root);
}
public static boolean dfs(TreeNode root){
// 当节点为空 直接返回false
if(root == null) return false;
// 先加上当前正在访问节点的值
path += root.val;
// 如果正好path已经等于了目标值 同时它还得是[叶子节点] return true
if(path == target && root.left == null && root.right == null){
return true;
}
// 这个节点遍历完了 但是游戏还没结束
// 遍历左孩子节点和右孩子节点
boolean left = dfs(root.left);
boolean right = dfs(root.right);
// 两个孩子都处理完了, 自己的任务也完成了, 返回上一层之前先交出它的值
path -= root.val;
// 两个孩子 有一个孩子顺利结束战斗 都算成功
return left || right;
}
}简洁版代码:
递归思路熟悉之后, 可以将整体代码简洁为如下:
换个思路, 从结果值开始减:
// 简洁版, 换个思路, 从结果值开始减
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) {
return false;
}
// 如果当前节点为叶子节点
if (root.left == null && root.right == null) {
// 判断是否为目标值
return targetSum == root.val;
}
// 当前节点没有顺利完成任务 那么把任务是否胜利的决定权交给左右两个孩子, 减去当前节点的值, 为孩子完成任务所需的目标值
return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
}C++:
class Solution {
public:
// 全局 路径变量
static int path;
// 目标target, 懒得传参, 也整全局
static int target;
bool hasPathSum(TreeNode* root, int targetSum) {
// 赋初值
path = 0;
target = targetSum;
return dfs(root);
}
private:
bool dfs(TreeNode* root) {
// 当节点为空 直接返回false
if (root == nullptr) return false;
// 先加上当前正在访问节点的值
path += root->val;
// 如果正好path已经等于了目标值 同时它还得是[叶子节点] return true
if (path == target && root->left == nullptr && root->right == nullptr) {
return true;
}
// 这个节点遍历完了 但是游戏还没结束
// 遍历左孩子节点和右孩子节点
bool left = dfs(root->left);
bool right = dfs(root->right);
// 两个孩子都处理完了, 自己的任务也完成了, 返回上一层之前先交出它的值
path -= root->val;
// 两个孩子 有一个孩子顺利结束战斗 都算成功
return left || right;
}
};
// 静态成员定义
int Solution::path = 0;
int Solution::target = 0;JS:
// 全局 路径变量
let path;
// 目标target, 懒得传参, 也整全局
let target;
var hasPathSum = function(root, targetSum) {
// 赋初值
path = 0;
target = targetSum;
return dfs(root);
};
function dfs(root) {
// 当节点为空 直接返回false
if (root === null) return false;
// 先加上当前正在访问节点的值
path += root.val;
// 如果正好path已经等于了目标值 同时它还得是[叶子节点] return true
if (path === target && root.left === null && root.right === null) {
return true;
}
// 这个节点遍历完了 但是游戏还没结束
// 遍历左孩子节点和右孩子节点
const left = dfs(root.left);
const right = dfs(root.right);
// 两个孩子都处理完了, 自己的任务也完成了, 返回上一层之前先交出它的值
path -= root.val;
// 两个孩子 有一个孩子顺利结束战斗 都算成功
return left || right;
}4. 更新预告:
本题做了之后, 可以继续做113. 路径总和 II作为进阶, 让你进一步熟练dfs。
下一步我就会更新113. 路径总和 II, 同样用简单清晰的思路分享给大家。
觉得我的屎山代码能提供帮助的话, 点赞收藏么么哒。
期待下一篇更新的话,可以点点关注mua!, 及时让宝宝们看到。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号