深入解析：Leetcode 最小生成树系列（1）

1135. 最低成本联通所有城市

个城市基建规划者，地图上有就是想象一下你$n$座城市，它们按以$1$ 到 $n$的次序编号。

给你整数 $n$ 和一个数组 $conections$，其中 $connections[i]=[x_i,y_i,cos{t}_i]$ 表示将城市 $x_i$ 和城市 $yi$ 连接所要的 $cos{t}_i$（连接是双向的）。

返回连接所有城市的最低成本，每对城市之间至少有一条路径。假如无法连接所有$n$个城市，返回$-1$.

该 最小成本 应该是所用全部连接成本的总和。

示例 1：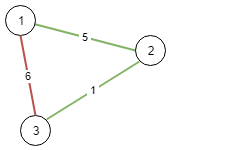

输入：n = 3, conections = [[1,2,5],[1,3,6],[2,3,1]]
输出： 6
解释：选出任意 2 条边都可以连接所有城市，我们从中选取成本最小的 2 条。

示例 2：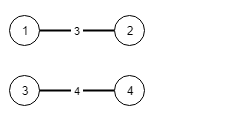

输入：n = 4, conections = [[1,2,3],[3,4,4]]
输出： -1
解释：即使连通所有的边，也无法连接所有城市。

提示：

$1<=n<=104$
$1<=connections.length<=104$
$connections[i].length==3$
$1<=xi,yi<=n$
$xi!=yi$
$0<=costi<=105$

题解：

从全局上看，该题的核心就是——用最小的代价让所有节点（城市）互相连通。在图论里，这就是「最小生成树」（Minimum Spanning Tree, MST）挑战。

核心思想可以浓缩为两句话：

• 只选能连通新城市的边：不断用代价最小、能增加图连通性的那条边扩展已有的网络。
• 多余的，会浪费成本。就是避免形成回路：一旦出现闭环，就说明那条边

以 Kruskal 为例的思路

• 按边权从小到大排序 最便宜的连接优先考虑。

• 并查集判连通 每次加入一条边，只有当它连接了两个尚不在同一连通分量的城市时才真正采用。

• 重复直到形成 n−1 条边 此时正好连接了全部 n 个城市且无环，成本最小。

代码实现

import java.util.*;
public class MSTConnector
{
// 并查集（Disjoint Set Union，支持路径压缩和按大小合并）
static class DSU
{
int[] parent;
// parent[i] 表示节点 i 的父节点
int[] size;
// size[i] 表示以 i 为根的集合大小
// 构造函数：初始化 n 个独立的集合
DSU(int n) {
parent = new int[n];
size = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
// 每个节点的父节点初始化为自己
size[i] = 1;
// 每个集合大小初始为 1
}
}
// 查找 x 所在集合的根节点（路径压缩）
int find(int x) {
while (x != parent[x]) {
parent[x] = parent[parent[x]];
// 压缩路径，加快后续查询
x = parent[x];
}
return x;
}
// 合并 a 和 b 所在的集合（按集合大小合并）
boolean union(int a, int b) {
int ra = find(a), rb = find(b);
if (ra == rb) return false;
// 已在同一集合，不合并
if (size[ra] < size[rb]) {
int t = ra; ra = rb; rb = t;
// 保证 ra 的集合较大
}
parent[rb] = ra;
// 将较小集合合并到较大集合
size[ra] += size[rb];
return true;
}
}
/**
* Kruskal 算法求最小生成树的总成本
* @param n 城市数量
* @param connections 每条连接 [城市1, 城市2, 成本]
* @return 最小总成本；若无法连通所有城市返回 -1
*/
public static int minimumCostKruskal(int n, int[][] connections) {
if (n <= 1) return 0;
// 没有城市或只有一个城市，不需要连接
// 将边转成 [cost, u, v] 格式，并忽略自环
List<
int[]> edges = new ArrayList<
>();
for (int[] e : connections) {
int x = e[0], y = e[1], c = e[2];
if (x == y) continue;
// 忽略自环
edges.add(new int[]{c, x - 1, y - 1
});
// 转换为 0-based 索引
}
// 按照成本升序排序
edges.sort(Comparator.comparingInt(a -> a[0]));
DSU dsu = new DSU(n);
// 初始化并查集
long total = 0;
// 累加总成本
int used = 0;
// 已选用的边数量
// 遍历所有边，贪心选择能连通两个不同集合的最小边
for (int[] e : edges) {
int c = e[0], u = e[1], v = e[2];
if (dsu.union(u, v)) {
// 如果连接了两个不同集合
total += c;
used++;
if (used == n - 1) return (int) total;
// 已构成生成树
}
}
return -1;
// 遍历完仍未连通所有城市
}
public static void main(String[] args) {
int n = 4;
int[][] connections = {
{
1, 2, 3
},
{
2, 3, 4
},
{
3, 4, 5
},
{
1, 4, 10
},
{
2, 4, 6
}
};
// Kruskal 输出
System.out.println(minimumCostKruskal(n, connections));
// 输出 12
// Prim 输出
System.out.println(minimumCostPrim(n, connections));
// 输出 12
}
/**
* Prim 算法求最小生成树的总成本
* @param n 城市数量
* @param connections 每条连接 [城市1, 城市2, 成本]
* @return 最小总成本；若无法连通所有城市返回 -1
*/
public static int minimumCostPrim(int n, int[][] connections) {
if (n <= 1) return 0;
// 构建邻接表，每个元素是 (cost, 目标城市)
List<
int[]>
[] adj = new ArrayList[n];
for (int i = 0; i < n; i++) adj[i] = new ArrayList<
>();
// 添加无向边
for (int[] e : connections) {
int x = e[0], y = e[1], c = e[2];
if (x == y) continue;
// 忽略自环
int u = x - 1, v = y - 1;
adj[u].add(new int[]{c, v
});
adj[v].add(new int[]{c, u
});
}
boolean[] visited = new boolean[n];
// 标记已加入生成树的城市
PriorityQueue<
int[]> pq = new PriorityQueue<
>(Comparator.comparingInt(a -> a[0]));
long total = 0;
// 累加总成本
int count = 1;
// 已访问城市数
// 从 0 号城市出发，将它的所有边加入最小堆
visited[0] = true;
for (int[] edge : adj[0]) pq.offer(edge);
// 不断从堆中取最小边扩展
while (!pq.isEmpty() && count < n) {
int[] top = pq.poll();
int c = top[0], v = top[1];
if (visited[v]) continue;
// 城市已访问，跳过
visited[v] = true;
count++;
total += c;
for (int[] edge : adj[v]) pq.offer(edge);
// 加入新城市的边
}
return count == n ? (int) total : -1;
// 判断是否连通
}
}

运行结果