ACAM 学习笔记 | 附 YbtOJ 全部题解

怎么有人现在才学 ACAM 呢。
好像比 SAM 简单挺多啊，也不记得当时是哪里看不懂。

AC 自动机（✔） 自动 AC 机（✘）

概述

ACAM(Aho–Corasick Automaton)，是用来解决多模式串匹配的字符串算法。它的结构是个 DAG，其中点表示状态，边表示转移。这一点上各种自动机都是相同的。
具体来说，可以感性理解为在 Trie 树上构建失配指针跑 KMP。

前置知识

• Trie。
  KMP 会不会都可以，虽然听起来离谱但我貌似就不怎么会。

状态

已经说过大致思想是在 Trie 上跑 KMP，我们肯定先把若干模式串都放进一棵 Trie 里。那么在这棵 Trie 上的每个节点，就代表着从根到这个点的字符串。我们把一个节点称作一个状态。
状态已经建完了，接下来要做的事情就是确定状态之间的转移，即在它们之间连一些边。

Fail 指针

定义

Fail 指针的作用，是在当前节点失配后，尝试只取当前字符串的一段后缀，使它能继续匹配。点 \(u\) 的 Fail 指针 \(\text{Fail}(u)\) 定义为 状态 \(u\) 作为某个模式串前缀出现的 最长后缀。
换句话说，这就是我们失配后要转移去的节点。大概长成这个样子：

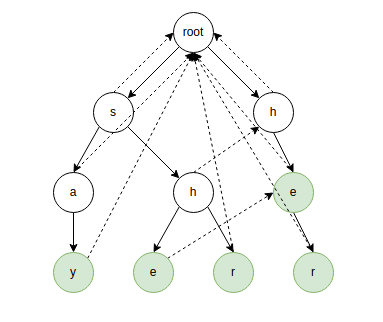
构建

根据定义，任何一个点的 Fail 指针指向的点深度都比自己小。考虑 bfs 按层构建 Fail 指针，这样可以保证深度比 \(u\) 小的点均已经构建完毕。
那么我们考虑根据父亲的 Fail 来构建该点的信息。设该点为 \(u\)，连向父亲的边字符为 \(c\)，那么基本的思想是这样的：

• 若 \(\text{Fail}(fa)\) 存在一个字符 \(c\) 的转移边，令 \(\text{Fail}(u)=ch[\text{Fail}(fa)][c]\)；
• 否则令 \(fa=\text{Fail}(fa)\)。
• 若最后就是找不到，\(\text{Fail}(u)=0\)。

考虑这样做为什么是对的。根据定义，\(\text{Fail}(fa)\) 是 \(fa\) 在 Trie 里存在的最长的后缀。那么如果 \(\text{Fail}(fa)\) 存在向 \(c\) 的转移边，在 \(\text{Fail}(fa)\) 后面接一个字符 \(c\) 也是 \(u\) 的最长后缀。
不存在时，考虑跳 Fail 取更短的后缀，跳到第一个匹配成功的就是能匹配的最长后缀。

事实上这样做每次都要跳很多次 Fail 指针，时间复杂度是不正确的。因此实际写代码时我们并不会这么写，需要用到下文的优化。

Trie 图

上述做法的瓶颈在不断跳 Fail 指针的过程。而每次匹配时，在同一个状态的同一字符处失配，Fail 最后跳到的位置是固定的。或许可以直接记录每个点最后跳到的位置。
先上代码：

queue<int> q;
for(int i=0;i<26;i++) if(d[0].s[i]) q.push(d[0].s[i]);
while(!q.empty())
{
    int u=q.front(); q.pop();
    for(int i=0;i<26;i++) 
    {
        if(!d[u].s[i]) d[u].s[i]=d[d[u].nxt].s[i];
        else d[d[u].s[i]].nxt=d[d[u].nxt].s[i],q.push(d[u].s[i]);
    }
}

发现如果 \(u\) 没有 \(i\) 这条转移边，根据上文说的我们应该不断跳 Fail 指针。但是这里我们直接连一条边到它父亲的 Fail 的对应位置。这是因为父亲的对应位置如果并没有 Trie 边，它也已经通过这个操作连到了第一个它能匹配的点。因此只需要跳一步就可以了。

那么对于这样实际不存在的边 \(u\to d[u][c]\)，表示如果 \(u\) 因为添加字符 \(c\) 而失配，应该跳转到 \(d[u][c]\)，省去了中间不合法的跳 Fail 指针的过程。

但是 Fail 指针依然有它的作用，Fail 是在能够匹配的情况下去找下一个后缀，而上文的边只有在失配时才能跳。

匹配

int solve(char *s)
{
    int len=strlen(s+1),ans=0,now=0;
    for(int i=1;i<=len;i++)
    {
        now=d[now].s[s[i]-'a'];
        for(int j=now;j&&d[j].cnt!=-1;j=d[j].nxt) ans+=d[j].cnt,d[j].cnt=-1;
    }
    return ans;
}

跳 Fail 指针即可。在这段代码里，已经统计过答案的点不会被多次访问，因此时间复杂度正确。

拓扑优化

说是拓扑优化其实跟拓扑没什么关系的啦。
若问题改为统计出现次数，已经统计过答案的点就需要多次访问，失去了时间复杂度的保证。
这里考虑把点和它的 Fail 指针连边。因为 Fail 的深度都小于它，所以容易证明这是一棵树。每次我们需要修改的是 某个点和它在 Fail 树上所有祖先的权值，所以只在点上记录修改操作，最后一起合并答案即可。
最后一起合并答案的时候可以用拓扑排序，也可以建树后 dfs。

拓扑

void tp()
{
	queue<int> q;
	for(int i=1;i<=tot;i++) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.front(); q.pop();
		if(tr[u].nxt) 
		{
			f[tr[u].nxt]+=f[u],in[tr[u].nxt]--;
			if(!in[tr[u].nxt]) q.push(tr[u].nxt);
		}
	}
}

dfs

void dfs(int u) {for(auto v:e[u]) dfs(v),f[u]+=f[v];}
for(int i=1;i<=tot;i++) e[d[i].nxt].push_back(i); //build tree

时刻分清操作在 Fail 树 还是 Trie 树上面。

YbtOJ 题解

代码懒得粘，可以找我要。

A.【例题1】单词查询|P3808【模板】AC自动机（简单版）

板子。

B.【例题2】单词频率|P3796【模板】AC自动机（加强版）

板子*2。一年前的提交记录是写得很抽象的拓扑优化，我猜不是我自己写的 /oh

C.【例题3】前缀匹配

由模板 1 我们知道了统计 Trie 上哪些节点被访问过的方法。那么这题就是对每个查询串沿着 Trie 走，找最深的被访问过的点即可。

D.【例题4】屏蔽词删除|P3121 [USACO15FEB] Censoring G

题面和原题一模一样，不截图了。
发现删了一个词之后会形成一些新的屏蔽词，我们要做到把 AC 自动机上的匹配状态还原到这个词出现以前的状态继续匹配。而这个词出现以前那个状态可能也被删了，因此不能简单地记录 pos。
使用栈来维护当前位置和在原串的下标，每次匹配到屏蔽词就弹栈即可还原状态。

E.【例题5】病毒代码|P2444 [POI2000] 病毒

题面同原题。
这道题是希望构造一个字符串，使它在 ACAM 上一直匹配不到出现过的子串。考虑它在 ACAM 上怎么走，实际就是走一个无限长的路径，其中路径上的点不经过任何模式串。
那也就是 ACAM 上存在一个满足上述条件的环。对不经过特殊点的转移建图，dfs 找环。
但考虑原来的正常匹配过程，我们需要每走到一个点都跳一遍它的所有 Fail。所以一个点的 Fail 是特殊点，它也不能走，这个可以在 getfail 的过程中处理。

F. 1.组合攻击|P3041[USACO12JAN] Video Game G

构造一个长度为 \(k\) 的字符串使匹配次数最多，观察到 \(k\) 和字符串总长都很小。暴力 dp，设 \(f_{i,j}\) 表示前 \(i\) 个字符匹配到 \(j\) 的最大匹配次数，枚举边转移。

G. 2.单词记忆|JZOJ5167

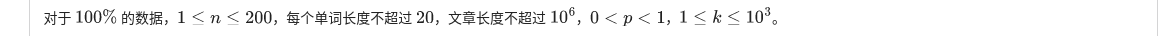
注意这里的“以 \(p\) 概率保留”，是所有的最小值一起的，要保留一起保留，不是分别以 \(p\) 的概率。
发现前后无关（缝合怪），ACAM 跑出每个串的出现次数。设 \(f_{i,j}\) 表示前 \(i\) 轮，有 \(j\) 轮忘记了的概率。
有转移：\(f_{i,j}=f_{i-1,j-1}\times (1-p)+f_{i-1,j}\times p\)。
那么出现次数第 \(x\) 小的单词没被忘的概率就是 \(\sum\limits_{i=0}^{x-1} f_{k,i}\)。

H. 3.字符串计数|P5357【模板】AC自动机（二次加强版）

板子*3。好多板子。
突然想到既然拓扑优化放在这个地方岂不是前面的题不写拓扑优化都能过？输麻了。

I. 4.文本生成器|P4052 [JSOI2007] 文本生成器

考虑把限制反过来，求长度为 \(m\) 且不能匹配任何模式串的文本串个数。设 \(f_{i,j}\) 表示前 \(i\) 位匹配到 \(j\)，未经过特殊点的方案数。
在 ACAM 上跑转移边，累加答案即可。

J. 5.最短字符串

没找到原题，有没有神仙帮忙找找。
发现 \(n\) 很小，可以状压哪些子串已经出现过。设 \(f_{i,j,k}\) 表示前 \(i\) 位，匹配到 \(j\)，\(k\) 集合内的子串出现过 的情况是否存在。
dp 过程中发现合法解就 break。

其他例题

放点感觉比较厉害的题。
一本通为了符合 NOIP 难度定位题选得还是板了点。

CF547E Mike and Friends

首先有个结论，对于 trie 上的两个前缀 \(s,t\)，\(s\) 在 \(t\) 中的出现次数等于（\(t\) 在 Trie 树上的祖先）在 Fail 树中 \(s\) 的子树里的点数。
考虑为什么是这样：点 \(x\) 在 Fail 树的 \(s\) 子树里，说明 \(s\) 是 \(x\) 的后缀。而枚举祖先的过程就等同于枚举 \(s\) 在 \(t\) 中的结束位置。
那么 \(s_k\) 在 \(s_l\dots s_r\) 中的出现次数可以拆成 \([1,l-1]\) 和 \([1,r]\) 两个前缀询问。每次询问一个子树的和，即在 dfn 序上区间求和，使用 BIT 维护。
修改次数为所有字符串总长度，即 \(\sum |s_i|\)。设这个值为 \(S\)。那么时间复杂度是 \(O((S+m)\log S)\)。

CF587F Duff is Mad

和上面一题题意迷之相似（？/youl
建 ACAM，这里算 \(s\) 在 \(t\) 里的出现次数时把上面的结论反过来：给 \(s\) Fail 子树里的每个点权值加 \(1\)，求 \(t\) 在 Trie 树上所有祖先的权值和。
离线下来以 \(O(len_k \log len_k)\) 的复杂度处理一个询问是容易的，BIT 维护 dfn 序，区间修改单点查询。
但如果多次询问一个 \(len_k\) 很大的点，不能用上面的方法维护。
考虑根号分治，对于所有 \(len>B\) 的 \(k\)，以 \(O(n)\) 的复杂度处理与它相关的所有询问。具体方法是把结论反回去，用上面那题的结论处理这个就可以了。

CF590E Birthday

如果 \(a\) 是 \(b\) 的子串，就连边 \(b\to a\)。那么这张图形成了 DAG，找图的最长反链即可，可以参照 [CTSC2008] 祭祀。
显然这个题难点在后面一半，但这里是 ACAM 学习笔记，所以要讲怎么连边。
肯定是不能暴力在 ACAM 上跳 Fail 的，我们要路径压缩，对每个点记一个 to 表示它一直跳 Fail 跳到的第一个子串。这个东西可以在 getfail 的过程中用类似的方式处理。
那么对于一个串找它的子串，就是在 Trie 树上枚举子串所有可能的结尾位置 \(x\)，连边 \(x\to to_x\)。卡空间，实现时不要递归。