「解题报告」CSP - S 2019

总分：100 + 55 + 10 + 32 + 12 + 40 = 249。

[CSP-S2019] 格雷码

题目描述

通常，人们习惯将所有 \(n\) 位二进制串按照字典序排列，例如所有 2 位二进制串按字典序从小到大排列为：00，01，10，11。

格雷码（Gray Code）是一种特殊的 \(n\) 位二进制串排列法，它要求相邻的两个二进制串间恰好有一位不同，特别地，第一个串与最后一个串也算作相邻。

所有 2 位二进制串按格雷码排列的一个例子为：00，01，11，10。

\(n\) 位格雷码不止一种，下面给出其中一种格雷码的生成算法：

1 位格雷码由两个 1 位二进制串组成，顺序为：0，1。
\(n + 1\) 位格雷码的前 \(2^n\) 个二进制串，可以由依此算法生成的 \(n\) 位格雷码（总共 \(2^n\) 个 \(n\) 位二进制串）按顺序排列，再在每个串前加一个前缀 0 构成。
\(n + 1\) 位格雷码的后 \(2^n\) 个二进制串，可以由依此算法生成的 \(n\) 位格雷码（总共 \(2^n\) 个 \(n\) 位二进制串）按逆序排列，再在每个串前加一个前缀 1 构成。

综上，\(n + 1\) 位格雷码，由 \(n\) 位格雷码的 \(2^n\) 个二进制串按顺序排列再加前缀 0，和按逆序排列再加前缀 1 构成，共 \(2^{n+1}\) 个二进制串。另外，对于 \(n\) 位格雷码中的 \(2^n\) 个二进制串，我们按上述算法得到的排列顺序将它们从 \(0 \sim 2^n - 1\) 编号。

按该算法，2 位格雷码可以这样推出：

已知 1 位格雷码为 0，1。
前两个格雷码为 00，01。后两个格雷码为 11，10。合并得到 00，01，11，10，编号依次为 0 ~ 3。

同理，3 位格雷码可以这样推出：

已知 2 位格雷码为：00，01，11，10。
前四个格雷码为：000，001，011，010。后四个格雷码为：110，111，101，100。合并得到：000，001，011，010，110，111，101，100，编号依次为 0 ~ 7。

现在给出 \(n\)，\(k\)，请你求出按上述算法生成的 \(n\) 位格雷码中的 \(k\) 号二进制串。

输入格式

仅一行两个整数 \(n\)，\(k\)，意义见题目描述。

输出格式

仅一行一个 \(n\) 位二进制串表示答案。

样例 #1

样例输入 #1

2 3

样例输出 #1

样例 #2

样例输入 #2

3 5

样例输出 #2

样例 #3

样例输入 #3

44 1145141919810

样例输出 #3

00011000111111010000001001001000000001100011

提示

【样例 1 解释】

2 位格雷码为：00，01，11，10，编号从 0∼3，因此 3 号串是 10。

【样例 2 解释】

3 位格雷码为：000，001，011，010，110，111，101，100，编号从 0∼7，因此 5 号串是 111。

【数据范围】

对于 \(50\%\) 的数据：\(n \leq 10\)

对于 \(80\%\) 的数据：\(k \leq 5 \times 10^6\)

对于 \(95\%\) 的数据：\(k \leq 2^{63} - 1\)

对于 \(100\%\) 的数据：\(1 \leq n \leq 64\), \(0 \leq k \lt 2^n\)

一个很简单的二分思想，判断位置是在前半段还是后半段，然后二分。

// The code was written by yifan, and yifan is neutral!!!

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))
using ull = unsigned long long;

template<typename T>
inline T read() {
	T x = 0;
	bool fg = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		fg |= (ch == '-');
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 3) + (x << 1) + (ch ^ 48);
		ch = getchar();
	}
	return fg ? ~x + 1 : x; 
}

ull k, n;

void solve(int dig, ull pos) {
	if (dig == 0) {
		return ;
	}
	if (pos >= (1ull << (dig - 1))) {
		cout << "1";
		solve(dig - 1, (1ull << (dig - 1)) - pos + (1ull << (dig - 1)) - 1);
	} else {
		cout << "0";
		solve(dig - 1, pos);
	}
}

int main() {
	n = read<int>(), k = read<ull>();
	solve(n, k);
	return 0;
}

[CSP-S2019] 括号树

题目背景

本题中合法括号串的定义如下：

() 是合法括号串。
如果 A 是合法括号串，则 (A) 是合法括号串。
如果 A，B 是合法括号串，则 AB 是合法括号串。

本题中子串与不同的子串的定义如下：

字符串 S 的子串是 S 中连续的任意个字符组成的字符串。S 的子串可用起始位置 \(l\) 与终止位置 \(r\) 来表示，记为 \(S (l, r)\)（\(1 \leq l \leq r \leq |S |\)，\(|S |\) 表示 S 的长度）。
S 的两个子串视作不同当且仅当它们在 S 中的位置不同，即 \(l\) 不同或 \(r\) 不同。

题目描述

一个大小为 \(n\) 的树包含 \(n\) 个结点和 \(n - 1\) 条边，每条边连接两个结点，且任意两个结点间有且仅有一条简单路径互相可达。

小 Q 是一个充满好奇心的小朋友，有一天他在上学的路上碰见了一个大小为 \(n\) 的树，树上结点从 \(1 \sim n\) 编号，\(1\) 号结点为树的根。除 \(1\) 号结点外，每个结点有一个父亲结点，\(u\)（\(2 \leq u \leq n\)）号结点的父亲为 \(f_u\)（\(1 ≤ f_u < u\)）号结点。

小 Q 发现这个树的每个结点上恰有一个括号，可能是( 或)。小 Q 定义 \(s_i\) 为：将根结点到 \(i\) 号结点的简单路径上的括号，按结点经过顺序依次排列组成的字符串。

显然 \(s_i\) 是个括号串，但不一定是合法括号串，因此现在小 Q 想对所有的 \(i\)（\(1\leq i\leq n\)）求出，\(s_i\) 中有多少个互不相同的子串是合法括号串。

这个问题难倒了小 Q，他只好向你求助。设 \(s_i\) 共有 \(k_i\) 个不同子串是合法括号串，你只需要告诉小 Q 所有 \(i \times k_i\) 的异或和，即：

\[(1 \times k_1)\ \text{xor}\ (2 \times k_2)\ \text{xor}\ (3 \times k_3)\ \text{xor}\ \cdots\ \text{xor}\ (n \times k_n) \]

其中 \(xor\) 是位异或运算。

输入格式

第一行一个整数 \(n\)，表示树的大小。

第二行一个长为 \(n\) 的由( 与) 组成的括号串，第 \(i\) 个括号表示 \(i\) 号结点上的括号。

第三行包含 \(n − 1\) 个整数，第 \(i\)（\(1 \leq i \lt n\)）个整数表示 \(i + 1\) 号结点的父亲编号 \(f_{i+1}\)。

输出格式

仅一行一个整数表示答案。

样例 #1

样例输入 #1

5
(()()
1 1 2 2

样例输出 #1

提示

【样例解释1】

树的形态如下图：

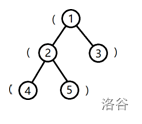
将根到 1 号结点的简单路径上的括号，按经过顺序排列所组成的字符串为 (，子串是合法括号串的个数为 \(0\)。

将根到 2 号结点的字符串为 ((，子串是合法括号串的个数为 \(0\)。

将根到 3 号结点的字符串为 ()，子串是合法括号串的个数为 \(1\)。

将根到 4 号结点的字符串为 (((，子串是合法括号串的个数为 \(0\)。

将根到 5 号结点的字符串为 (()，子串是合法括号串的个数为 \(1\)。

【数据范围】

说实话，我并不知道我打的啥 = =

好像是数组 + 指针 + dfs 回溯？但肯定打挂了……~~不然就过了，55分纯属走运了吧~~

// The code was written by yifan, and yifan is neutral!!!

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))

template<typename T>
inline T read() {
    T x = 0;
    bool fg = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        fg |= (ch == '-');
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return fg ? ~x + 1 : x;
}

const int N = 5e5 + 5;

int pos0, n;
ll res;
int fa[N], cnt[N];
char s[N];
ll ans[N];
vector<int> e[N];

void dfs(int u) {
	ll tmp = res, tmp2;
	if (s[u] == '(') {
		ans[u] = u * res;
		++ cnt[pos0 ++];
	} else {
		if (pos0 != 0) {
			res += cnt[pos0 - 1];
		}
		ans[u] = u * res;
		if (pos0) {
			tmp2 = cnt[pos0];
			cnt[pos0 --] = 0;
		} else {
			res = 0;
		}
	}
	for (int v : e[u]) {
		dfs(v);
	}
	if (s[u] == '(') {
		cnt[-- pos0] --;
	} else {
		if (res) {
			cnt[++ pos0] = tmp2;
		}
	}
	res = tmp;
}

int main() {
	n = read<int>();
	scanf("%s", s + 1);
	rep (i, 2, n, 1) {
		fa[i] = read<int>();
		e[fa[i]].emplace_back(i);
	}
	dfs(1);
	ll Ans = 0;
	rep (i, 1, n, 1) {
		Ans ^= ans[i];
	}
	cout << Ans << '\n';
    return 0;
}

[CSP-S2019] 树上的数

题目描述

给定一个大小为 \(n\) 的树，它共有 \(n\) 个结点与 \(n - 1\) 条边，结点从 \(1 \sim n\) 编号。初始时每个结点上都有一个 \(1 \sim n\) 的数字，且每个 \(1 \sim n\) 的数字都只在恰好一个结点上出现。

接下来你需要进行恰好 \(n - 1\) 次删边操作，每次操作你需要选一条未被删去的边，此时这条边所连接的两个结点上的数字将会交换，然后这条边将被删去。

\(n - 1\) 次操作过后，所有的边都将被删去。此时，按数字从小到大的顺序，将数字 \(1 \sim n\) 所在的结点编号依次排列，就得到一个结点编号的排列 \(P_i\)。现在请你求出，在最优操作方案下能得到的字典序最小的 \(P_i\)。

如上图，蓝圈中的数字 \(1 \sim 5\) 一开始分别在结点②、①、③、⑤、④。按照 (1)(4)(3)(2) 的顺序删去所有边，树变为下图。按数字顺序得到的结点编号排列为①③④②⑤，该排列是所有可能的结果中字典序最小的。

输入格式

本题输入包含多组测试数据。

第一行一个正整数 \(T\)，表示数据组数。

对于每组测试数据：

第一行一个整数 \(n\)，表示树的大小。

第二行 \(n\) 个整数，第 \(i (1 \leq i \leq n)\) 个整数表示数字 \(i\) 初始时所在的结点编号。

接下来 \(n - 1\) 行每行两个整数 \(x\), \(y\)，表示一条连接 \(x\) 号结点与 \(y\) 号结点的边。

输出格式

对于每组测试数据，输出一行共 \(n\) 个用空格隔开的整数，表示最优操作方案下所能得到的字典序最小的 \(P_i\)。

样例 #1

样例输入 #1

4
5
2 1 3 5 4
1 3
1 4
2 4
4 5
5
3 4 2 1 5
1 2
2 3
3 4
4 5
5
1 2 5 3 4
1 2
1 3
1 4
1 5
10
1 2 3 4 5 7 8 9 10 6
1 2
1 3
1 4
1 5
5 6
6 7
7 8
8 9
9 10

样例输出 #1

1 3 4 2 5
1 3 5 2 4
2 3 1 4 5
2 3 4 5 6 1 7 8 9 10

提示

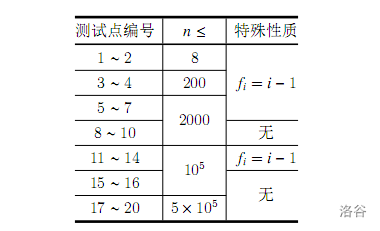
【数据范围】

测试点编号	\(n \leq\)	特殊性质
\(1 \sim 2\)	10	无
\(3 \sim 4\)	160	树的形态是一条链
\(5 \sim 7\)	2000	同上
\(8 \sim 9\)	160	存在度数为 \(n - 1\) 的结点
\(10 \sim 12\)	2000	同上
\(13 \sim 16\)	160	无
\(17 \sim 20\)	2000	无

对于所有测试点：\(1 \leq T \leq 10\)，保证给出的是一个树。

一道黑……

最纯粹的暴力，枚举删边的顺序即可，有 \(10\) 分的好成绩……

// The code was written by yifan, and yifan is neutral!!!

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))

template<typename T>
inline T read() {
    T x = 0;
    bool fg = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        fg |= (ch == '-');
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return fg ? ~x + 1 : x;
}

const int N = 2010;

using tii = tuple<int, int>;

int T, n;
int val[N], tmp[N], ans[N];
bool vis[N];
tii e[N];

void work() {
	sort(tmp + 1, tmp + n + 1, [](int x, int y) {
		return val[x] < val[y];
	});
	rep (i, 1, n, 1) {
		if (ans[i] > tmp[i]) {
			rep (j, 1, n, 1) {
				ans[j] = tmp[j];
			}
			return ;
		}
		if (ans[i] < tmp[i]) {
			return ;
		}
	}
}

void dfs(int x) {
	if (x == n) {
		work();
		return ;
	}
	int u, v;
	rep (i, 1, n - 1, 1) {
		if (vis[i])	continue ;
		vis[i] = 1;
		tie(u, v) = e[i];
		swap(val[u], val[v]);
		dfs(x + 1);
		swap(val[u], val[v]);
		vis[i] = 0;
	}
}

void solve() {
	n = read<int>();
	rep (i, 1, n, 1) {
		int x = read<int>();
		tmp[i] = val[x] = i;
		ans[i] = n;
	}
	int x, y;
	rep (i, 1, n - 1, 1) {
		x = read<int>(), y = read<int>();
		e[i] = make_tuple(x, y);
		vis[i] = 0;
	}
	dfs(1);
	rep (i, 1, n, 1) {
		cout << ans[i] << ' ';
	}
	putchar('\n');
}

int main() {
	T = read<int>();
	while (T --) {
		solve();
	}
    return 0;
}

[CSP-S2019] Emiya 家今天的饭

题目描述

Emiya 是个擅长做菜的高中生，他共掌握 \(n\) 种烹饪方法，且会使用 \(m\) 种主要食材做菜。为了方便叙述，我们对烹饪方法从 \(1 \sim n\) 编号，对主要食材从 \(1 \sim m\) 编号。

Emiya 做的每道菜都将使用恰好一种烹饪方法与恰好一种主要食材。更具体地，Emiya 会做 \(a_{i,j}\) 道不同的使用烹饪方法 \(i\) 和主要食材 \(j\) 的菜（\(1 \leq i \leq n\)、\(1 \leq j \leq m\)），这也意味着 Emiya 总共会做 \(\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m} a_{i,j}\) 道不同的菜。

Emiya 今天要准备一桌饭招待 Yazid 和 Rin 这对好朋友，然而三个人对菜的搭配有不同的要求，更具体地，对于一种包含 \(k\) 道菜的搭配方案而言：

Emiya 不会让大家饿肚子，所以将做至少一道菜，即 \(k \geq 1\)
Rin 希望品尝不同烹饪方法做出的菜，因此她要求每道菜的烹饪方法互不相同
Yazid 不希望品尝太多同一食材做出的菜，因此他要求每种主要食材至多在一半的菜（即 \(\lfloor \frac{k}{2} \rfloor\) 道菜）中被使用

这里的 \(\lfloor x \rfloor\) 为下取整函数，表示不超过 \(x\) 的最大整数。

这些要求难不倒 Emiya，但他想知道共有多少种不同的符合要求的搭配方案。两种方案不同，当且仅当存在至少一道菜在一种方案中出现，而不在另一种方案中出现。

Emiya 找到了你，请你帮他计算，你只需要告诉他符合所有要求的搭配方案数对质数 \(998,244,353\) 取模的结果。

输入格式

第 1 行两个用单个空格隔开的整数 \(n,m\)。

第 2 行至第 \(n + 1\) 行，每行 \(m\) 个用单个空格隔开的整数，其中第 \(i + 1\) 行的 \(m\) 个数依次为 \(a_{i,1}, a_{i,2}, \cdots, a_{i,m}\)。

输出格式

仅一行一个整数，表示所求方案数对 \(998,244,353\) 取模的结果。

样例 #1

样例输入 #1

2 3 
1 0 1
0 1 1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

样例 #3

样例输入 #3

样例输出 #3

提示

【样例 1 解释】

由于在这个样例中，对于每组 \(i, j\)，Emiya 都最多只会做一道菜，因此我们直接通过给出烹饪方法、主要食材的编号来描述一道菜。

符合要求的方案包括：

做一道用烹饪方法 1、主要食材 1 的菜和一道用烹饪方法 2、主要食材 2 的菜
做一道用烹饪方法 1、主要食材 1 的菜和一道用烹饪方法 2、主要食材 3 的菜
做一道用烹饪方法 1、主要食材 3 的菜和一道用烹饪方法 2、主要食材 2 的菜

因此输出结果为 \(3 \bmod 998,244,353 = 3\)。需要注意的是，所有只包含一道菜的方案都是不符合要求的，因为唯一的主要食材在超过一半的菜中出现，这不满足 Yazid 的要求。

【样例 2 解释】

Emiya 必须至少做 2 道菜。

做 2 道菜的符合要求的方案数为 100。

做 3 道菜的符合要求的方案数为 90。

因此符合要求的方案数为 100 + 90 = 190。

【数据范围】

测试点编号	\(n=\)	\(m=\)	\(a_{i,j}<\)	测试点编号	\(n=\)	\(m=\)	\(a_{i,j}<\)
\(1\)	\(2\)	\(2\)	\(2\)	\(7\)	\(10\)	\(2\)	\(10^3\)
\(2\)	\(2\)	\(3\)	\(2\)	\(8\)	\(10\)	\(3\)	\(10^3\)
\(3\)	\(5\)	\(2\)	\(2\)	\(9\sim 12\)	\(40\)	\(2\)	\(10^3\)
\(4\)	\(5\)	\(3\)	\(2\)	\(13\sim 16\)	\(40\)	\(3\)	\(10^3\)
\(5\)	\(10\)	\(2\)	\(2\)	\(17\sim 21\)	\(40\)	\(500\)	\(10^3\)
\(6\)	\(10\)	\(3\)	\(2\)	\(22\sim 25\)	\(100\)	\(2\times 10^3\)	\(998244353\)

对于所有测试点，保证 \(1 \leq n \leq 100\)，\(1 \leq m \leq 2000\)，\(0 \leq a_{i,j} \lt 998,244,353\)。

dfs 搜索，很纯粹的暴力，由于题目给的限制条件很多，所以搜索的时候复杂度就被剪下来了，能拿到 \(32\) 分的好成绩。

// The code was written by yifan, and yifan is neutral!!!

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))

template<typename T>
inline T read() {
    T x = 0;
    bool fg = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        fg |= (ch == '-');
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return fg ? ~x + 1 : x;
}

const int N = 110;
const int M = 2e3 + 5;
const int mod = 998244353;

int n, m, limt;
ll ans;
ll a[N][M], cnt[M];
bool used[N];
vector<ll> food;

void dfs(int rest, int beg) {
	if (rest == 0) {
		ll res = 1;
		for (ll v : food) {
			res = res * v % mod;
		}
		ans = (ans + res) % mod;
		return ;
	}
	if (beg > n)	return ;
	rep (i, beg, n, 1) {
		rep (j, 1, m, 1) {
			if (cnt[j] >= limt)	continue ;
			food.emplace_back(a[i][j]);
			++ cnt[j];
			dfs(rest - 1, i + 1);
			food.pop_back();
			-- cnt[j];
		}
	}
}

int main() {
	n = read<int>(), m = read<int>();
	rep (i, 1, n, 1) {
		rep (j, 1, m, 1) {
			a[i][j] = read<int>();
		}
	}
	rep (i, 1, n, 1) {
		limt = (i >> 1);
		dfs(i, 1);
	}
	cout << ans << '\n';
    return 0;
}

[CSP-S2019] 划分

题目描述

2048 年，第三十届 CSP 认证的考场上，作为选手的小明打开了第一题。这个题的样例有 \(n\) 组数据，数据从 \(1 \sim n\) 编号，\(i\) 号数据的规模为 \(a_i\)。

小明对该题设计出了一个暴力程序，对于一组规模为 \(u\) 的数据，该程序的运行时间为 \(u^2\)。然而这个程序运行完一组规模为 \(u\) 的数据之后，它将在任何一组规模小于 \(u\) 的数据上运行错误。样例中的 \(a_i\) 不一定递增，但小明又想在不修改程序的情况下正确运行样例，于是小明决定使用一种非常原始的解决方案：将所有数据划分成若干个数据段，段内数据编号连续，接着将同一段内的数据合并成新数据，其规模等于段内原数据的规模之和，小明将让新数据的规模能够递增。

也就是说，小明需要找到一些分界点 \(1 \leq k_1 \lt k_2 \lt \cdots \lt k_p \lt n\)，使得

\[\sum_{i=1}^{k_1} a_i \leq \sum_{i=k_1+1}^{k_2} a_i \leq \cdots \leq \sum_{i=k_p+1}^{n} a_i \]

注意 \(p\) 可以为 \(0\) 且此时 \(k_0 = 0\)，也就是小明可以将所有数据合并在一起运行。

小明希望他的程序在正确运行样例情况下，运行时间也能尽量小，也就是最小化

\[(\sum_{i=1}^{k_1} a_i)^2 + (\sum_{i=k_1+1}^{k_2} a_i)^2 + \cdots + (\sum_{i=k_p+1}^{n} a_i)^2 \]

小明觉得这个问题非常有趣，并向你请教：给定 \(n\) 和 \(a_i\)，请你求出最优划分方案下，小明的程序的最小运行时间。

输入格式

由于本题的数据范围较大，部分测试点的 \(a_i\) 将在程序内生成。

第一行两个整数 \(n, type\)。\(n\) 的意义见题目描述，\(type\) 表示输入方式。

若 \(type = 0\)，则该测试点的 \(a_i\) 直接给出。输入文件接下来：第二行 \(n\) 个以空格分隔的整数 \(a_i\)，表示每组数据的规模。
若 \(type = 1\)，则该测试点的 \(a_i\) 将特殊生成，生成方式见后文。输入文件接下来：第二行六个以空格分隔的整数 \(x, y, z, b_1, b_2, m\)。接下来 \(m\) 行中，第 \(i (1 \leq i \leq m)\) 行包含三个以空格分隔的正整数 \(p_i, l_i, r_i\)。

对于 \(type = 1\) 的 23~25 号测试点，\(a_i\) 的生成方式如下：

给定整数 \(x, y, z, b_1, b_2, m\)，以及 \(m\) 个三元组 \((p_i, l_i, r_i)\)。

保证 \(n \geq 2\)。若 \(n \gt 2\)，则 \(\forall 3 \leq i \leq n, b_i = (x \times b_{i−1} + y \times b_{i−2} + z) \mod 2^{30}\)。

保证 \(1 \leq p_i \leq n, p_m = n\)。令 \(p_0 = 0\)，则 \(p_i\) 还满足 \(\forall 0 \leq i \lt m\) 有 \(p_i \lt p_{i+1}\)。

对于所有 \(1 \leq j \leq m\)，若下标值 \(i (1 \leq i \leq n)\)满足 \(p_{j−1} \lt i \leq p_j\)，则有

\[a_i = \left(b_i \mod \left( r_j − l_j + 1 \right) \right) + l_j \]

上述数据生成方式仅是为了减少输入量大小，标准算法不依赖于该生成方式。

输出格式

输出一行一个整数，表示答案。

样例 #1

样例输入 #1

5 0
5 1 7 9 9

样例输出 #1

样例 #2

样例输入 #2

10 0
5 6 7 7 4 6 2 13 19 9

样例输出 #2

样例 #3

样例输入 #3

10000000 1
123 456 789 12345 6789 3
2000000 123456789 987654321
7000000 234567891 876543219
10000000 456789123 567891234

样例输出 #3

4972194419293431240859891640

提示

【样例 1 解释】

最优的划分方案为 \(\{5,1\}, \{7\}, \{9\}, \{9\}\)。由 \(5 + 1 \leq 7 \leq 9 \leq 9\) 知该方案合法。

答案为 \((5 + 1)^2 + 7^2 + 9^2 + 9^2 = 247\)。

虽然划分方案 \(\{5\}, \{1\}, \{7\}, \{9\}, \{9\}\) 对应的运行时间比 \(247\) 小，但它不是一组合法方案，因为 \(5 \gt 1\)。

虽然划分方案 \(\{5\}, \{1,7\}, \{9\}, \{9\}\) 合法，但该方案对应的运行时间为 \(251\)，比 \(247\) 大。

【样例 2 解释】

最优的划分方案为 \(\{5\}, \{6\}, \{7\}, \{7\}, \{4,6,2\}, \{13\}, \{19,9\}\)。

【数据范围】

测试点编号	\(n \leq\)	\(a_i \leq\)	\(type =\)
\(1 \sim 3\)	\(10\)	\(10\)	0
\(4 \sim 6\)	\(50\)	\(10^3\)	0
\(7 \sim 9\)	\(400\)	\(10^4\)	0
\(10 \sim 16\)	\(5000\)	\(10^5\)	0
\(17 \sim 22\)	\(5 \times 10^5\)	\(10^6\)	0
\(23 \sim 25\)	\(4 \times 10^7\)	\(10^9\)	1

对于\(type=0\)的所有测试点,保证最后输出的答案\(\leq 4 \times 10^{18}\)

所有测试点满足：\(type \in \{0,1\}\)，\(2 \leq n \leq 4 \times 10^7\)，\(1 \leq a_i \leq 10^9\)，\(1 \leq m \leq 10^5\)，\(1 \leq l_i \leq r_i \leq 10^9\)，\(0 \leq x,y,z,b_1,b_2 \lt 2^{30}\)。

还是 dfs 暴力枚举划分位置。

// The code was written by yifan, and yifan is neutral!!!

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))

template<typename T>
inline T read() {
    T x = 0;
    bool fg = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        fg |= (ch == '-');
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return fg ? ~x + 1 : x;
}

const int N = 5e5 + 5;

int n, type;
ll ans = 1e18;
ll a[N], sum[N];
vector<ll> val;

void work() {
	ll res = 0, las = 0;
	for (ll v : val) {
		if (v < las)	return ;
		res += v * v;
		las = v;
	}
	if (res < ans) {
		ans = res;
	}
}

void dfs(int las) {
	if (las > n)	return ;
	rep (i, las + 1, n, 1) {
		if (sum[i] - sum[las] > sum[n] - sum[i]) {
			val.emplace_back(sum[n] - sum[las]);
			work();
			val.pop_back();
			return ;
		} else {
			val.emplace_back(sum[i] - sum[las]);
			dfs(i);
			val.pop_back();
		}
	}
}

int main() {
	n = read<int>(), type = read<int>();
	rep (i, 1, n, 1) {
		a[i] = read<int>();
		sum[i] = sum[i - 1] + a[i];
	}
	dfs(0);
	cout << ans << '\n';
    return 0;
}

[CSP-S2019] 树的重心

题目描述

小简单正在学习离散数学，今天的内容是图论基础，在课上他做了如下两条笔记：

一个大小为 \(n\) 的树由 \(n\) 个结点与 \(n − 1\) 条无向边构成，且满足任意两个结点间有且仅有一条简单路径。在树中删去一个结点及与它关联的边，树将分裂为若干个子树；而在树中删去一条边（保留关联结点，下同），树将分裂为恰好两个子树。
对于一个大小为 \(n\) 的树与任意一个树中结点 \(c\)，称 \(c\) 是该树的重心当且仅当在树中删去 \(c\) 及与它关联的边后，分裂出的所有子树的大小均不超过 \(\lfloor \frac{n}{2} \rfloor\)（其中 \(\lfloor x \rfloor\) 是下取整函数）。对于包含至少一个结点的树，它的重心只可能有 1 或 2 个。

课后老师给出了一个大小为 \(n\) 的树 \(S\)，树中结点从 \(1 \sim n\) 编号。小简单的课后作业是求出 \(S\) 单独删去每条边后，分裂出的两个子树的重心编号和之和。即：

\[\sum_{(u,v) \in E} \left( \sum_{1 \leq x \leq n \atop 且 x 号点是 S'_u 的重心} x + \sum_{1 \leq y \leq n \atop 且 y 号点是 S'_v 的重心} y \right) \]

上式中，\(E\) 表示树 \(S\) 的边集，\((u,v)\) 表示一条连接 \(u\) 号点和 \(v\) 号点的边。\(S'_u\) 与 \(S'_v\) 分别表示树 \(S\) 删去边 \((u,v)\) 后，\(u\) 号点与 \(v\) 号点所在的被分裂出的子树。

小简单觉得作业并不简单，只好向你求助，请你教教他。

输入格式

本题包含多组测试数据

第一行一个整数 \(T\) 表示数据组数。

接下来依次给出每组输入数据，对于每组数据：

第一行一个整数 \(n\) 表示树 \(S\) 的大小。

接下来 \(n − 1\) 行，每行两个以空格分隔的整数 \(u_i\)，\(v_i\)，表示树中的一条边 \((u_i,v_i)\)。

输出格式

共 \(T\) 行，每行一个整数，第 \(i\) 行的整数表示：第 \(i\) 组数据给出的树单独删去每条边后，分裂出的两个子树的重心编号和之和。

样例 #1

样例输入 #1

样例输出 #1

32
56

提示

【样例 1 解释】

对于第一组数据：

删去边 \((1,2)\)，1 号点所在子树重心编号为 \(\{1\}\)，2 号点所在子树重心编号为 \(\{2,3\}\)。

删去边 \((2,3)\)，2 号点所在子树重心编号为 \(\{2\}\)，3 号点所在子树重心编号为 \(\{3,5\}\)。

删去边 \((2,4)\)，2 号点所在子树重心编号为 \(\{2,3\}\)，4 号点所在子树重心编号为 \(\{4\}\)。

删去边 \((3,5)\)，3 号点所在子树重心编号为 \(\{2\}\)，5 号点所在子树重心编号为 \(\{5\}\)。

因此答案为 \(1 + 2 + 3 + 2 + 3 + 5 + 2 + 3 + 4 + 2 + 5 = 32\)。

【数据范围】

测试点编号	\(n =\)	特殊性质
\(1 \sim 2\)	\(7\)	无
\(3 \sim 5\)	\(199\)	无
\(6 \sim 8\)	\(1999\)	无
\(9 \sim 11\)	\(49991\)	A
\(12 \sim 15\)	\(262143\)	B
\(16\)	\(99995\)	无
\(17 \sim 18\)	\(199995\)	无
\(19 \sim 20\)	\(299995\)	无

表中特殊性质一栏，两个变量的含义为存在一个 \(1 \sim n\) 的排列 \(p_i (1 \leq i \leq n)\)，使得：

A：树的形态是一条链。即 \(\forall 1 \leq i \lt n\)，存在一条边 \((p_i, p_{i + 1})\)。
B：树的形态是一个完美二叉树。即 \(\forall 1 \leq i \leq \frac{n-1}{2}\) ，存在两条边 \((p_i, p_{2i})\) 与 \((p_i, p_{2i+1})\)。

对于所有测试点：\(1 \leq T \leq 5 , 1 \leq u_i,v_i \leq n\)。保证给出的图是一个树。

比较暴力了。

枚举删边，进行 dfs 和 dp 来找树的重心。

// The code was written by yifan, and yifan is neutral!!!

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))

template<typename T>
inline T read() {
    T x = 0;
    bool fg = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        fg |= (ch == '-');
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return fg ? ~x + 1 : x;
}

const int N = 3e5 + 5;

using tii = tuple<int, int>;

int T, n, limx, limy;
ll ans;
int siz[N], dp[N];
vector<int> e[N];
vector<tii> E;

void init() {
	ans = 0;
	E.clear();
	rep (i, 1, n, 1) {
		e[i].clear();
	}
	memset(dp, 0, sizeof dp);
}

void dfs(int u, int fat) {
	siz[u] = 1;
	for (int v : e[u]) {
		if (v == fat || ((u == limx) && (v == limy)) || ((u == limy) && (v == limx)))	continue ;
		dfs(v, u);
		siz[u] += siz[v];
	}
}

void Dp(int u, int fat, int tp) {
	dp[u] = 0;
	for (int v : e[u]) {
		if (v == fat || ((u == limx) && (v == limy)) || ((u == limy) && (v == limx)))	continue ;
		Dp(v, u, tp);
		dp[u] = max(dp[u], siz[v]);
	}
	dp[u] = max(siz[tp] - siz[u], dp[u]);
	if (dp[u] <= (siz[tp] / 2)) {
		ans += u;
	}
}

void solve() {
	n = read<int>();
	int x, y;
	rep (i, 1, n - 1, 1) {
		x = read<int>(), y = read<int>();
		e[x].emplace_back(y);
		e[y].emplace_back(x);
		E.emplace_back(x, y);
	}
	for (tii it : E) {
		tie(limx, limy) = it;
		dfs(limx, 0);
		dfs(limy, 0);
		Dp(limx, 0, limx);
		Dp(limy, 0, limy);
	}
	cout << ans << '\n';
}

int main() {
	T = read<int>();
	while (T --) {
		init();
		solve();
	}
    return 0;
}

posted @ 2023-09-22 20:28 yi_fan0305 阅读(28) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

Loading

朝气蓬勃 后生可畏

四叶草少年，你将何去何从？

「解题报告」CSP - S 2019

[CSP-S2019] 格雷码

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

样例 #3

样例输入 #3

样例输出 #3

提示

[CSP-S2019] 括号树

题目背景

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

[CSP-S2019] 树上的数

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

[CSP-S2019] Emiya 家今天的饭

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

样例 #3

样例输入 #3

样例输出 #3

提示

[CSP-S2019] 划分

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

样例 #3

样例输入 #3

样例输出 #3

提示

[CSP-S2019] 树的重心

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

公告

朝气蓬勃后生可畏