【密码学】CBC反转字节攻击
前言
暑假刷安全牛的课,看视频有点够了,想做点题,选择了实验吧,结果上来就整懵了
web题,牵扯到了CBC反转字节攻击,密码学!?
查阅资料,学习一下
CBC加解密
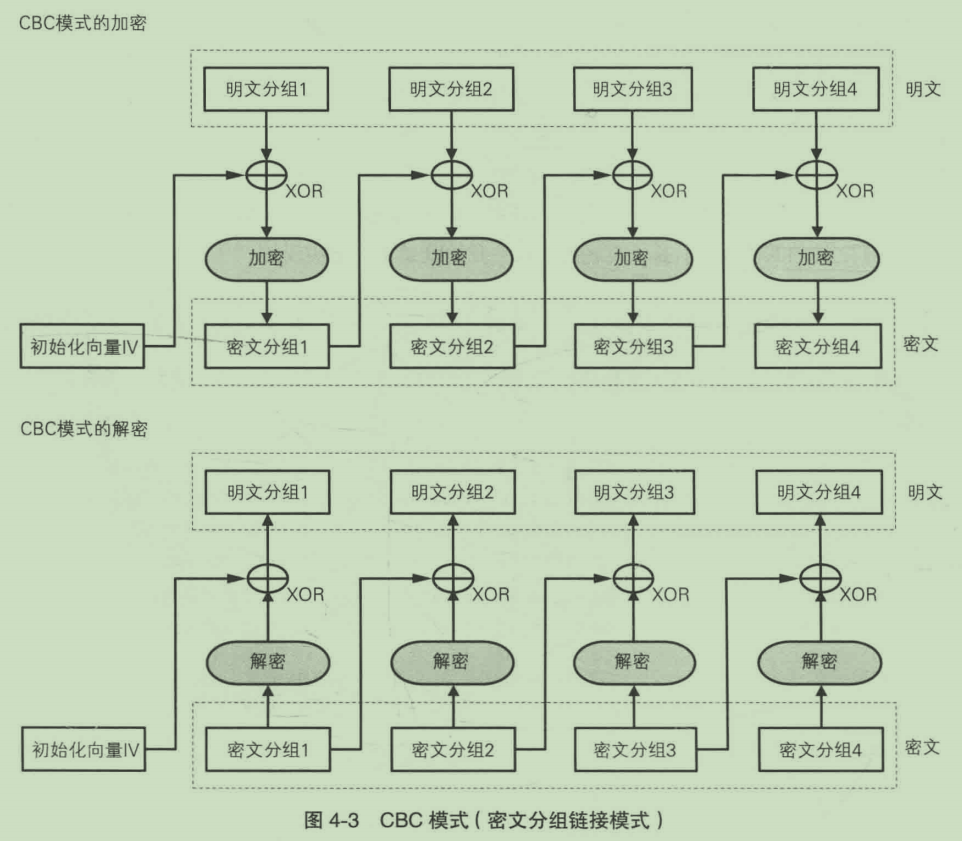
CBC 模式中会先将明文分组与前一个密文分组进行 XOR 运算,然后再进行加密。
当然,对第一个明文分组来说,是没有前一个密文分组的,那么就需要一个初始化向量(简称IV)
CBC加解密图示:
异或的概念
当两个数的二进制表示进行异或运算时,当前位的两个二进制表示不同则为 1,相同则为 0。该方法被广泛推广用来统计一个数的 1 的位数
参与运算的两个值,如果两个相应 bit 位相同,则结果为 0,否则为 1。
即:
0 ^ 0 = 01 ^ 0 = 10 ^ 1 = 11 ^ 1 = 0
按位异或的 3 个特点:
(1) 0 ^ 0 = 0,0 ^ 1 = 1 即 0 异或任何数=任何数
(2) 1 ^ 0 = 1,1 ^ 1 = 0 即 1 异或任何数 = 任何数取反
(3) 任何数异或自己=把自己置 0
CBC反转字节攻击
精髓
通过损坏密文字节来改变明文字节
讲解
根据解密方式我们可以知道,A=密文分组2,B=明文分组3,C为经过解密但还没进行异或的密文分组3,D为我们经过攻击反转要得到的明文。
在整个过程中,明文、密文我们都是知道的,但是加解密的密钥是不知道的,所以我们不能直接改变信息,要通过下面的方法进行反转字节攻击
方便查看:A = 密文分组 2,B = 明文分组 3,C 为经过解密但还没进行异或的密文分组 3(就简称为密文分组 3 了),D 为我们经过攻击反转要得到的明文。
B = A ^ C(解密时)解释:明文分组 3 = 密文分组 2 ^ 解密后的密文分组 3(解密时)
C = A ^ B(加密时)解释: 密文分组 3 = 密文分组 2 ^ 明文分组 3(加密时)
那么发现:
B ^ A ^ C = 0
解释:明文分组 3 ^ 密文分组 2 ^ 密文分组 3 = 密文分组 3 ^ 密文分组 3 = 0
此时如果:
A ^ B ^ C ^ D = D
解释:明文分组 3 ^ 密文分组 2 ^ 密文分组 3 ^ 任意值 = 密文分组 3 ^ 密文分组 3 ^ 任意值 = 0 ^ 任意值 = 任意值
也就是说我们如果改变了密文为 A = A ^ B ^ D,就可以使解密后的明文成为:D
总结
公式可以总结为下:原本的密文改为:原本的密文 ^ 原本对应的明文 ^ 希望变成的值


 浙公网安备 33010602011771号
浙公网安备 33010602011771号