数据结构学习笔记(四)--顺序表
数据结构学习笔记(四)--顺序表
顺序表是用顺序存储方式实现的线性表。
点击进入上一篇:数据结构学习笔记(三)--线性表的定义和基本操作
顺序表的定义
顺序表 --用顺序存储的方式实现的线性表
什么是顺序存储
顺序存储:把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中,元素之间的关系由存储单元的邻接关系来体现。
图形表示
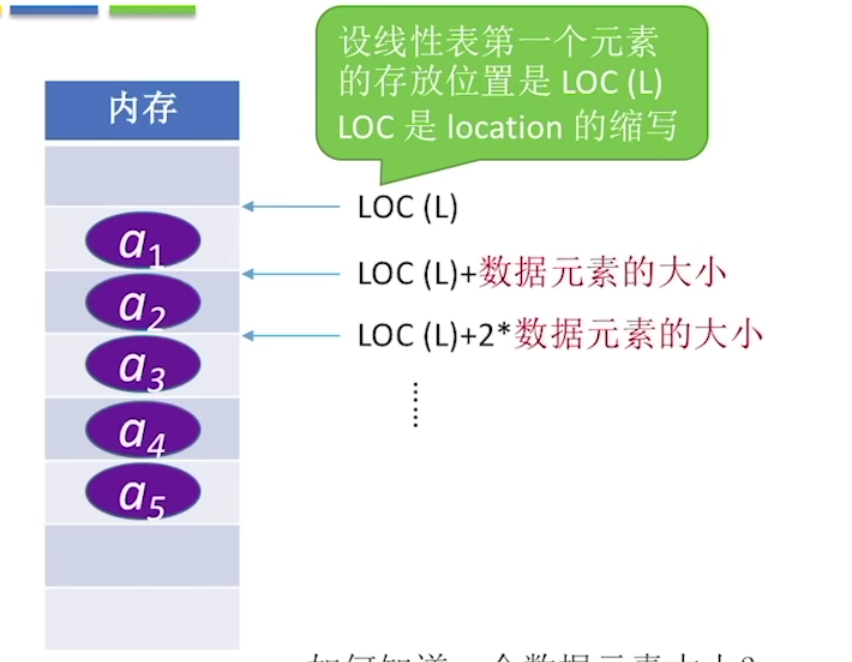
顺序表的实现方式
静态分配
定义一个静态数组存放数据元素。
代码实现
用c语言举例:
#include <stdio.h>
#define MaxSize 10 //定义最大长度
typedef struct{
int data[MaxSize]; //用静态的“数组”存放数据元素
int length; //顺序表的当前长度
} SqList; //顺序表的类型定义(静态分配方式),自定义命名
//基本操作 ——初始化一个顺序表
void InitList(SqList &L){
for(int i=0;i<MaxSize;i++)
L.data[i] = 0; //将所有数据元素设置为默认初始值
L.length = 0; //顺序表初始长度为0
}
注:如果没有初始化数据结构,直接打印顺序表,打印出来的数据未知(内存中的遗留数据,也称脏数据)
静态分配的特性
顺序表的表长开始确定后无法更改(存储空间是静态的)
动态分配
使用指针相关知识和c语言malloc、free函数动态申请和释放内存空间。
代码实现
用c语言举例:
#include <stdlib.h>
#define InitSize 10 //默认的最大长度
typedef struct{
int *data; //指示动态分配数组的指针
int MaxSize; //顺序表的最大容量
int length; //顺序表的当前长度
} SeqList;
//基本操作 ——初始化一个顺序表
void InitList(SeqList &L){
//用malloc函数申请一片连续的存储空间
L.data = (int *)malloc(InitSize * sizeof(int)); //注意类型转换
L.length = 0;
L.MaxSize = InitSize; //初始化顺序表最大长度
}
//基本操作 ——增加动态数组的长度
void IncreaseSize(SeqList &L,int len){
int *p = L.data; //创建一个指针将指向原data数据所在内存,类似于一个temp;
L.data = (int *)malloc((L.MaxSize+len)*sizeof(int));//给data分配一个新的,增大后的内存空间
//遍历将原来的数据赋值给新的地址(时间开销大)
for(int i=0;i<L.length;i++){
L.data[i] = p[i]; //将原data数据赋值给新的data
}
L.MaxSize = L.MaxSize +Len; //顺序表最大长度增加 len,重新定义顺序表最大长度
free(p); //释放原来的内存空间
}
顺序表的特点
- 随机访问,即可以在O(1)时间内找到第i个元素。
- 存储密度高,每个节点只存储数据元素。
- 拓展容量不方便(即便采用动态分配的方式实现,拓展长度的时间复杂度也比较高)。
- 插入、删除操作不方便,需要移动大量元素。
顺序表的基本操作
顺序表的初始化
见顺序表的实现方式中的代码示例
顺序表的插入
ListInsert(&L,i,e):插入操作。在表中第i个位置上插入指定元素e。
代码实现
采用静态分配的存储方式,用c语言举例:
bool ListInsert(SqList &L,int i,int e){
//首先判断参数是否合理,保持代码的健壮性
if(i<1 || i>L.length+1) //判断i的范围是否有效
return false;
if(L.length>=MaxSize)
return false;
for(int j=L.length;j>=1;j--) //将第i个元素及之后的元素后移
L.data[j] = L.data[j-1];
L.data[i-1] = e; //在指定位置i处放入e。(因为线性表是位序从1开始,代码数组下标从0开始,故为i-1)
L.length++; //长度加1
return true;
}
插入操作的时间复杂度
- 最好情况:新元素插入到表尾,不需要移动元素,i = n+1,循环0次;最好时间复杂度 = O(1)
- 最坏情况:新元素插入到表头,需要将原有的n 个元素全部向后移动,i = 1,循环n次;最坏时间复杂度 = O(n)
- 平均情况:假设新元素插入到任何一个位置的概率相同,即i = 1,2,3, ... ,length+1 的概率都是 p = 1/(n+1),计算构成等差数列求得,T(n) = n/2;平均时间复杂度 = O(n)
顺序表的删除
ListDelete(&L,i,&e):删除指定位序上的元素,并用e带回删除数据的值。
代码实现
采用静态分配的存储方式,用c语言举例:
bool ListDelete(SqList &L,int i,int &e){
if(i<1 || i>L.length) //判断i的范围是否有效
return false;
e = L.data[i-1]; //将被删除的元素赋值给e
for(int j=i;j<L.length;j++) //将第i个位置后的元素前移
L.data[j-1]=L.data[j];
L.length--; //线性表长度-1
return true;
}
删除操作的时间复杂度
- 最好情况:删除表尾元素,不需要移动其他元素,i = n,循环0次;最好时间复杂度 = O(1)
- 最坏情况:删除表头元素,需要将后续的n-1个元素全部向前移动,i = 1,循环 n-1次;最坏时间复杂度 = O(n)
- 平均情况:假设删除任何一个元素的概率相同,即i = 1,2,3, ... ,length 的概率都是 p = 1/n,计算构成等差数列求得,T(n) = (n-1)/2;平均时间复杂度 = O(n)
注意事项
删除位序为i的元素和删除数组下标为i的元素并不相同,前者从1开始,后者从0开始。
顺序表的查找
按位查找
GetElem(L,i):按照顺序表位序查找数据的值,并返回数据的值。
代码实现
采用静态分配的存储方式,用c语言举例:
int GetElem(SqList L,int i){
return L.data[i-1]; //直接返回该位序所在数组下标的值
}
注:因调用malloc函数的内存分配和定义数组的内存分配方式相似,故动态分配与静态分配的按位查找都是如此,以查询数组下标的形式实现。
时间复杂度
按位查找的时间复杂度:O(1) (体现顺序表“随机存取”的特性)
按值查找
LocateElem(L,e):在表中查找具有给定关键字值的元素,并返回其位序
代码实现
采用静态分配的存储方式(当然,动态也是这么做),用c语言举例:
int LocateElem(SqList L,int e){
for(int i=0;i<L.length;i++){
if(L.data[i]==e)
return i+1; //数组下标为i的元素值等于e,返回其位序i+1
}
return 0; //循环结束还没找到,说明查找失败
}
时间复杂度
- 最好情况:目标元素在表头,循环1次;最好时间复杂度 = O(1)
- 最坏情况:目标元素在表尾,循环n次;最坏时间复杂度 = O(n)
- 平均情况:假设目标元素出现在任何一个位置的概率相同,都是1/n,平均循环次数 = (n+1)/2,平均时间复杂度 = O(n)
注意事项
《数据结构》考研初试中,手写代码可以直接用 “==”,无论e的数据类型是基本数据类型还是结构类型。
手写代码主要考察学生是否能理解算法思想,不会严格要求代码完全可运行。
但如果有的学校考《C语言程序设计》,那么对语法要求就会更加严格。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号