P1 方程组的几何解释
http://bilibili.com/video/BV1Gb411g7Cd?p=2&spm_id_from=pageDriver
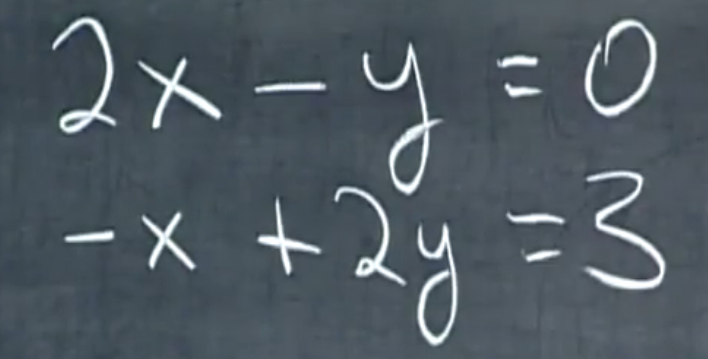

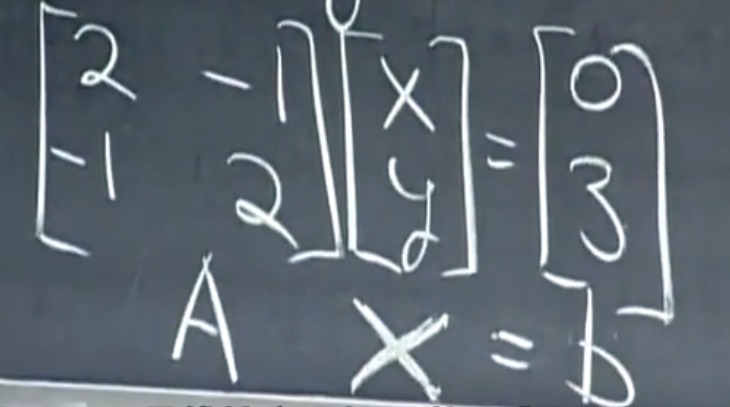

注解:
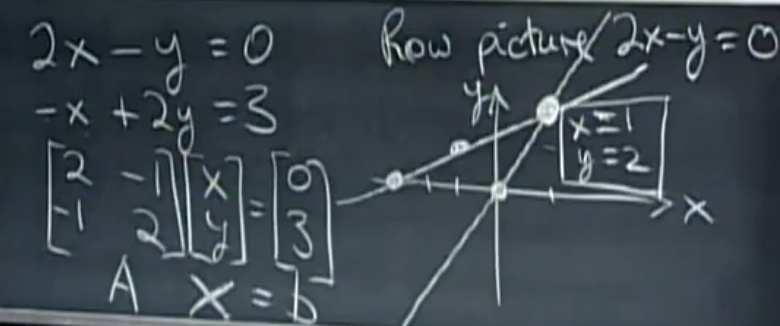
- Row Picture就是行图像的意思。
- 行图像是两条直线,方程组的解是两条直线的交点(1,2).
- 重要的是列图像。
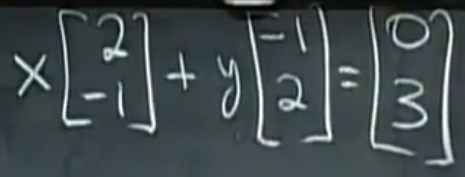
注解:
- 找到一个线性组合,使得两个列向量的线性组合是另一个向量。

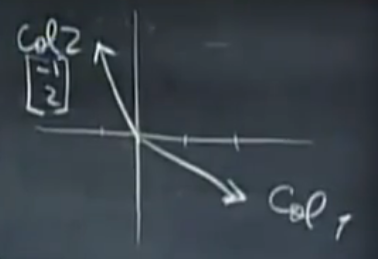
注解:
- 此图画出了列向量[-1,2]和列向量[2,-1]
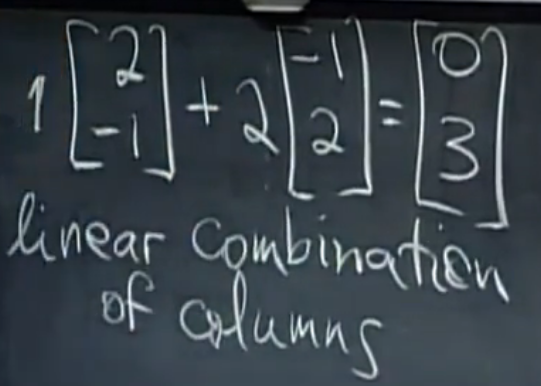
注解:
- 正确的线性组合是:1个[2,-1]和2个[-1,2]
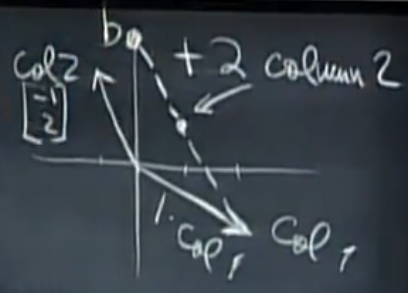
注解:
- 这样的线性组合就能得到b向量。

注解:
- 此时,很自然的会思考,那两个列向量的所有的线性组合是什么?

上面是2个方程2个未知数,系数矩阵是2*2的例子,也是就2维平面中的例子,下面看下3个方程3个未知数,系数矩阵是3*3的情况,也即是空间中的情况。



- 用矩阵表示可以使得方程组看起来更加的简洁。
首先用行作图的方法解方程组。
首先画出方程-x+2y-z=-1在3维空间中所表示的平面。这个平面内点是满足方程-x+2y-z=-1的所有点。
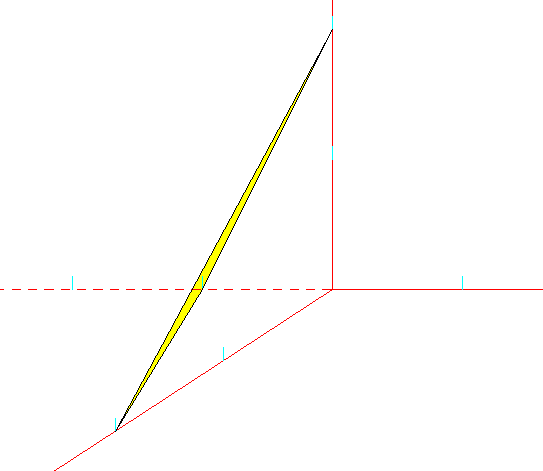
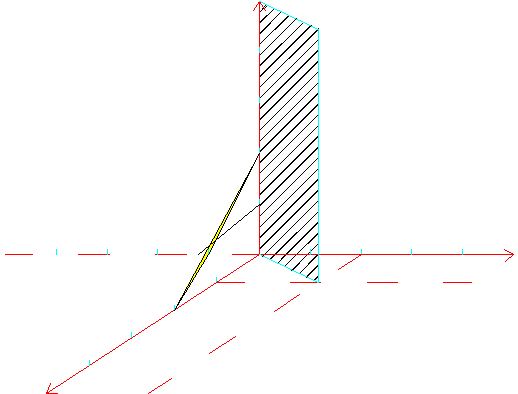
用matlab代码可视化方程组的解(3个平面交于一点的解):
[x z] = meshgrid([0:0.1:pi]); y = 2*x; mesh(x,y,z,'FaceColor','r','EdgeColor','none'); % 绘制曲面 y=2*x xlabel('x');ylabel('y');zlabel('z');alpha(0.5); x = 2*y - z+1; hold on; mesh(x,y,z,'FaceColor','g','EdgeColor','none'); % 绘制曲面 x = 2*y - z+1 xlabel('x');ylabel('y');zlabel('z');alpha(0.5); z = (3*y+4)/4; mesh(x,y,z,'FaceColor','b','EdgeColor','none'); % 绘制曲面 z=0 alpha(0.5);
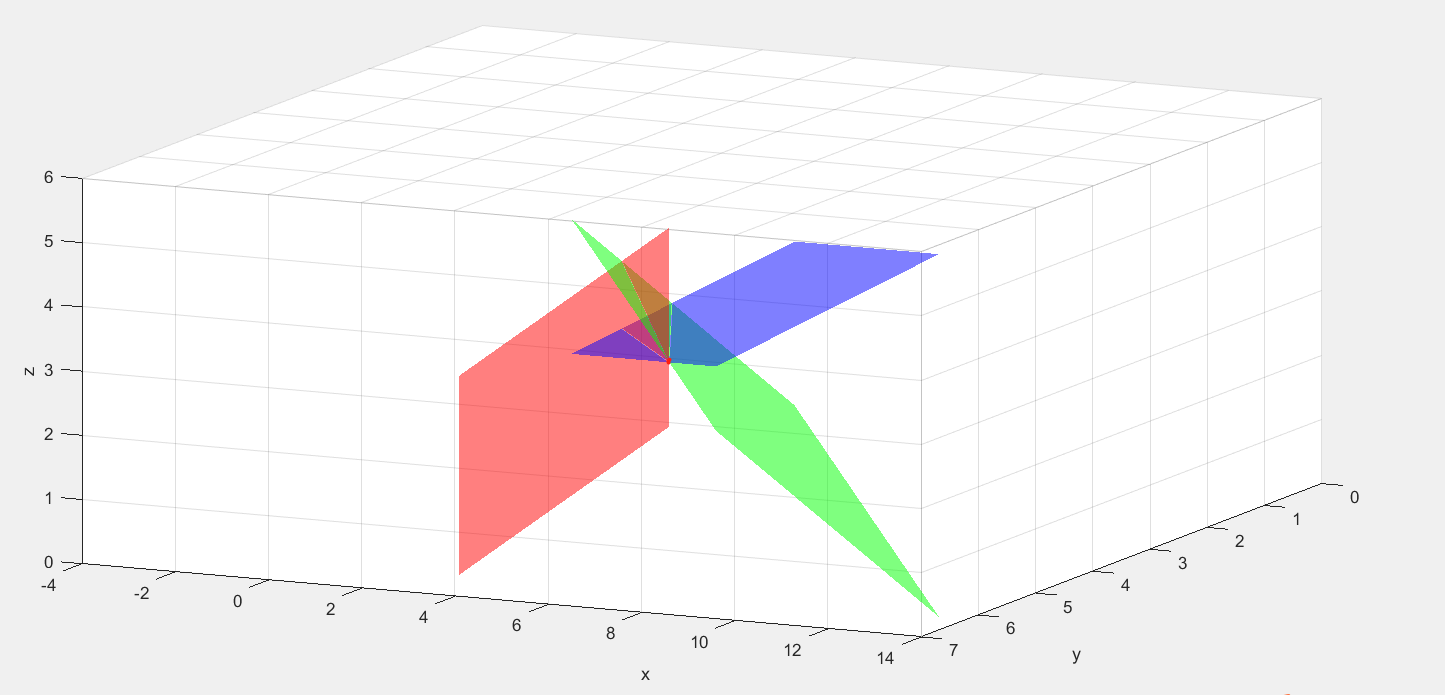

下面按照列图像理解方程组的几何意义。

即:对于3个3维列向量而言,什么样的线性组合能够把左边的3个向量组合成右边的那个向量。
注意:
- 向量组中向量的维数等于方程组的数量。
- 向量组中向量的维数就是空间的维数。向量是3维的,空间就是3维的。
- 向量组中列向量的个数等于未知数的个数。
- 显然,解是[0,0,1].这就是行图像中难以看出的交点。

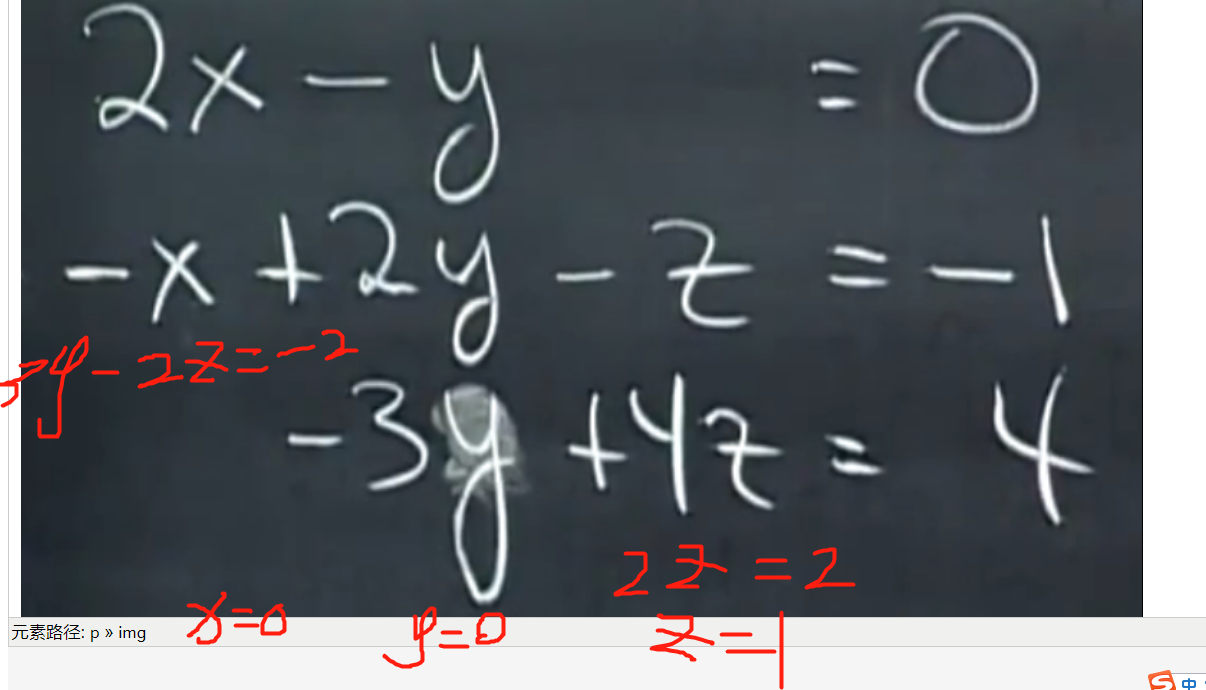
首先手工解出方程组的解,组合方式是[0,0,1]
利用matlab代码绘制出3个向量:
clear;clc;close all; O=[0,0,0]; A=[2,-1,0]; B=[-1,2,-3]; C=[0, -1,4]; %A=[4,5,6]; %B=[-10,6,7]; %C=[-1 ,8,0]; scale=1; %quiver3(A(1),A(2),A(3),B(1)-A(1),B(2)-A(2),B(3)-A(3),scale);%表示以A为起点,由A指向B text(A(1),A(2),A(3),'A');%在A点附件标注字母A %axis([-10 4 5 8 0 7]);xlabel('x');ylabel('y');zlabel('z');%规范x,y,z坐标轴刻度范围,及在各自坐标轴上标注字母x,y,z axis([-1 2 -1 2 -3 4]);xlabel('x');ylabel('y');zlabel('z');%规范x(-10,4),y(5,8),z(0,7)坐标轴刻度范围,及在各自坐标轴上标注字母x,y,z grid on;%绘网格 hold on; %quiver3(B(1),B(2),B(3),C(1)-B(1),C(2)-B(2),C(3)-B(3),scale); text(B(1)-0.3,B(2),B(3),'B'); hold on; %quiver3(A(1),A(2),A(3),C(1)-A(1),C(2)-A(2),C(3)-A(3),scale); text(C(1),C(2),C(3)-0.5,'C'); hold on; text(O(1),O(2),O(3)-0.2,'O'); quiver3(O(1),O(2),O(3),C(1)-O(1),C(2)-O(2),C(3)-O(3),scale); quiver3(O(1),O(2),O(3),B(1)-O(1),B(2)-O(2),B(3)-O(3),scale); quiver3(O(1),O(2),O(3),A(1)-O(1),A(2)-O(2),A(3)-O(3),scale);
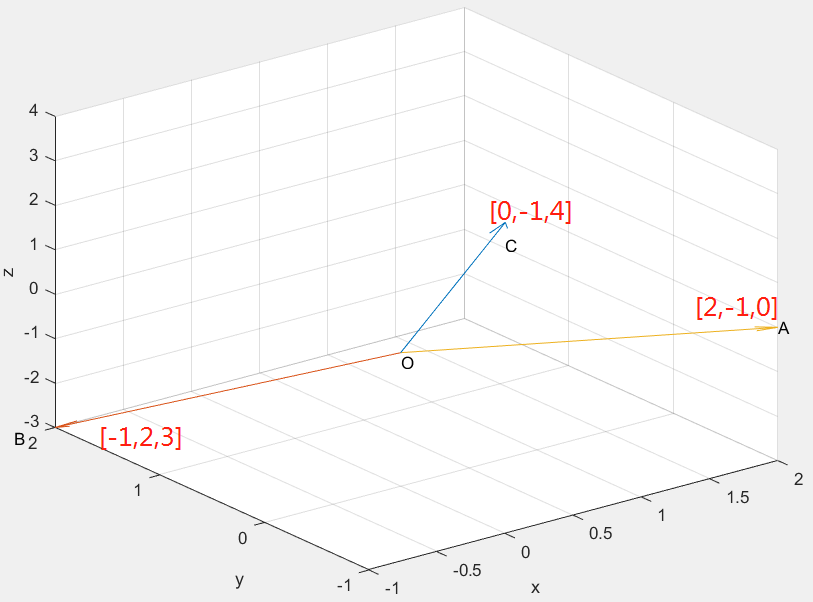

[0,0,1].
A=
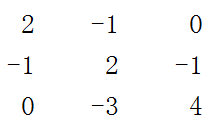
AX=b
X=[x,y,z]T
假如b是[1,1,-3],那么解显然是X=[1,1,0]T
在保证系数矩阵不变的的情况下,不同的线性组合形成了3维空间中的任一向量。

![]()
![]()
![]()
以上4个问题都是问的这样一个问题:是否存在这样的线性组合(x,y,z组合)?

![]()
![]()
![]()
什么时候3个列向量无法通过(任意一种线性)组合得到b?
![]()
![]()
![]()







9维空间无法具象,






取决于这9个列向量是否是相关的。








如果9个列向量中,第9个列向量正好等于第8个列向量的话,那么这9个列向量


有些事情,





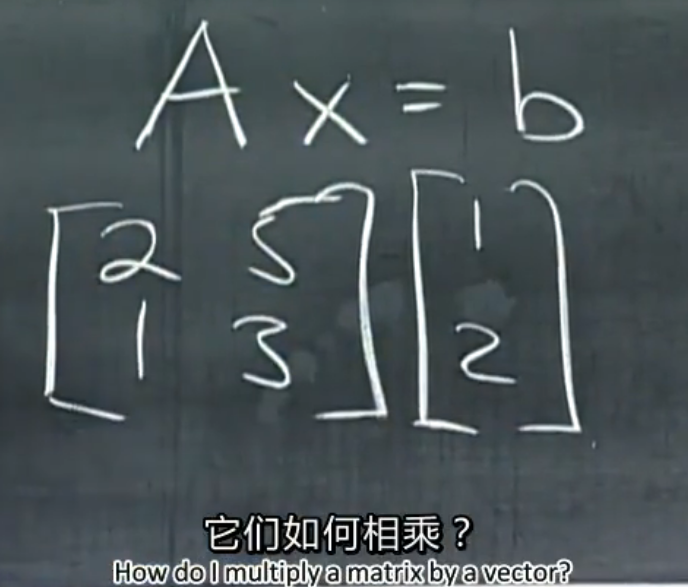
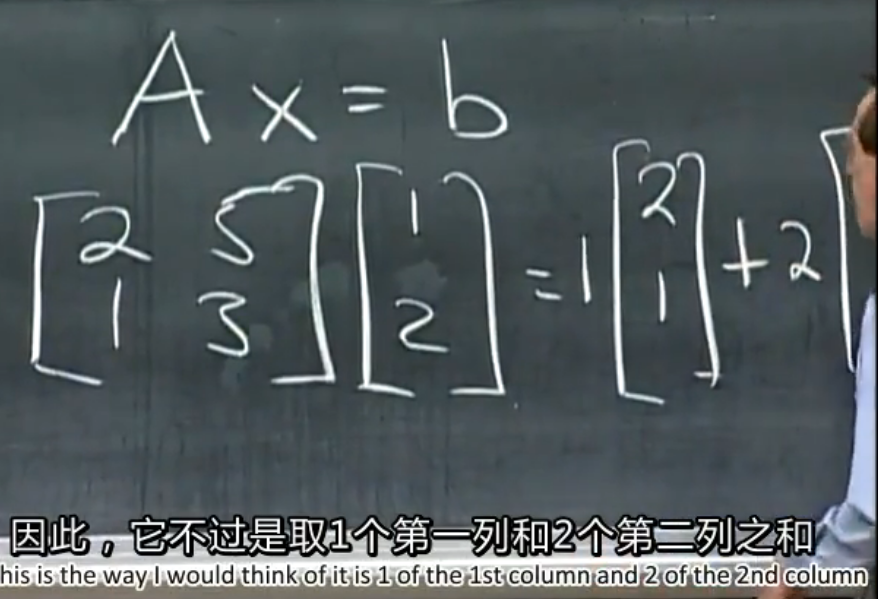
这个是讲者最喜欢的矩阵乘以向量的乘法的方法。

另一种常用的方法是,矩阵A的每一行分别和X点乘。



小结:
- 不是一上来就讲行列式,而是从方程组引入矩阵。
- 对方程组进行几何解释,让人从直观上了解到方程组的解就是系数矩阵的列向量的线性组合。
- 矩阵能让一个向量映射成另一个向量。
- 在3维中,对于一个矩阵的列向量而言,它们不同的线性组合可以得到整个3维空间。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号