线段树略解(20191028更新)
@
写在前面
线段树是提高组非常非常重要的东西,是考纲唯一一个数据结构(树状数组除外),它的重要性不言而喻。本文为备考的我,也为同样备考的你整理了线段树的知识点,力求详细,并将持续更新。如果你有什么好点子,欢迎评论。
线段树
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
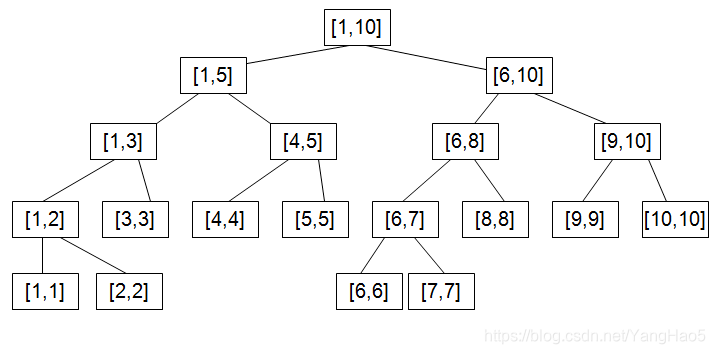
如上图所示的线段树维护 \([1,10]\) 区间。每个节点上的区间表示该节点维护的区间。
线段树的时间复杂度 \(O(\log N)\)(建树复杂度为 \(O(N)\)),空间复杂度 \(T(N)\)。
单点修改操作
从根节点开始,选择涵盖目标节点的儿子往下跳,直到找到目标节点。修改数值,回溯更新数值。
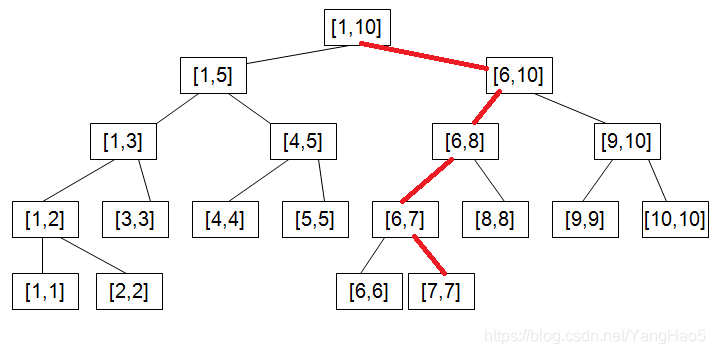
如图所示,红色路径是更新 7 号节点的路径图。
区间查询操作
设节点 \(x\) 维护的区间是 \([x.l,x.r]\),左儿子、右儿子分别是 \(x.ls,x.rs\)。
不难发现,当询问区间恰好为 \([x.l,x.r]\) 时,答案即为 \(x.d\)。
那如果不是呢?使用分治思想,将这个任务传给 \(x\) 的两个儿子,再从儿子那里接受答案。重复以上操作,直到询问被回答。
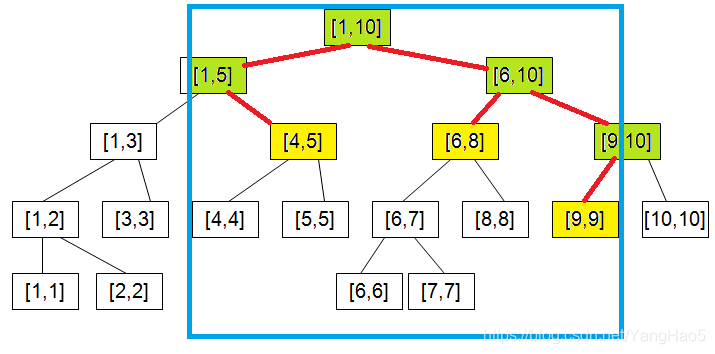
举个例子。假设我们询问 \([4,9]\) 这个区间。
我们现在在 \([1,10]\),发现这个问题需要左儿子和右儿子一起帮忙才能回答,所以访问两个儿子。
对于 \([1,5]\),发现右儿子就是答案的一部分,返回右儿子的 \(d\);
对于 \([6,10]\),左儿子和右儿子一起帮忙;
对于 \([6,8]\),发现该点就是答案的一部分,返回该点的 \(d\);
对于 \([9,10]\),发现左儿子是答案的一部分,返回左儿子的 \(d\)。
这个问题就这样被回答了。
如上图所示,绿色的点表示需要遍历儿子才能回答问题;黄色的节点表示直接返回该点数值;红色边是经过的边。
至此,我们已经学会使用线段树解决 单点修改、区间查询 问题了。
区间修改、单点查询问题
例题 1 您需要写一个数据结构,维护一个序列 \(a\),支持以下操作:
- 将 \(a[l],a[l+1],...,a[r]\) 的值加 \(d\);
- 查询 \(a[x]\) 的值。
考虑将此类问题转化成我们已经学会的“单点修改、区间查询问题”。
我们发现,给一区间内的所有数加 \(d\) 时,区间内相邻两数之差不变。所以区间加一个数等价于 修改边界处的差。
设 \(c[i]=a[i]-a[i-1],a[0]=0\),不难发现$$a[x]=\sum_{i=1}^{x}{c[i]}$$
所以,查询一个数 \(a[x]\) 就被转化成求 \(c\) 数组的前缀和(连续的)。
那如果是区间修改、区间查询呢?
区间修改操作
回顾区间查询的过程。

总结发现,优化时间复杂度的方法是 不走到叶子节点,在非叶节点结束本次查询。
不妨尝试在区间修改中应用这个策略。与查询类似,我们给每个点设置一个值 \(lazy\),表示这个节点维护的区间的每个点共有的数值。比如,给 \([1,10]\) 里的每个数加上 \(d\),那么我们可以给 \([1,10]\) 这个点的 \(lazy\) 加 \(10\)。
查询时,如果该节点是绿色的,则将他的 \(lazy\) 值下发给他的儿子。就像这样:
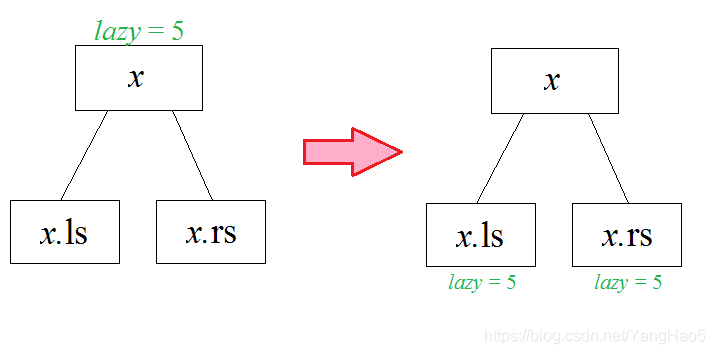
如果该节点是黄色的,直接累加 \(lazy\) 对答案的贡献,也就是 \(lazy\times(r-l+1)\)。
例题与练习
我们已经粗略介绍了线段树的基本操作。下面我们来看几道例题。
例题 2 已知一个数列,你需要进行下面两种操作:
- 将某区间每一个数加上 \(x\);
- 求出某区间每一个数的和。
区间修改、区间查询的线段树。
例题 3
一棵树上有 \(n\) 个节点,编号分别为 \(1\) 到 \(n\),每个节点都有一个权值 \(w\)。
我们将以下面的形式来要求你对这棵树完成一些操作:
I. CHANGE u t :把结点 \(u\) 的权值改为 \(t\);
II. QMAX u v:询问从点 \(u\) 到点 \(v\) 的路径上的节点的最大权值;
III. QSUM u v:询问从点 \(u\) 到点 \(v\) 的路径上的节点的权值和。
先把这棵树按 \(dfs\) 序排列,拍成一个序列。这样,我们便发现:树上两点的路径在序列上是若干段的连续序列。
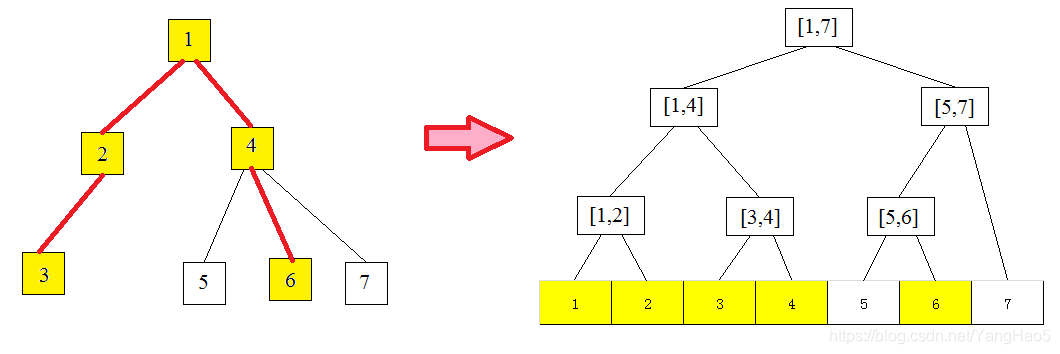
使用树链剖分 + 线段树维护即可。
例题 4 请求你维护一个数列,要求提供以下两种操作:
- 查询当前数列中末尾 \(L\) 个数中的最大的数,并输出这个数的值。
- 将 \(n\) 加上 \(t\),其中 \(t\) 是最近一次查询操作的答案(如果还未执行过查询操作,则 \(t=0\)),并将所得结果对一个固定的常数 \(D\) 取模,将所得答案插入到数列的末尾。
记录一下现在队列的长度即可。详见这儿。
练习 1 (luogu P1168 中位数)给你 \(N\) 个数 \(a[1...N]\),求 \(a[1...1],a[1...3],a[1...5],...,a[1...N]\) 的中位数。
备注: 用 vector + upper_bound 亦可。
练习 2 (luogu P1382 楼房)\(x\) 轴上有 \(n\) 个矩形,用三个整数 \(h[i],l[i],r[i]\) 来表示第i个矩形:矩形左下角为 \((l[i],0)\),右上角为 \((r[i],h[i])\)。在轮廓线长度最小的前提下,从左到右输出轮廓线。
练习 3 (luogu P1442 铁球落地)\(n(n≤10^5)\) 个平台上空有一个铁球,球每次落到某个平台上后,游戏者可以选择向左或向右滚,球滚动和落下的速度都是 \(1\)。由于铁球的质量不太好,每次落下的高度不能超过 \(MAX\)。设计一种策略,使得球尽快落到地面而不被摔碎。假设地面高度为 \(0\),且无限宽。
二维线段树
顾名思义,就是将原本在一位数组上的线段树拓展到二维平面上。先看一道例题。
例题 5 您需要写一种数据结构,维护一个矩阵 \(A[1...N][1...M]\),支持以下操作:
1 x_1 y_1 x_2 y_2 d将子矩阵 \(A[x_1][y_1]...A[x_2][y_2]\) 的每个数的值加 \(d\);2 x_1 y_1 x_2 y_2查询子矩阵 \(A[x_1][y_1]...A[x_2][y_2]\) 的每个数的和。
设操作数为 \(K\),则有 \(1\leq N,M\leq10^4,1\leq K\leq 10^5\)。
Solution
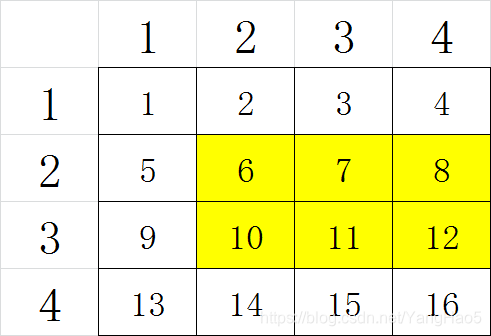
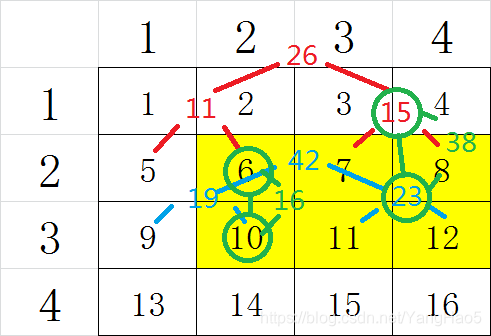
我们以上图为例介绍二维线段树,黄色矩形是查询区间。
一种很显然的想法是,将每行的 \(M\) 个数建一棵线段树,然后每行统计答案后相加(此处未画出第 1 行和第 4 行的线段树):
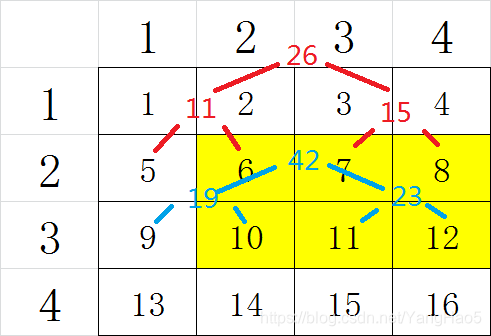
不难发现,以此法建好线段树后,每行查询的列数的区间完全一样,而且查询的点在树上的相对位置一一对应:
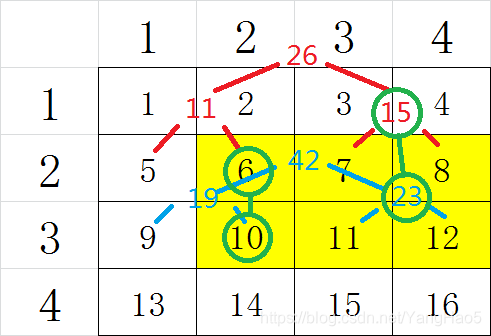
就像上图一样,每条用绿色线连接的绿色点在树上的相对位置是相同的。
不妨用线段树维护每条绿线上的数,这样我们就不需要循环遍历每一行了。
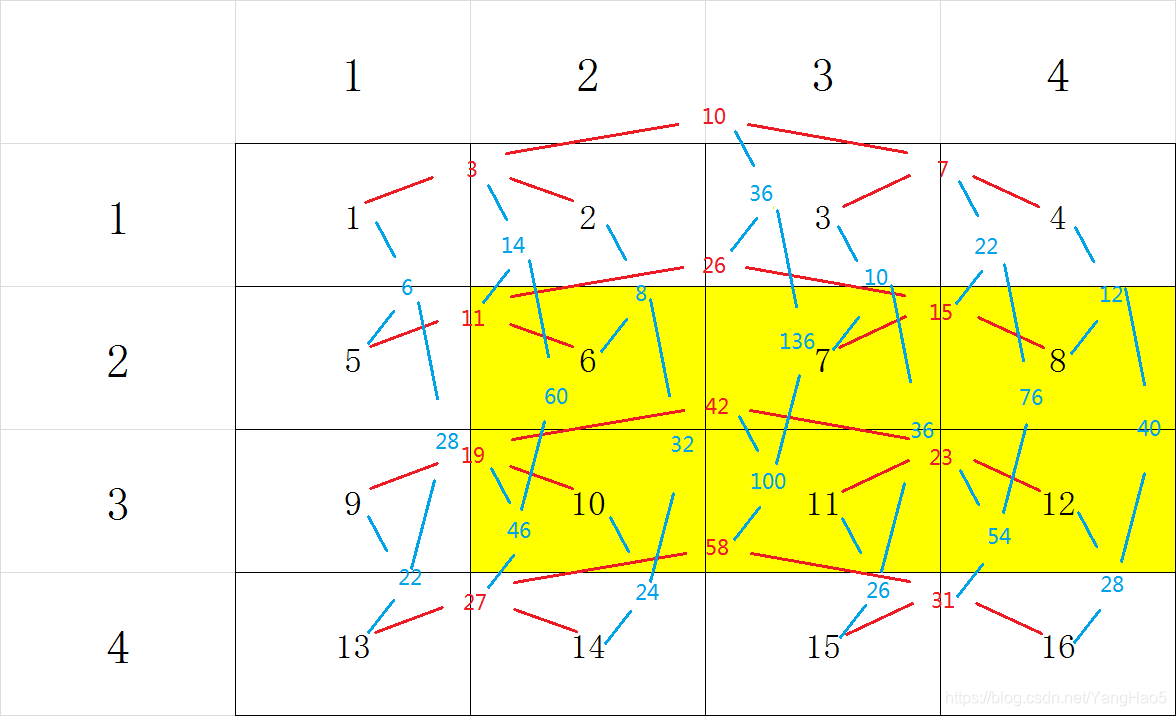
完整的图片如下:
(这里插一句,制图不易,转载请注明出处。谢谢!)
时间复杂度 \(O(K\log N\log M)\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号