《FFT家族—从不会到崩溃(坑)》读blog笔记
免责声明
原文地址https://blog.csdn.net/linjiayang2016/article/details/80341958,作者
本文是对原文的微薄补充,目的是为了更好地读懂原文。
正弦, 余弦
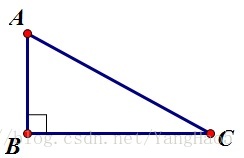
$RT.\ Rt△ABC∠B=90°$,则有
快速傅里叶变换过程
以用解决多项式乘法的问题为例。
$1.\ a,b$;
$2.\ a,b$分别做傅里叶变换;
;
$4.\ an$.
## 关于单位根的补充说明 $\ \ \ \ w^k_n*w^1_n$ $=(\cos\ k*\frac{2\pi}{n}+\sin\ k*\frac{2\pi}{n}\ i)\ *\ (\cos\ \frac{2\pi}{n}+\sin\ \frac{2\pi}{n}\ i)$ $=\cos\ k*\frac{2\pi}{n}\ *\ \cos\ \frac{2\pi}{n}\ +\ \sin\ k*\frac{2\pi}{n}\ i\ *\ \cos\ \frac{2\pi}{n}$ $\quad+\ \cos\ k*\frac{2\pi}{n}\ *\ \sin\ \frac{2\pi}{n}\ i\ +\ \sin\ k*\frac{2\pi}{n}\ i\ *\ \sin\ \frac{2\pi}{n}\ i$ $=\cos\ ((k+1)*\frac{2\pi}{n})\ +\ \sin\ ((k+1)*\frac{2\pi}{n})$ $=w^{k+1}_n.$
## 两角和公式 $\sin\ (A+B)=\sin\ A·\cos\ B+\cos\ A·\sin\ B$ $\cos\ (A+B)=\cos\ A·\cos B-\sin\ A·\sin\ B$
## 快速傅里叶逆变换 原文中的$y$指的是上文的$a$,原文中的$a$指答案数组.
对于$c_i=\sum\limits^{n-1}_{j=0}a_j(\sum\limits^{n-1}_{i=0}(w^{j-k}_n)^i)$$\ \ \ (k$是常数$)$, $1.\ $当$j-k=0$时,$w^{j-k}_n=1+0i$,$\therefore \sum\limits^{n-1}_{i=0}(w^{j-k}_n)^i=n$; $2.\ $当$j-k≠0$时,原文已阐述详尽,在此不做赘述.
## 线性求翻转序列 对于已知的翻转序列$r_i$,我们在它前面加上$1$或$0$,就得到了$r_{2i+1}$和$r_{2i+2}.$ 举例. $\because r_6=11_{(2)}$, $\therefore r_{13}=$ `0`$11_{(2)}.\ \ $(在$r_6$前补`0`) $\quad r_{14}=$ `1`$11_{(2)}.\ \ $(在$r_6$前补`1`)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号