C++ set 用法略解（20191031更新）

@

目录

• 初步用法讲解
• 进阶用法讲解
• 注意事项
• 例题
• 练习

初步用法讲解

先看一段代码。

#include<iostream>
#include<set>
#include<cstdio>
#include<cstdlib>
#include<cstring>

using namespace std;

set<int> s;
int n;
int a;

int main(){
	cin>>n;
	for(int i=1;i<=n;++i){
		cin>>a;
		s.insert(a); 
	}
	for(set<int>::iterator it=s.begin();it!=s.end();++it)
		cout<<*it<<' ';	//flag
}

以上代码概括地介绍了 set 的部分语法。该程序运行结果如下图。

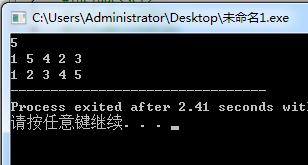
我们看到，set 内部是有序的，STL 提供了一种迭代器 iterator，用于遍历 set。

set 是一个平衡树，支持以下几种操作：

1. 插入一个元素；
2. 删除一个元素；
3. 查询一个元素的前驱、后继。

每次操作的时间复杂度 \(O(\log n)\)。

下表列出了 set 的部分常用函数。

函数名称	函数功能
begin()	返回 set 初始元素迭代地址
end()	返回 set 末尾元素迭代地址 +1
insert(type x)	插入元素 \(x\)
erase(type x)	删除元素 \(x\)
size()	返回 set 的元素个数
clear()	清空 set
empty()	判断 set 是否为空
find(type x)	返回元素 \(x\) 在 set 中的迭代器
count(type x)	返回元素 \(x\) 在 set 中的出现次数

进阶用法讲解

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<set>
#include<algorithm>

using namespace std;

set<int> s;
int n;
int a;

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i){
		scanf("%d",&a);
		s.insert(a);
	}
	scanf("%d",&n);
	for(int i=1;i<=n;++i){
		scanf("%d",&a);
		set<int>::iterator it=s.lower_bound(a);
		printf("%d\n",(*it));
	}
}

上段代码使用了函数 lower_bound()，他是什么意思呢？

lower_bound(type x) 函数用来返回 set 中大于等于 \(x\) 且最小的数的迭代器。如果set 中没有满足条件的数，返回 end()。

upper_bound(type x) 与他类似。他被用来返回 set 中 严格大于 \(x\) 且最小的数的迭代器。如果set 中没有满足条件的数，返回 end()。

注意事项

1. end() 返回的是末尾元素迭代地址 +1；
2. erase() 未能成功删除元素时对 set 不产生影响；
3. find() 未能成功找到元素时返回的是 end()；
4. lower_bound()、upper_bound() 未能找到元素时返回的是 end()；
5. 函数

bool function(){
	set<int> s;
	s.insert(10);s.insert(20);
	set<int>::iterator it=s.lower_bound(9);
	printf("%d\n",*it);--it;
	return bool(it==s.begin());
}

被调用后输出 10，返回值是 true。

例题

例题 您需要写一个数据结构，维护一个初始长度为空的序列，支持以下操作：

1. 将整数 \(x\) 加入序列；
2. 查询序列中小于等于 \(x\) 且最大的数，若没有则输出 brz is a pig；
3. 查询序列中大于等于 \(x\) 且最小的数，若没有则输出 brz is a pig。

参考代码 使用 1 个 set 维护序列，对于 1. 操作直接 insert()，对于 3. 操作 lower_bound()，2. 操作细节比较多，详见代码。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<set>
using namespace std;

set<int> s;
int n;
int sx,sy;
set<int>::iterator it;

set<int>::iterator find(int x){
	it=s.lower_bound(x);
	if((*it)==x) return it;
	else return (it==s.begin())?s.end():(--it);
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i){
		scanf("%d%d",&sx,&sy);
		switch(sx){
			case 1:
				s.insert(sy);
				break;
			case 2:
				it=find(sy);
				if(it==s.end()) puts("brz is a pig");
				else printf("%d\n",*it);
				break;
			case 3:
				it=s.lower_bound(sy);
				if(it==s.end()) puts("brz is a pig");
				else printf("%d\n",*it);
				break;
			default:
				break;
		}
	}
}

练习

练习 已知 Jim 有 \(n\) 个宝石，现在他将这 \(n\) 个宝石从 \(1\) 到 \(n\) 排开编号从 \(1\) 到 \(n\)。Jim 发现他所有的宝石中竟然有不少是完全相同的的，我们规定每个宝石都有一个特征值 \(a_i\)，当两个宝石特征值相等时认为两个宝石相同。Jim 发现两个相同的宝石离得越接近越明显。Jim 现在有 \(m\) 个问题，他想问你在编号 \(l\) 到 \(r\) 这一区间里的所有宝石中，两个相同宝石的最近距离是多少（两个宝石的距离是它们编号的绝对值之差）。\(1\leq n,m\leq 2\times10^5\)。