【读书笔记】排列研究-线性顺序

upd 2020-08-09 19:53 完成最初稿

目录

• descent和ascent定义
• 开胃菜
• 欧拉数\(A(n,k)\)的递归方程
• 欧拉数相关的其他方程
• 欧拉数的显式方程Explicit formula
• 插曲
  • 斯特林数和欧拉数
  • (无符号)第二类斯特林数的显式方程
• 欧拉数和生成函数
  • 欧拉多项式的定义
  • 欧拉多项式的显式方程
• 研究欧拉数-a master GF
• 观察欧拉数金字塔研究性质
  • 欧拉数金字塔长这样
  • 给出一些实序列的property的定义
  • 欧拉多项式的所有根都是实的

吐个槽，

一个排列的reverse是说\(p^r=p_np_{n-1}...p_1\)

一个排列的inverse是说圆分解，每个圆都反向

descent和ascent定义

在一个排列\(p\)中，

我们说下标\(i\)是一个descent如果\(p_i>p_{i+1}\)

我们说下标\(i\)是一个ascent如果\(p_i<p_{i+1}\)

我们说排列在下标\(i\) changes direction 如果\(p_{i-1}<p_i>p_{i+1}\)（\(p_i\)是peak）或者\(p_{i-1}>p_i<p_{i+1}\)(\(p_i\)是valley)

下标\(i\)是一个excedance如果\(p_i>i\)

descent构成的位置集叫做 the descent set of \(p\), 记作\(D(p)\)

\(D(p)\)的大小记作\(d(p)\)或者\(des(p)\)

欧拉数\(A(n,k)\)表示the number of n-permutations with k-1 descents

欧拉数\(A(n,k)\)也表示the number of n-permutations with k-1 excedance

\(G(n,k)\)表示【\(k\)个alternating runs的n-permutaiton】的数量

排列被\(k-1\)个下降位分隔为\(k\)个ascending runs，举例，The three ascending runs of p=2415367 are 24, 15, and 367.

排列有\(k\)个alternating runs,在\(k-1\)个位置changes direciton ,散点图上看就是，\(k\)段折线，举例，Permutation 3561247 has three alternating runs，6是peak,1是valley

开胃菜

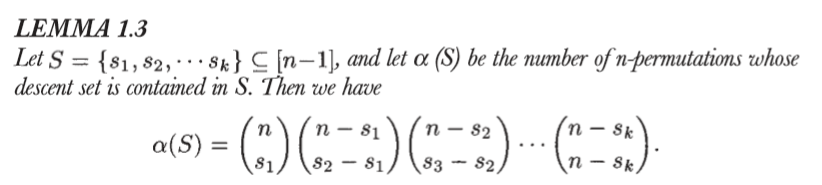
排旗公式，不解释

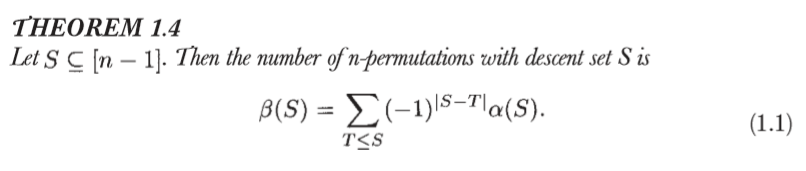
这种求和形式让人想到容斥原理

欧拉数\(A(n,k)\)的递归方程

upd 2021-04-04 今天检查发现好像写错了，可以看oeis给的递推方程

对所有满足\(k\leq n\)的正整数\(k\)和\(n\)

\[A(n, k+1)=(k+2) A(n-1, k+1)+(n-k-1) A(n-1, k) \]

给个证明

考虑从(n-1)-排列到k+1个descent的n-排列的转移，考虑\(n\)插入的位置

如果\(n\)插在最后或者插在【descent和descent后一位之间】，那么descent数目不变，那么要求转移前的(n-1)-排列有\(k+1\)个descent。
有\(k+1+(1)=k+2\)个选择，解释了右手边第一项

如果\(n\)插在其他位置，那么descent数目+1，那么要求转移前的(n-1)-排列有\(k\)个descent。
有\((n)-(k+1)=n-k-1\)个选择，解释了右手边第二项

吐个槽，这里书里给的方程错了，证明思路是对的

欧拉数相关的其他方程

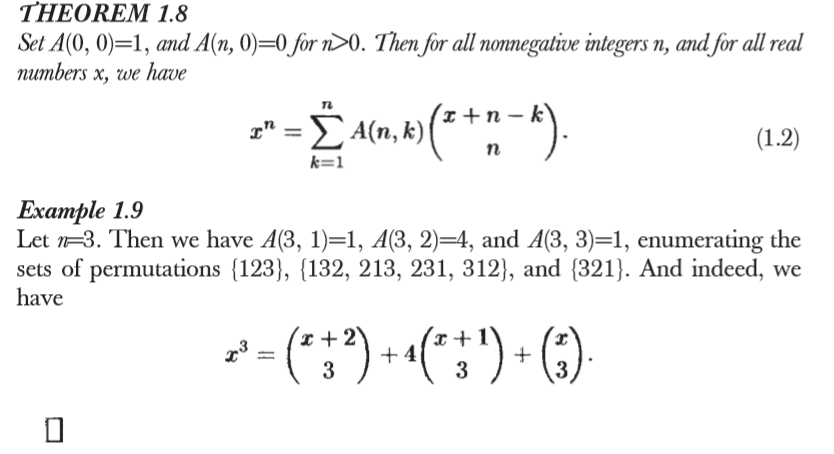
欧拉数的显式方程Explicit formula

插曲

斯特林数和欧拉数

嗯其实挺像的

欧拉数是把\([n]\)分成\(k\)个排列，每个排列都是上升的

第二类斯特林数\(S(n,r)\)是把\([n]\)分成\(r\)个集合

第一类斯特林数是把\([n]\)分成\(k\)个圆排列

它们之间联系的方程不要太多，没记错的话《具体数学》里有，这里不放了

(无符号)第二类斯特林数的显式方程

\[S(n, r)=\frac{1}{r !} \sum_{i=0}^{r}(-1)^{i}\left(\begin{array}{c} r \\ i \end{array}\right)(r-i)^{n} \]

欧拉数和生成函数

欧拉多项式的定义

对所有的非负整数\(n\)，多项式

\[A_{n}(x)=\sum_{k=1}^{n} A(n, k) x^{k} \]

is called the nth Eulerian polynomial.

欧拉多项式的显式方程

举例

\[A_{1}(x)=(1-x)^{2} \sum_{i>0} i x^{i}=(1-x)^{2} \cdot \frac{x}{(1-x)^{2}}=x \]

\[A_{2}(x)=(1-x)^{3} \sum_{i>0} i^{2} x^{i}=(1-x)^{3} \cdot\left(\frac{2 x^{2}}{(1-x)^{3}}+\frac{x}{(1-x)^{2}}\right)=x+x^{2} \]

研究欧拉数-a master GF

\[\begin{array}{c} \text {Let } r(x, u)=\sum_{n \geq 0} \sum_{k \geq 0} A(n, k) x^{k} \frac{u^{n}}{n !} . \text { Then we have} \\ r(x, u)=\frac{1-t}{1-t e^{u(1-t)}} \end{array} \]

。。。二重求和的时候把\(x\)和\(u\)当成形式变量

观察欧拉数金字塔研究性质

欧拉数金字塔长这样

给出一些实序列的property的定义

unimodal是说the sequence of positive real numbers \(a_{1}, a_{2}, \cdots, a_{n}\) is unimodal if there exists an index \(k\) such that \(1 \leq k \leq n,\) and \(a_{1} \leq a_{2} \cdots \leq a_{k} \geq a_{k+1} \geq a_{n}\)

log-concave是说the sequence of positive real numbers \(a_{1}, a_{2}, \cdots, a_{n}\) is \(\log\) concave if $ a_{k-1} a_{k+1} \leq a_{k}^{2}$ holds for all indices \(k\).

log-concave==>unimodal

一个正实数序列has real roots only (real zeros only) <==> \(\sum\limits_{i=1}^{n}a_ix^i\)只有实根

牛顿的定理：has real roots only=>log-concave

has real roots only=>序列要么有1个要么有2个最大值

欧拉多项式的所有根都是实的

\(A_{n}(x)=\sum\limits_{k=1}^{n} A(n, k) x^{k}\)的所有根都是实的

暂时写到这

资料来自网络

书用的是Combinatorics of permutations by Miklos Bona