【读书笔记】排列研究-逆序对

目录

• 生成函数
• 一开始的一些值
• 递归方程
• 递归方程-续
• 由生成函数找\(b(n,k)\)的显式表达式
  • Explicit formula
  • 书里所给证明的思路
• major index
• 联系行列式很是典型的那种定义
• 联系二分图的完美匹配
• 多重集构成的排列的逆序对

生成函数

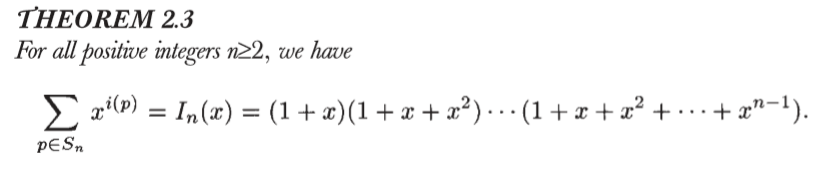
举例，比如\(n=3\)

排列有123，132，213，231，312，321

逆序对数分别是0，1，1，2，2，3

\[x^0+x^1+x^1+x^2+x^2+x^3=(1+x)(1+x+x^2) \]

课本给出的一个简单的证明是使用数学归纳法：

当\(n=2\)时，当然\(1+x\)

如果对\(n-1\)成立的话，那么考虑n-1排列的\(n\)个位置插入元素\(n\)，分别会使逆序对数+0，+1，+2，+3，...，+(n-1)。这就解释了GF又乘上\(1+x+...+x^{n-1}\)

记\(b(n,k)\)是\(I_n(x)\)的\(x^k\)前的系数，也是长度为\(n\)且逆序对数为\(k\)的排列的个数

一开始的一些值

http://oeis.org/A008302

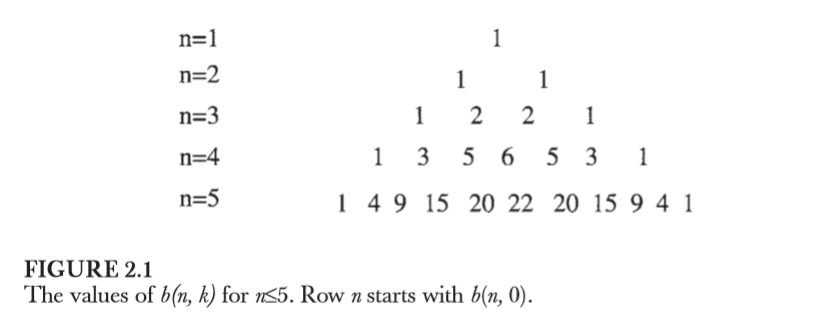
递归方程

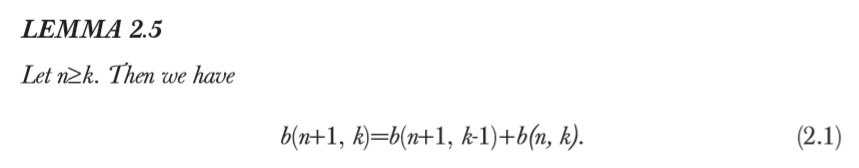
此递归方程的适用条件是\(n\geq k\)

证明是说考察n+1-排列的最后一个元素：

如果是\(n+1\),那么\(n+1\)在的数对不贡献，

所以【n+1-排列且k个逆序对，with最后一个元素是\(n+1\)】的数目和【n-排列且k个逆序对】构成bijection(变换只是末尾删/增\(n+1\))，数目相等。

 
如果不是\(n+1\)，\(n+1\)在前n个数里。把\(n+1\)和紧跟其后的元素交换，逆序对数目会减少1，这样得到的新的n+1-排列与原来的n+1-排列构成bijection，数目自然一致。

操作后的序列是【n+1-排列且k-1个逆序对，with第一个元素不是\(n+1\)】，按理来说我们应该算这种序列有多少个。但是如果强加上\(n\geq k\),这样【n+1-排列且k-1个逆序对】的第一个元素肯定不能是\(n+1\)了，改为数数【n+1-排列且k-1个逆序对】

于是，【n+1-排列且k个逆序对，with最后一个元素不是\(n+1\)】的数目和【n+1-排列且k-1个逆序对】数目相等。

递归方程-续

28. Let \(n<k \leq\left(\begin{array}{l}n \\ 2\end{array}\right)\). Prove that

\[b(n+1, k)=b(n+1, k-1)+b b(n, k)-b(n, k-n-1) \]

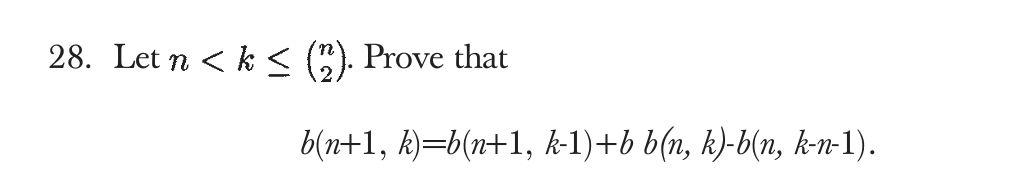
吐槽一下这个抽风印刷，另一个地方tu ple 还分开写。。。。

由生成函数找\(b(n,k)\)的显式表达式

Explicit formula

直接出击，由生成函数的形式联想到有限制的把\(k\)分解成\(n-1\)部分的compositon

\[\begin{array}{ll} b(n, 0)=1=\left(\begin{array}{c} n \\ 0 \end{array}\right) \\ b(n, 1)=n-1=\left(\begin{array}{c} n \\ 1 \end{array}\right)-\left(\begin{array}{c} n \\ 0 \end{array}\right) & n \geq 1 \\ b(n, 2)=\left(\begin{array}{c} n \\ 2 \end{array}\right)-\left(\begin{array}{c} n \\ 0 \end{array}\right), & n \geq 2 \\ b(n, 3)=\left(\begin{array}{c} n+1 \\ 3 \end{array}\right)-\left(\begin{array}{c} n \\ 1 \end{array}\right) & n \geq 3 \\ b(n, 4)=\left(\begin{array}{c} n+2 \\ 4 \end{array}\right)-\left(\begin{array}{c} n+1 \\ 2 \end{array}\right) & n \geq 4 \\ b(n, 5)=\left(\begin{array}{c} n+3 \\ 5 \end{array}\right)-\left(\begin{array}{c} n+2 \\ 3 \end{array}\right)+1 & n\geq 5 \end{array} \]

然后就猜啊这个\(b(n,k)\)的形式是不是就是简单的组合数正负交错和的形式啊？

答案是否定的，形式比我们想的还要复杂一点

五边形数是啥意思啊，是\(\frac{1}{2}\left(3 j^{2} \pm j\right)\)的形式

书里所给证明的思路

书里给出的证明是说先证明这个 Euler's formula

\[\begin{aligned} f(x)=(1-x)\left(1-x^{2}\right)\left(1-x^{3}\right) \cdots &=1-x-x^{2}+x^{5}+x^{7}-x^{12}-\cdots \\ &=\sum_{j>-\infty}^{\infty}(-1)^{j} x^{\left(3 j^{2}+j\right) / 2} \end{aligned} \]

然后因为研究的GF可以写成这样的形式

\[I_{n}(x)=\prod_{i=1}^{n}\left(1+x+\cdots x^{i-1}\right)=\prod_{i=1}^{n} \frac{1-x^{i}}{1-x} \]

所以

\[f(x) \cdot(1-x)^{-n}=f(x) \cdot \sum_{h \geq 0}\left(\begin{array}{c} n+h-1 \\ h \end{array}\right) x^{h}=I_n(x) \]

\[\sum_{j>-\infty}^{\infty}(-1)^{j} x^{\left(3 j^{2}+j\right) / 2}\cdot \sum_{h \geq 0}\left(\begin{array}{c} n+h-1 \\ h \end{array}\right) x^{h}=I_n(x) \]

比对可知\(b(n,k)\)（即\(I_n(x)\)中\(x^k\)项系数）有这样的形式

\[b(n, k)=\sum_{j}(-1)^{j}\left(\begin{array}{c} n+k-d_{j}-1 \\ k-d_{j} \end{array}\right) \]

major index

说一个排列的逆序对数还可能由其他的看起来的很不相关的统计推导出来

定义一个排列的major index是所有的降位的下标和

举例一个排列是352461，那么它的降位置集是[2,5]，因此，此排列的major index是7

值得注意的是，只是说分布是一样的，一个permutation的逆序对数和major index不一定相等

我都呆了我都，这为啥也能相等啊。。。。。1916年说它们数目一样，到1968年才找到bijection.证明太长了这里不放了
找到构造的那篇论文地址
我感觉太晦涩了，我看的是这篇文章的算法。

我写了一份演示该算法的Mathematica代码，点击查看代码

(* 我写了一份演示该算法的Mathematica代码 *)
TransformPhi[s_List] := Module[{n, w, splitAndMove}, n = Length[s];
  w[1] = {s[[1]]};
  splitAndMove[list_, value_, compFunc_] := 
   Module[{positions, segments}, 
    positions = Flatten[Position[list, _?compFunc]];
    If[Length[positions] == 0, Return[{list}]];
    positions = {0}~Join~positions;
    segments = 
     Table[list[[(positions[[i - 1]] + 1) ;; positions[[i]]]], {i, 2, 
       Length[positions]}];
    Join @@ (RotateRight[#, 1] & /@ segments)];
  Do[If[Last[w[k - 1]] > s[[k]], 
     w[k] = Join[
       splitAndMove[w[k - 1], s[[k]], # > s[[k]] &], {s[[k]]}], 
     w[k] = Join[
       splitAndMove[w[k - 1], s[[k]], # < s[[k]] &], {s[[k]]}]];
   , {k, 2, n}];
  w[n]]

(*Test*)
TransformPhi[{7, 4, 9, 2, 6, 1, 5, 8, 3}]


TransformPhiInverse[inputv_List] := 
 Module[{n, s, v, splitAndMove}, n = Length[inputv];
  s[n] = Last[inputv];
  v[n - 1] = Most[inputv];
  splitAndMove[list_, value_, compFunc_] := 
   Module[{positions, segments, breakPts}, 
    positions = Flatten[Position[list, _?compFunc]] - 1;
    If[Length[positions] == 0, Return[{list}]];
    breakPts = Append[1 + positions, Length[list] + 1];
    segments = 
     Table[list[[breakPts[[i]] ;; breakPts[[i + 1]] - 1]], {i, 
       Length[breakPts] - 1}];
    Join @@ (RotateLeft[#, 1] & /@ segments)
    ];
  Do[
   If[v[k][[1]] > s[k + 1], 
    v[k - 1] = splitAndMove[v[k], s[k + 1], # > s[k + 1] &],
    v[k - 1] = splitAndMove[v[k], s[k + 1], # < s[k + 1] &]];
   s[k] = Last[v[k - 1]];
   If[k >= 2, v[k - 1] = Drop[v[k - 1], -1]];
   , {k, n - 1, 1, -1}
   ];
  
  Array[s, n]
  ]

(*Test*)
TransformPhiInverse[{6, 4, 9, 7, 2, 5, 8, 1, 3}]



n = 5;
MajorIndex[perm_List] := 
  Sum[If[perm[[i]] > perm[[i + 1]], i, 0], {i, Length[perm] - 1}];
InversionNumber[perm_List] := 
  Length[Select[Subsets[Range[Length[perm]], {2}], 
    perm[[#[[1]]]] > perm[[#[[2]]]] &]];
permutations = Permutations[Range[n]];



MajorIndex /@ permutations // Tally // Sort
InversionNumber /@ permutations // Tally // Sort


(InversionNumber@*TransformPhi) /@ permutations // Tally // Sort
(MajorIndex@*TransformPhi) /@ permutations // Tally // Sort
((InversionNumber@*TransformPhi@# - MajorIndex@#) &) /@ permutations


(InversionNumber@*TransformPhiInverse) /@ permutations // Tally // Sort
(MajorIndex@*TransformPhiInverse) /@ permutations // Tally // Sort
((MajorIndex@*TransformPhiInverse@# - InversionNumber@#) &) /@ permutations

联系行列式很是典型的那种定义

\[\operatorname{det} A_{i j}=\sum_{q}(-1)^{i(q)}{a_{1 q_{1}}} a_{2 q_{2}} a_{3 q_{3}} \cdots a_{n q_{n}} \]

联系二分图的完美匹配

先空着

多重集构成的排列的逆序对

资料来自网络

书用的是Combinatorics of permutations by Miklos Bona