2022 1-18

 

题目：

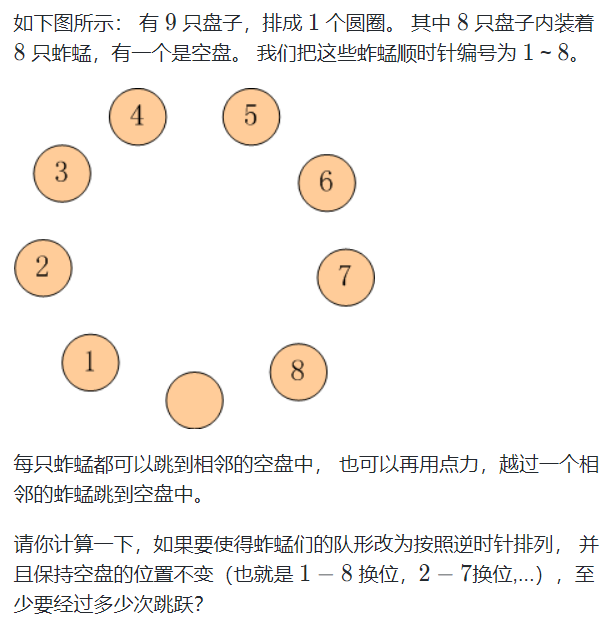
题解：

BFS
策略︰我们将当前的局面用字符串保存，例如初始的局面是“012345678”，用广搜的办法来搜索最小的步数。

去重∶广搜深搜都有剪枝的问题，目的就是去除不可能的分支，提高效率，

这里我用了STL的set容器来判重，在搜到一种局面后，在set里对这个局面进行查找，如果存在的话，就说明已经搜索过这个局面了，如果没有，则加入set.

代码：

 

#include <iostream>
#include <bits/stdc++.h>

using namespace std;
int a[10];
int d[5]={ -1,1,2,-2 };
struct node{
    int x;
    int pos;
    int sp;
};
queue<node> p;

int getsum(){
    int sum=0;
    for(int i=0;i<=8;i++)
        sum=sum*10+a[i];
    return sum;
}

void delive(int x){
    for(int i=8;i>=0;i--)
        a[i]=x%10,x/=10;
}
 set<int>mp;
int bfs(){
    int sum=getsum();
    node v;
    v.pos=0;v.sp=0;v.x=sum;
    p.push(v);
    while(!p.empty()){
        node now=p.front();
        p.pop();
        if(now.x==87654321) return now.sp;
        if(mp.find(now.x)!=mp.end()) continue;
        mp.insert(now.x);
        delive(now.x);
        for(int i=0;i<4;i++){
        int cur=(now.pos+d[i]+9)%9;
        swap(a[cur],a[now.pos]);
        int temp=getsum();
        node vv;
        vv.pos=cur; vv.sp=now.sp+1; vv.x=temp;
        p.push(vv);
        swap(a[cur],a[now.pos]);
        }
    }
}


int main()
{
    for(int i=0;i<=8;i++)
        a[i]=i;
   cout<<bfs()<<endl;
    return 0;
}

 

 

魔方状态：

归于魔方理论领域了。例如二阶有3674160种不同的改动，核算的时分先断定方位，再断定色相，最终扫除不能恢复的状况。

具体算法：

有一个角需要用来定位，7个角块全摆放，是7！个，

然后每个角块有三种色相（即正确，正确块顺时针转一次，正确块逆时针转一次，就这三种），所以数量是3^7（这是三的7次方），方才这两个相乘作为分子。

然后，独自一个角块色是不能变化的（即要固定 总共三种色相），所以要除以3；

3阶魔方所有改动数为7！×3^6=3674160种。  

三阶魔方总改动数的道理是这样：

六个中心块定好朝向后，咱们就不能够翻转魔方了，而他们也正好构成了一个坐标系，在这个坐标系里：

8个角块全摆放8!，而每个角块又有3种朝向，所以是8!*3^8，

12个棱色块全摆放每个有2种朝向是12!*2^12，这样相乘就是分子;

而分母上3*2*2的含义是:

坚持其他色块不动，不能够独自改动一个角块朝向，改动一个棱色块朝向，和独自交换一对棱色块或一对角块的方位。

K倍区间

思路：

核心思想: 两个前缀和模k的值相同的区间，可以产生一个k倍区间。

 

代码：

#include <iostream>
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll a[100005],sum[100005]={0};
map<ll,ll> mp;

ll slove(ll x){
    return x*(x-1)/2;
}

int main()
{
    ll cnt=0;
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        sum[i]=sum[i-1]+a[i];
    }
    for(int i=1;i<=n;i++){
     int kk=sum[i]%k;
     if(kk==0) cnt++;
      mp[kk]++;
    }
    for(auto x:mp)
       cnt+=slove(x.second);
    cout<<cnt<<endl;
    return 0;
}

https://codeforces.com/contest/1627/problem/D

思路：

两个数字的 gcd不能超过它们的最大值。 设数组的最大元素为 A。 

因此，对于从 1 到 A 的每个数字，我们尝试在执行一些操作后检查该元素是否可以包含在数组中。

如何检查特定数字x？要使 x 在最终数组中

1.它已经存在于初始数组中。

2.初始数组中存在的所有 x 倍数的 gcd 等于 x

代码：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int MAXV = 1e6;
 
int gcd(int x,int y){
	return (y==0)?x:gcd(y,x%y);
}
void solve()
{
    int n,x; 
    cin>>n;
    int ans[MAXV+5]={0}, tot=0;
    for(int i=1;i<=n;i++) 
        cin>>x, ans[x]=1;
 
    for(int i=1;i<=MAXV;i++) {
        if(ans[i]==1) continue;// 如果有就跳过
        ll t=0;
        for(int j=i;j<=MAXV;j+=i)
          if(ans[j]) 
              t=gcd(t,j);//0与任意数的最大公约数是该任意数本身
        if(t==i) tot++;
    }
    cout<<tot<<endl;
}
 
int main(){
   int t;
cin>>t;
while(t--)
    solve();
    return 0;
}