lca 科技

完全二叉树求 lca

https://blog.csdn.net/kksleric/article/details/7836649

先考虑完全二叉树的 lca 求法。中序遍历分配编号。

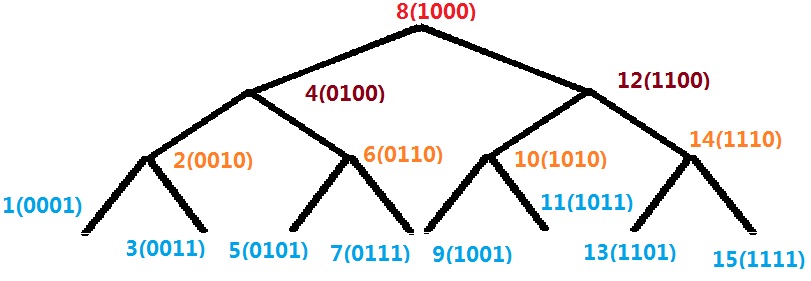
设第 \(k\) 位是 \(u\oplus v\) 最左边的 \(1\)，则 \(lca(u,v)\) 是 \(u,v\) 的 \(k\) 位以左、第 \(k\) 位是 \(1\)，\(k\) 位以右是 \(0\)。

将树上 lca 转到完全二叉树上。

先序遍历，设 \(h_u\) 表示 \(dfn_u\) 的末尾连续 \(0\) 数，\(l_u\) 表示 \(u\) 子树内最大 \(h_u\) 的值，\(mx_u\) 表示 \(l_u\) 对应的 \(dfn_u\) 。相等的 \(mx_u\) 形成若干条链。有若 \(tp\) 是 \(u\) 的祖先，\(mx_{tp}\) 是 \(mx_u\) 完全二叉树中的祖先。

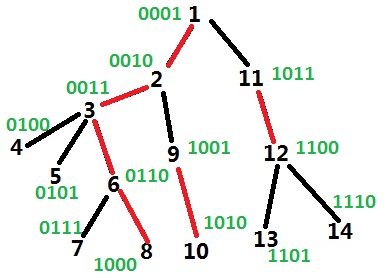
设 \(tp=lca(u,v)\)。则 \(mx_{tp}\) 是 \(mx_u,mx_v\) 的公共祖先。树上根到节点路径上 \(l_u\) 单调不降，但在树上的 \(mx_u\) 值不连续。设 \(a_u\) 表示从根到 \(u\) 哪些 \(l_u\) 值存在。可以求出 \(mx_u\) 和 \(mx_v\) 在完全二叉树上的 lca 的末尾零数 \(d\)，在 \(a_u\) 和 \(a_v\) 中都出现的最小的 \(s\ge d\) 就是 \(mx_{tp}\) 的末尾零数。

每种 \(mx_u\) 值都会形成一条链。找到 \(u,v\) 到链 \(mx_{tp}\) 上的最近祖先深度较小的一个即为 lca。可以找到 \(a_u,a_v\) 中小于 \(s\) 的最大的 \(du,dv\)，这条链的链顶的父亲在链 \(mx_{tp}\) 上。

预处理 \(O(n)\)，查询 \(O(1)\)，空间 \(O(n)\)。理论上完全偏序所有 lca 算法。

int idx,dfn[maxn],rnk[maxn],l[maxn],fa[maxn],dep[maxn];
void dfs(int u){
	dep[u]=dep[fa[u]]+1;
	rnk[dfn[u]=++idx]=u;l[u]=__builtin_ctz(idx);
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;if(v==fa[u])continue;
		fa[v]=u;dfs(v);
		l[u]=max(l[u],l[v]);
	}
}
int tp[maxn];unsigned int a[maxn];
void dfs1(int u,int lst){
	a[u]=a[fa[u]]|(1<<l[u]);tp[u]=lst;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;if(v==fa[u])continue;
		if(l[u]==l[v])dfs1(v,lst);
		else dfs1(v,v);
	}
}
int lca(int u,int v){
	if(u==v)return u;
	int d=31^__builtin_clz(dfn[u]^dfn[v]);
	int s=__builtin_ctz(((a[u]&a[v])>>d)<<d);
	int du=31^__builtin_clz(a[u]<<(32-s)>>(32-s)),uu=(l[u]!=s?fa[tp[rnk[((dfn[u]>>du)|1)<<du]]]:u);
	int dv=31^__builtin_clz(a[v]<<(32-s)>>(32-s)),vv=(l[v]!=s?fa[tp[rnk[((dfn[v]>>dv)|1)<<dv]]]:v);
	if(dep[uu]<dep[vv])return uu;
	return vv;
}

dfn 序 ST 表

\(u\) 的 dfn 序到 \(v\) 的 dfn 序之间必然不存在存在 \(lca(u,v)\) 和 \(lca(u,v)\) 的祖先，必然存在 \(lca(u,v)\) 的儿子。\(u\) 的 dfn 序到 \(v\) 的 dfn 序之间深度最小的点的父亲为 \(lca(u,v)\)。

预处理 \(O(n\log n)\)，查询 \(O(1)\)，空间 \(O(n\log n)\)。

int dfn[maxn],idx;
int st[20][maxn];
void dfs(int u,int fa){
	st[0][dfn[u]=++idx]=fa;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v!=fa)dfs(v,u);
	}
}
int lca(int u,int v){
	if(u==v)return u;
	u=dfn[u],v=dfn[v];
	if(u>v)swap(u,v);u++;
	int k=log2(v-u+1);
	if(dfn[st[k][u]]<dfn[st[k][v-(1<<k)+1]])return st[k][u];
	return st[k][v-(1<<k)+1];
}
void init(){
	for(int j=1;j<20;j++){
		for(int i=1;i+(1<<j)-1<=n;i++){
			if(dfn[st[j-1][i]]<dfn[st[j-1][i+(1<<j-1)]])st[j][i]=st[j-1][i];
			else st[j][i]=st[j-1][i+(1<<j-1)];
		}
	}
}

倍增

预处理 \(O(n\log n)\)，查询 \(O(\log n)\)，空间 \(O(n\log n)\)，常数大。

int dep[maxn],f[maxn][21];
void dfs(int u,int fa){
	dep[u]=dep[fa]+1;f[u][0]=fa;
	for(int i=1;i<=20;i++)f[u][i]=f[f[u][i-1]][i-1];
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;if(v==fa)continue;
		dfs(v,u);
	}
}
int lca(int x,int y){
	if(dep[x]>dep[y])swap(x,y);
	for(int i=20;i>=0;i--)if(dep[f[y][i]]>=dep[x])y=f[y][i];
	if(x==y)return x;
	for(int i=20;i>=0;i--)if(f[y][i]!=f[x][i])x=f[x][i],y=f[y][i];
	return f[x][0];
}

树剖

预处理 \(O(n)\)，查询 \(O(\log n)\)，极难卡满，空间 \(O(n)\)。

int dep[maxn],fa[maxn],siz[maxn],son[maxn];
void dfs(int u){
	dep[u]=dep[fa[u]]+1;siz[u]=1;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v!=fa[u]){
			fa[v]=u;
			dfs(v);
			siz[u]+=siz[v];
			if(siz[v]>siz[son[u]])son[u]=v;
		}
	}
}
int dfn[maxn],idx,rnk[maxn],tp[maxn];
void dfs2(int u,int lst){
	rnk[dfn[u]=++idx;]=u;tp[u]=lst;
	if(!son[u])return ;
	dfs2(son[u],lst);
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v!=fa[u]&&v!=son[u])dfs2(v,v);
	}
}
int lca(int u,int v){
	while(tp[u]!=tp[v]){
		if(dep[tp[u]]<dep[tp[v]])swap(u,v);
		u=fa[tp[u]];
	}
	if(dep[u]>dep[v])swap(u,v);
	return u;
}