完整教程：【卷积神经网络详解与实例】4——感受野

4、感受野

4.1 感受野的概念

在卷积神经网络中，感受野（Receptive Field）是一个极其要紧的概念，它描述了卷积神经网络中某一层输出结果的一个元素对应输入层上的区域大小，也就是特征图（Feature Map）上的一个点所对应的输入图像上的区域。

通过神经元之所以无法对原始图像的所有信息进行感知，是因为在这些网络结构中普遍采用卷积层和池化层，在层与层之间均为局部相连。神经元感受野的值越大表示其能接触到的原始图像范围就越大，也意味着他可能蕴含更为全局、语义层次更高的特征；而值越小则表示其所具备的特征越趋向于局部和细节。因此感受野的值能够大致用来判断每一层的抽象层次。

4.2 感受野大小的计算

4.2.1 公式推导

我们先看下面这个例子：

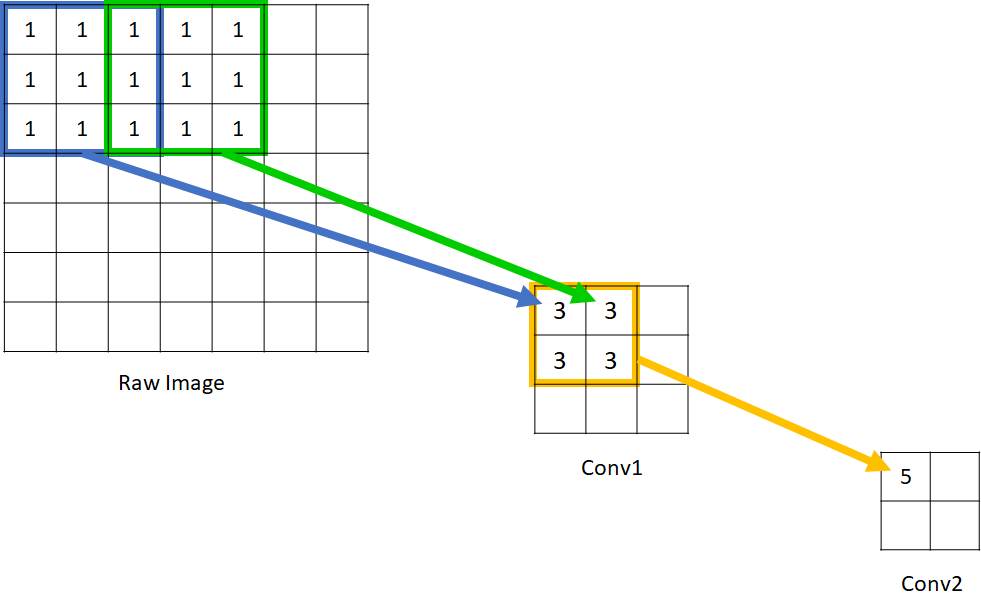
可以看到在Conv1中的每一个单元所能看到的原始图像范围是 3*3，而由于 Conv2 的每个单元都是由 2*2 范围的 Conv1 构成，因此回溯到原始图像，能够看到的原始图像范围是 5*5 。因此我们说 Conv1 的感受野是 3，Conv2 的感受野是 5. 输入图像的每个单元的感受野被定义为 1，这应该很好理解，因为每个像素只能看到自己。

多大，但对于层数过多、过于复杂的网络结构来说，用这种办法可能就不够聪明了。因此我们希望能够归纳出这其中的规律，并用公式来描述，这样就可以对任意复杂的网络结构计算其每一层的感受野了。就是通过上图这种图示的方式我们可以“目测”出每一层的感受野

由于图像是二维的，具有空间信息，因此感受野的实质其实也是一个二维区域。但业界通常将感受野定义为一个正方形区域，因此也就采用边长来描述其大小了。在接下来的讨论中，本文也只考虑宽度一个方向。我们先按照下图所示对输入图像的像素进行编号。

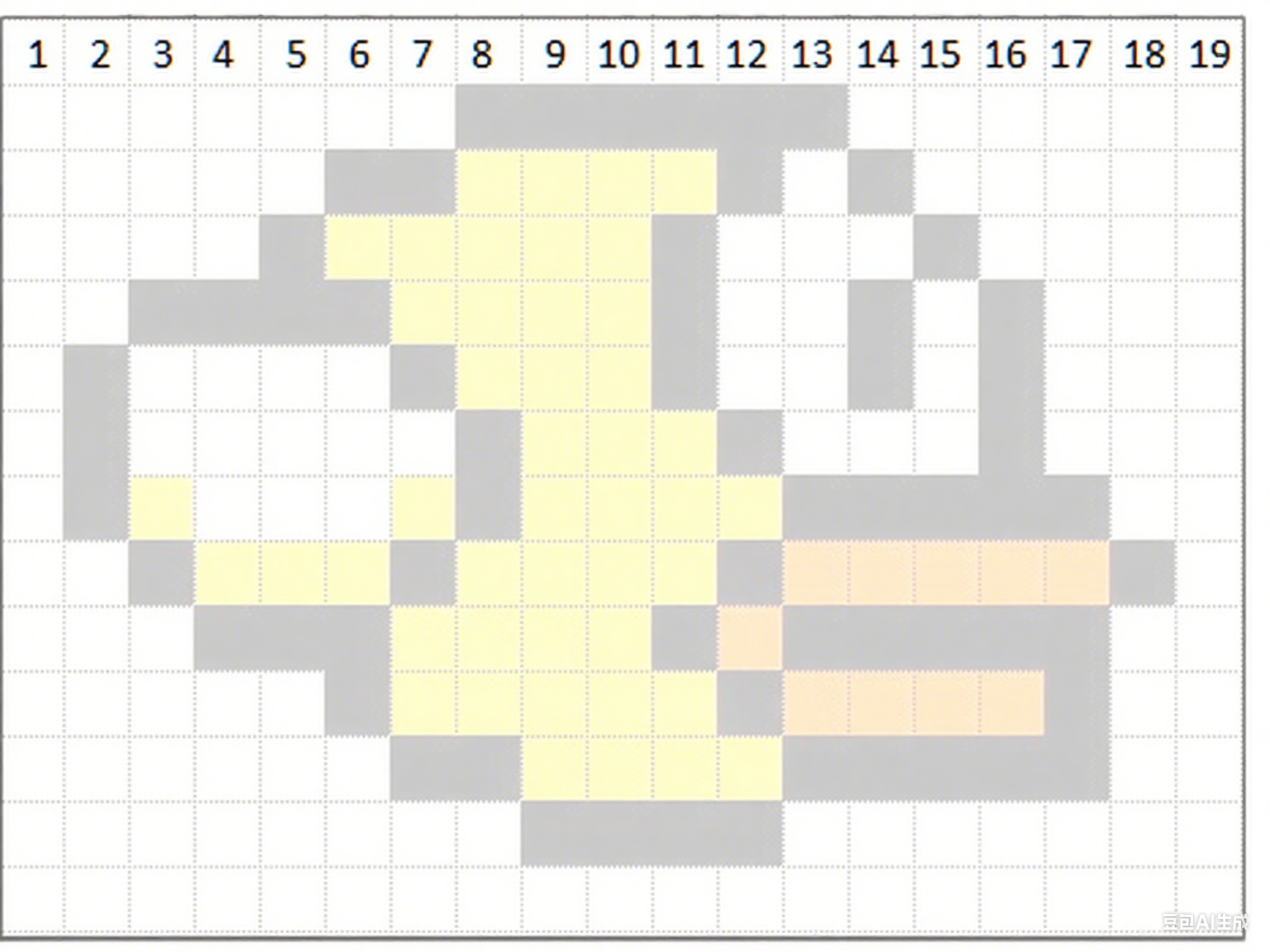
接下来大家使用一种并不常见的方式来展示CNN的层与层之间的关系（如下图，请将脑袋向左倒45°观看），并且配上对原图像的编号。

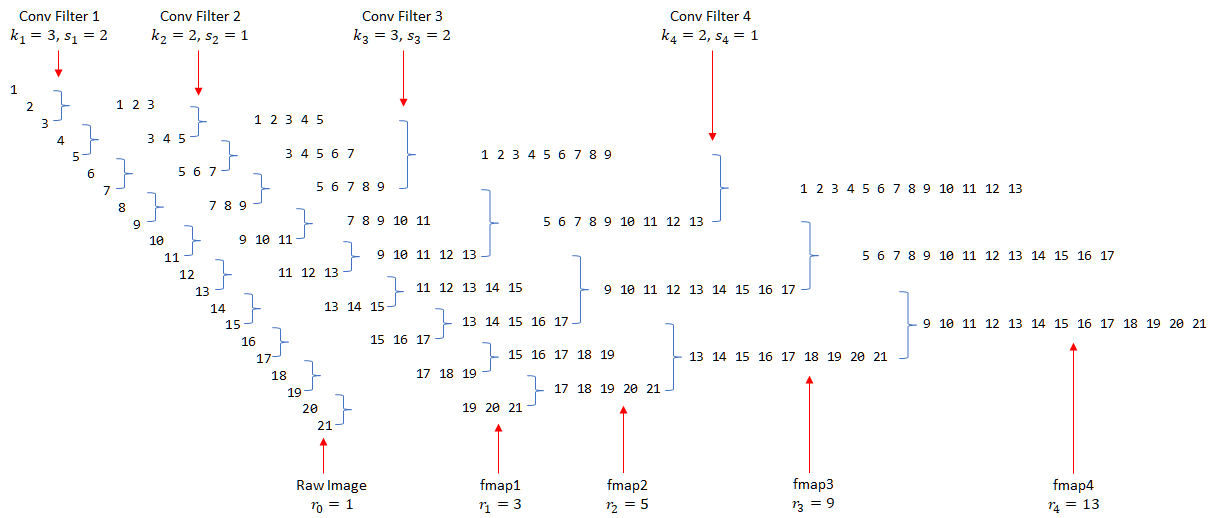
图中黑色的数字所构成的层为原图像或者是卷积层，数字表示某单元能够看到的原始图像像素。我们用来表示第 n 个卷积层中每个单元的感受野（即数字序列的长度）；蓝色的部分表示卷积操控，用和分别表示第 i 个卷积层的 kernel_size 和 stride 。

对 Raw Image 进行 kernel_size=3, stride 2 的卷积运行所得到的 fmap1（fmap为feature map的简称，为每一个conv层所产生的输出）的结果是显而易见的。序列 [1 2 3] 表示 fmap1 的第一个单元能看见原图像中的 1, 2, 3 这三个像素，而第二个单元则能看见 3, 4, 5。这两个单元随后又被 kernel_size=2, stride=1 的 Filter 2 进行卷积，因而得到的 fmap2 的第一个单元能够看见原图像中的 1,2,3,4,5 共5个像素（即取 [1 2 3] 和 [3 4 5] 的并集）。

接下来我们尝试一下如何用公式来表述上述过程。许可看到，[1 2 3] 和 [3 4 5] 之间由于 Filter1 的 stride=2 而错开（偏移）了两位，而3是重叠的。对于卷积两个感受野为3的上层单元，下一层最大能获得的感受野为 $3 \times 2 = 6$ 2。因此我们就得到就是，但因为有重叠，因此要减去(kernel_size - 1)个重叠部分，而重叠部分的计算方式则为感受野减去前面所说的偏移量，这里 $r_2 = r_1 \times k_2 - (r_1 - s_1) \times (k_2 - 1) = 3 \times 2 - (3 - 2) \times (2 - 1) = 5$ 。继续往下一层看，我们会发现[1 2 3 4 5]和[3 4 5 6 7]的偏移量仍为2，并不简单地等于上一层的，这是因为之前的stride对后续层的影响是永久性的，而且是累积相乘的关系（例如，在fmap3中，偏移量已经累积到4了），也就是说应该这样求

$r_3 = r_2 \times k_3 - (r_2 - s_1 \times s_2) \times (k_3 - 1) = 5 \times 3 - (5 - 2) \times (3 - 1) = 9$

以此类推，

$r_4 = r_3 \times k_4 - (r_3 - s_1 \times s_2 \times s_3) \times (k_4 - 1) = 9 \times 2 - (9 - 4) \times (2 - 1) = 13$

于是我们就可以得到关于计算感受野的抽象公式了：

$r_n = r_{n-1} \times k_n - (r_{n-1} - \prod_{i=1}^{n-1} s_i) \times (k_n - 1) \\ = r_{n-1} + (k_n - 1) \prod_{i=1}^{n-1} s_i$

3.2.2 具体应用举例

使用公式 $r_n = r_{n-1} + (k_n - 1) \prod_{i=1}^{n-1} s_i$ 计算AlexNet每层的感受野。

AlexNet 的相关数据如下：

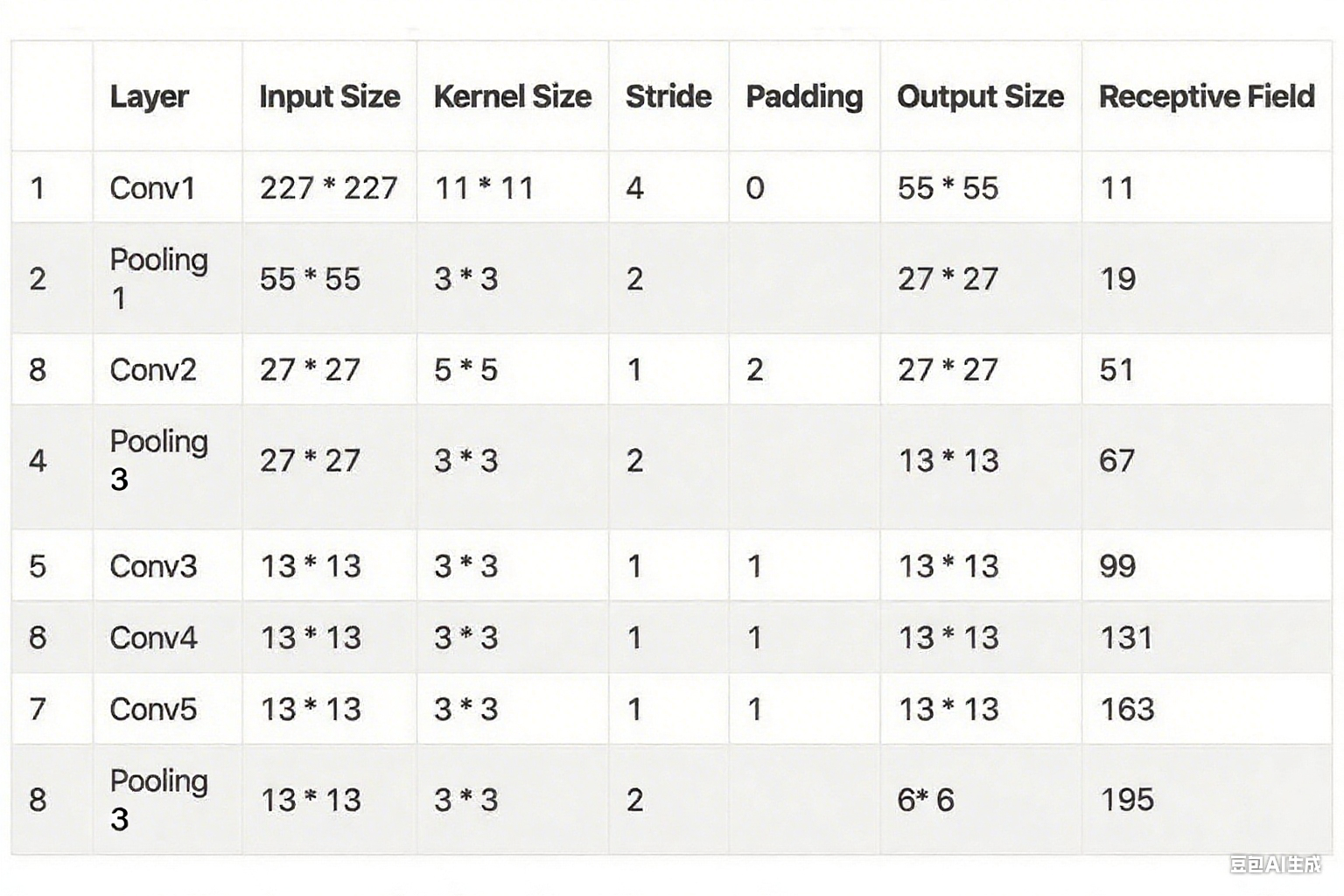
原始图像，感受野为：
$Conv1 = 1 + (11-1) \times 1 = 11$
$Pooling1 = 11 + (3-1) \times (1\times4) = 19$
$Conv2 = 19 + (5-1) \times (1\times4\times2) = 51$
$Pooling2 = 51 + (3-1)\times(1\times4\times2\times1) = 67$
$Conv3 = 67 + (3-1)\times(1\times4\times2\times1\times2) = 99$
$Conv4 = 99 + (3-1)\times(1\times4\times2\times1\times2\times1) = 131$
$Conv5 = 131 + (3-1)\times(1\times4\times2\times1\times2\times1\times1)= 163$
$Pooling3 = 163 + (3-1)\times(1\times4\times2\times1\times2\times1\times1\times1) = 195$

3.2.3 感受野大小的变与不变

任何“让单层像素能看到更多/更少输入区域”的操控就能改感受野；只做“通道混合”或“像素重排”而不看更大/更小区域的，就不能。

✅ 能改变感受野的层（看到更大/更小区域）

操作	方向	记忆口诀
普通卷积(k>1)	变大	“核>1 就多扫一圈”
空洞卷积(dilation)	变大	“空一格看一次，视野成倍”
池化/下采样(stride>1)	变大	“一步跨多格，后面层等价看更大”
转置卷积(deconv)	变大	“上采样，把 1 像素扩散成 block”
大 stride 卷积	变大	“ stride=2 等价把后面感受野×2”
1×1 卷积	不变	只看单点，不扩大也不缩小

❌ 不能改变感受野的层（只动通道，不动空间视野）

操作	原因一句话
1×1 卷积	只混通道，单像素仍只看原像素
BatchNorm / LayerNorm	归一化系数，空间位置无关
ReLU、Sigmoid、GELU	逐点激活，无邻居信息
Dropout / DropBlock	随机失活，不改变实际视野
通道拼接/相加(concat/add)	把各支路结果汇总，各支路感受野已固定就是只
通道打乱(shuffle)	像素没动，只是重排通道顺序

padding本身不改感受野大小，只改特征图尺寸；它让“边缘像素也能被正常扫描”，所以常配合大 kernel/dilation 使用。
多分支结构(Inception、ResNet) 的最终感受野 =各分支最大者；相加/拼接不会把小的变大。

posted @ 2025-09-11 18:24 yfceshi 阅读(88) 评论(0) 收藏举报

刷新页面返回顶部