网络流详解+题目
介绍
首先先了解网络和流

再了解一下网络流的相关定义:
- 源点:有n个点,有m条有向边,有一个点很特殊,只出不进,叫做源点。
- 汇点:另一个点也很特殊,只进不出,叫做汇点。
- 容量和流量:每条有向边上有两个量,容量和流量,从i到j的容量通常用c[i,j]表示,流量则通常是f[i,j].
- 残量:就是当前容量减去流量
网络流的常见问题
网络流问题中常见的有以下三种:最大流,最小割,费用流。
最大流
1、我们有一张图,要求从源点流向汇点的最大流量(可以有很多条路到达汇点),就是我们的最大流问题。
最小费用最大流
2、最小费用最大流问题是这样的:每条边都有一个费用,代表单位流量流过这条边的开销。我们要在求出最大流的同时,要求花费的费用最小。
最小割
3、割其实就是删边的意思,当然最小割就是割掉 \(X\) 条边来让 \(S\) 跟 \(T\) 两个集合(可以理解为 源点\(S\) 和 汇点\(T\) 不连通)不互通。我们要求 \(X\) 条边加起来的流量总和最小。这就是最小割问题。
1. 求最大流
首先,明确最大流是干什么的
给定指定的一个有向图,其中有两个特殊的点源S(Sources)和汇T(Sinks),每条边有指定的容量(Capacity),求满足条件的从S到T的最大流(MaxFlow).
通俗一点,
就好比你家是汇 自来水厂是源
然后自来水厂和你家之间修了很多条水管子接在一起 水管子规格不一 有的容量大 有的容量小
然后问自来水厂开闸放水 你家收到水的最大流量是多少
如果自来水厂停水了 你家那的流量就是0 当然不是最大的流量
但是你给自来水厂交了100w美金 自来水厂拼命水管里通水 但是你家的流量也就那么多不变了 这时就达到了最大流
理解起来还好吧,也就是上文说的那样
1.1Edmond-Karp算法
1.1.1 算法解析
首先引入增广路的概念:
- 增广路
在原图\(G\)中若一条从源点到汇点的路径上所有边的 ** 剩余容量都大于\(0\) **,这条路被称为增广路
通俗一点
在原图 \(G\) 中若一条从源点到汇点的路径上所有边的 剩余容量都大于 \(0\),这条路被称为增广路(Augmenting Path)。
通过定义,我们显然可以看出求最大流其实就是不断寻找增广路的过程。
可以用BFS也可以用DFS,只是BFS快一点
详细一点:就是用 BFS 找增广路,然后对其进行增广。你可能会问,怎么找?怎么增广?
1、找?我们就从源点一直 BFS 走来走去,碰到汇点就停,然后增广(每一条路都要增广)。我们在 BFS 的时候就注意一下流量合不合法就可以了。
2、增广?其实就是按照我们找的增广路在重新走一遍。走的时候把这条路的能够成的最大流量减一减,然后给答案加上最小流量就可以了。
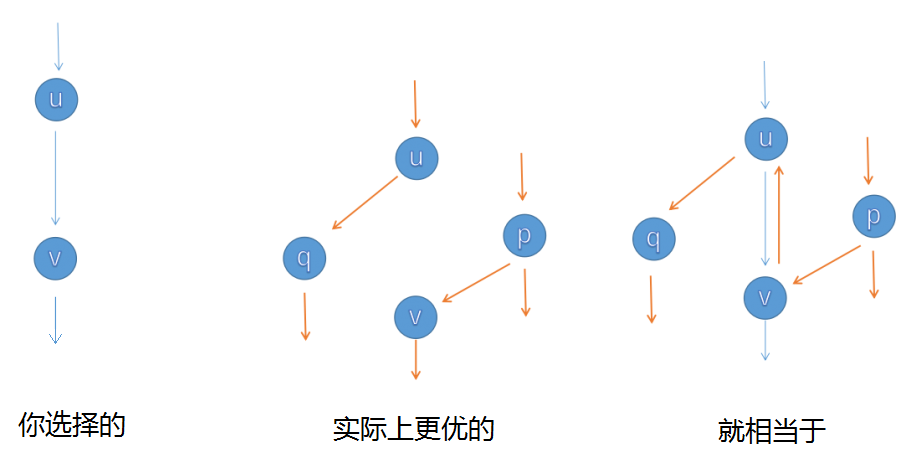
再讲一下 反向边。增广的时候要注意建造反向边,原因是这条路不一定是最优的,这样子程序可以进行反悔(就相当于蓝色和橙色的线抵消了。)。假如我们对这条路进行增广了,那么其中的每一条边的正向边就减去流量,反向边的流量就加上它的流量。
1.1.2 复杂度
EK 算法的时间复杂度为 \(O(nm^2)\) (其中 \(n\) 为点数, \(m\) 为边数)。效率还有很大提升空间。
1.1.3 模板
#include <bits/stdc++.h>
using namespace std;
int cnt=1;
int n,m,s,t;
int u,v,w;
bool vis[205];
int head[205];
struct o{
int pre,edge;
}p[10005];
struct node{
int next,to,w;
}e[10005];
void add(int x,int y,int w){
e[++cnt].w=w;
e[cnt].to=y;
e[cnt].next=head[x];
head[x]=cnt;
}
bool dfs(){
queue<int>q;
memset(vis,0,sizeof(vis));
q.push(s);
vis[s]=1;
while (!q.empty()){
int top=q.front();
q.pop();
for (int i=head[top];i;i=e[i].next){
if (!vis[e[i].to]&&e[i].w){//若没去过且容量大于0
vis[e[i].to]=1;//标记去过
p[e[i].to].edge=i;//记录路径,edge为边
p[e[i].to].pre=top;//记录路径,pre为上一个点
if (e[i].to==t){
return 1;
}q.push(e[i].to);
}
}
}return 0;//若全部搜完还没有出现增广路,返回0
}
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
for (int i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v,u,0);
}
long long ans=0;
while (dfs()){
int minn=999999999;
for (int i=t;i!=s;i=p[i].pre) //找最小容量
minn=min(minn,e[p[i].edge].w);
for (int i=t;i!=s;i=p[i].pre){//更改
e[p[i].edge].w-=minn;
e[p[i].edge^1].w+=minn;
}
ans+=minn;
}
printf("%lld",ans);
return 0;
}
1.2 Dinic算法
1.2.1 算法思路
Dinic算法的思想也是分阶段地在层次网络中增广。每次增广前,我们先用 BFS 来将图分层。设源点的层数为 ,那么一个点的层数便是它离源点的最近距离。
通过分层,我们可以干两件事情:
1、 如果不存在到汇点的增广路(即汇点的层数不存在),我们即可停止增广。
2、 确保我们找到的增广路是最短的。
它与最短增广路算法不同之处是:最短增广路每个阶段执行完一次BFS增广后,要重新启动BFS从源点Vs开始寻找另一条增广路;而在Dinic算法中,只需一次DFS过程就可以实现多次增广,这是Dinic算法的巧妙之处。Dinic算法具体步骤如下:
(1)初始化容量网络和网络流。
(2)构造残留网络和层次网络,若汇点不再层次网络中,则算法结束。
(3)在层次网络中用一次DFS过程进行增广,DFS执行完毕,该阶段的增广也执行完毕。
(4)转步骤(2)。
在Dinic的算法步骤中,只有第(3)步与最短增广路相同。在下面实例中,将会发现DFS过程将会使算法的效率有非常大的提高。
构造层次网络就是给图分层,使得增广路最短
1.2.2 复杂度
因为一次DFS的复杂度为 \(O(nm)\) ,所以,Dinic算法的总复杂度即\(O(n^2m)\)。
1.2.3 模板
还是以模板题为例
#include <bits/stdc++.h>
#define LL long long
using namespace std;
int cnt=1;
int n,m,s,t;
int u,v,w;
bool vis[205];
int head[205];
int d[205];
struct node{
int next,to,w;
}e[10005];
LL ans=0;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
void add(int x,int y,int w){
e[++cnt].w=w;
e[cnt].to=y;
e[cnt].next=head[x];
head[x]=cnt;
}
bool bfs(){
memset(d,0x3f,sizeof(d));
memset(vis,0,sizeof(vis));
queue<int>q;
vis[s]=1;
d[s]=0;
q.push(s);
while (!q.empty()){
int top=q.front();
q.pop();
for (int i=head[top];i;i=e[i].next){
if (d[e[i].to]>d[top]+1&&e[i].w){
d[e[i].to]=d[top]+1;
if (!vis[e[i].to]){
vis[e[i].to]=1;
q.push(e[i].to);
}
}
}
}
if (d[t]==d[0]){
return 0;
}
return 1;
}
LL dfs(int x,int minn){
int use=0;
if (x==t){
ans+=minn;
return minn;
}
for (int i=head[x];i;i=e[i].next){
if (e[i].w&&d[e[i].to]==d[x]+1){
int nex=dfs(e[i].to,min(minn-use,e[i].w));
if (nex>0){
use+=nex;
e[i].w-=nex;
e[i^1].w+=nex;
if (use==minn)
break;
}
}
}
return use;
}
int main(){
n=read();m=read();s=read();t=read();
for (int i=1;i<=m;i++){
u=read();v=read();w=read();
add(u,v,w);
add(v,u,0);
}
while (bfs()){
dfs(s,999999999);
}
printf("%lld",ans);
return 0;
}
然后我们就会发现,我们TLE了一个点,这是就需要优化,可以想到至高无上的弧优化。
1.3 Dinic算法+当前弧优化
1.3.1 算法优化
当前弧优化实际上只是增加了一个数组 \(cur\),用 \(cur_i\) 代替邻接表中的 \(head_i\) 。
原理是:当我们在dfs时,从u点出发访问到了第i条边,就说明前i-1条边都已经被榨干了,所以才到了第i条边,因此我们直接改cur[u] = i,下次访问从u点出发的边时,就会直接访问第i条边,省略了前面i-1条边。
不懂的话看看下面代码模板,就会理解了(或者可以去了解一下链式前向星)。
1.3.2 完整代码
#include <bits/stdc++.h>
#define LL long long
using namespace std;
int cnt=1;
int n,m,s,t;
int u,v,w;
bool vis[205];
int head[205];
int d[205];
int cur[205];
struct node{
int next,to,w;
}e[10005];
LL ans=0;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
void add(int x,int y,int w){
e[++cnt].w=w;
e[cnt].to=y;
e[cnt].next=head[x];
head[x]=cnt;
}
bool bfs(){
for (int i=0;i<=n;i++){
d[i]=0x3ffffff;
vis[i]=0;
cur[i]=head[i];
}
queue<int>q;
vis[s]=1;
d[s]=0;
q.push(s);
while (!q.empty()){
int top=q.front();
q.pop();
for (int i=head[top];i;i=e[i].next){
if (d[e[i].to]>d[top]+1&&e[i].w){
d[e[i].to]=d[top]+1;
if (!vis[e[i].to]){
vis[e[i].to]=1;
q.push(e[i].to);
}
}
}
}
if (d[t]==d[0]){
return 0;
}
return 1;
}
LL dfs(int x,int minn){
int use=0;
if (x==t){
ans+=minn;
return minn;
}
for (int i=head[x];i;i=e[i].next){
cur[x]=i;
if (e[i].w&&d[e[i].to]==d[x]+1){
int nex=dfs(e[i].to,min(minn-use,e[i].w));
if (nex>0){
use+=nex;
e[i].w-=nex;
e[i^1].w+=nex;
if (use==minn)
break;
}
}
}
return use;
}
int main(){
n=read();m=read();s=read();t=read();
for (int i=1;i<=m;i++){
u=read();v=read();w=read();
add(u,v,w);
add(v,u,0);
}
while (bfs()){
dfs(s,0x3ffffff);
}
printf("%lld",ans);
return 0;
}
2.求最小割
割\((CUT)\)
割是网络中顶点的划分,它把对于一个网络流图 \(G=(V,E)\)的所有顶点划分成两个集合 \(S\) 和 \(T\),且\(S+T=V\) ,其中源点\(s∈S\),汇点\(t∈T\)。记为\(c(S,T)\)。
定义割\((S,T)\)的容量\(c(S,T)\)表示所有从\(S\)到\(T\)的边的容量之和(注意是有方向的),即\(c(S,T)=\sum\limits_{u\in S, v \in T}c(u,v)\)
就是一个恐怖分子想要,砍断水管使你家断水,至少要砍断那些水管使水管容量和最小
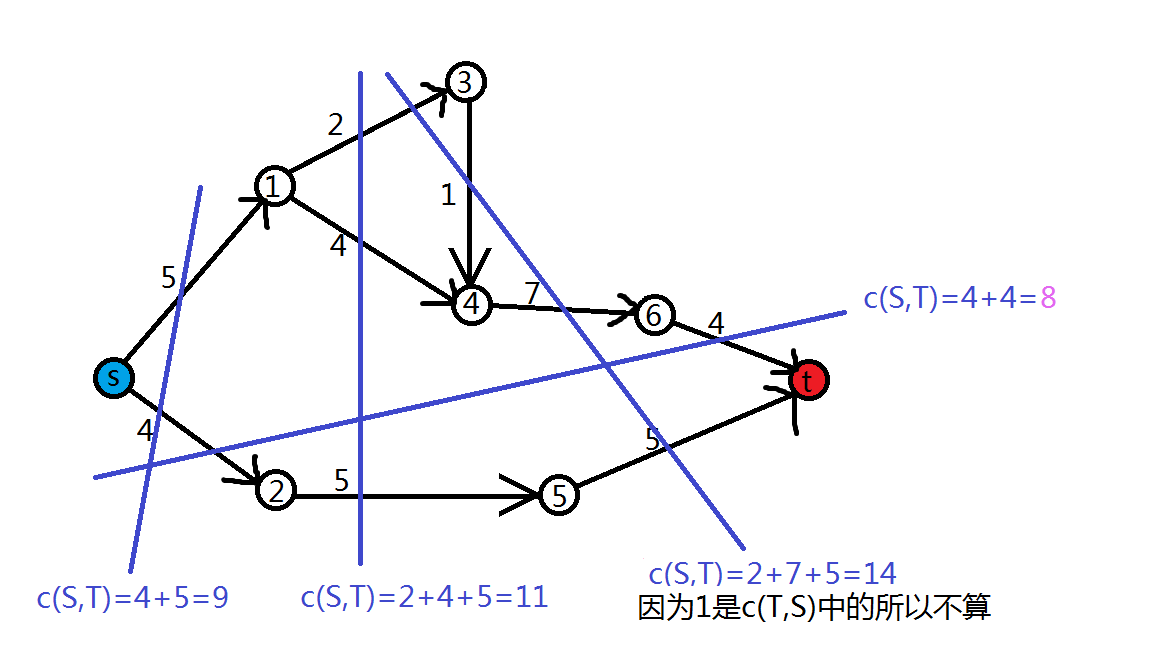
显然上图的最小割是8,但是一想,最大流也是8,这之间有什么关系吗?
2.1 最大流最小割定理
在任何的网络中,最大流的值等于最小割的容量
具体的证明分三部分
1.任意一个流都小于等于任意一个割
这个很好理解 自来水公司随便给你家通点水,构成一个流
恐怖分子随便砍几刀 砍出一个割
由于容量限制,每一根的被砍的水管子流出的水流量都小于管子的容量
每一根被砍的水管的水本来都要到你家的,现在流到外面 加起来得到的流量还是等于原来的流
管子的容量加起来就是割,所以流小于等于割
由于上面的流和割都是任意构造的,所以任意一个流小于任意一个割
2.构造出一个流等于一个割
当达到最大流时,根据增广路定理
残留网络中s到t已经没有通路了,否则还能继续增广
我们把s能到的的点集设为S,不能到的点集为T
构造出一个割集C(S,T),S到T的边必然满流 否则就能继续增广
这些满流边的流量和就是当前的流即最大流
把这些满流边作为割,就构造出了一个和最大流相等的割
相当于在残量网络中,源点能到达的结点的各个边的容量和为最大流
所以如果我们要求一个最小割的边集,我们只要跑一编最大流,然后在残量网络中找正向边残量为0的边,那么这条边肯定在最小割里面,
这样就可以得到一组最小割的边集
3.最大流等于最小割
设相等的流和割分别为F_m和C_m
则因为任意一个流小于等于任意一个割
任意F≤F_m=C_m≤任意C
费用流
介绍
给定一个网络 \(G=(V,E)\),每条边除了有容量限制 \(w(u,v)\) 还有一个单位流量的费用 \(cost(u,v)\)
也就是说在\((u,v)\) 流量为 \(f(u,v)\) 时,需要 \(f(u,v)*cost(u,v)\) 的费用
则该网络中总花费最小的最大流称为 最小费用最大流,即在最大化\(\sum_{(u,v)\in E}f(u,v)\)的前提下最小化\(\sum_{(u,v)\in E}f(u,v)*cost(u,v)\)
SSP算法
SSP(Successive Shortest Path)算法是一个贪心的算法。它的思路是每次寻找单位费用最小的增广路进行增广,直到图上不存在增广路为止。
如果图上存在单位费用为负的圈,SSP 算法正确无法求出该网络的最小费用最大流。此时需要先使用消圈算法消去图上的负圈。(一般用不上)
实现
只需将EK 算法 Dinic 算法中找增广路的过程,替换为用最短路算法寻找单位费用最小的增广路即可。
以模板题P3381 【模板】最小费用最大流为例
#include<bits/stdc++.h>
#define ll long long
#define inf 0x3fffffff
using namespace std;
int u,v,w,c,s,t,n,m;
int head[5005];
bool vis[5005];int cost[5005];
struct node{
int next,to;
int cost,w;
}e[100010];int cnt=1;
void add(int x,int y,int w,int cost){
e[++cnt].cost=cost;
e[cnt].next=head[x];
e[cnt].to=y;
e[cnt].w=w;
head[x]=cnt;
}ll ans=0,anscost=0;
int spfa(){
memset(cost,0x3f,sizeof(cost));
memset(vis,0,sizeof(vis));
queue<int> q;
vis[s]=1;
q.push(s);
cost[s]=0;
while (!q.empty()){
int top=q.front();q.pop();
vis[top]=0;
for (int i=head[top];i;i=e[i].next){
if (cost[top]+e[i].cost<cost[e[i].to]&&e[i].w){
cost[e[i].to]=cost[top]+e[i].cost;
if (!vis[e[i].to]){
vis[e[i].to]=1;
q.push(e[i].to);
}
}
}
}
if (cost[t]==cost[0]) return 0;//cost[0]是一个没有的变量,可以理解为0x3f
else return 1;
}
int dfs(int x,int minn){
int use=0;vis[x]=1;
if (x==t)
return minn;
for (int i=head[x];i;i=e[i].next){
if ((!vis[e[i].to]||e[i].to==t)&&cost[e[i].to]==cost[x]+e[i].cost&&e[i].w){//如果没访问过或者是终点
//且(u的花费+这条路的花费)==v的花费,且这条路的惨量大于0
int nex=dfs(e[i].to,min(minn-use,e[i].w));
if (nex>0){
use+=nex;
anscost+=(nex*e[i].cost);
e[i].w-=nex;
e[i^1].w+=nex;
if (use == minn)break;
}
}
}
return use;
}
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
for (int i=1;i<=m;i++){
scanf("%d%d%d%d",&u,&v,&w,&c);
add(u,v,w,c);
add(v,u,0,-c);
}
while (spfa()){
do{
memset(vis,0,sizeof(vis));
ans+=dfs(s,inf);
}while (vis[t]);
}
printf("%lld %lld\n",ans,anscost);
return 0;
}
后记
之后会出网络流23题(24题 - 1黑题)
让我们敬请期待



 浙公网安备 33010602011771号
浙公网安备 33010602011771号