二分图判断（Java）

二分图定义

设 G = (V, E)是一个无向图，如果顶点V可分割为两个互不相交的子集（A，B），并且图中的每条边（i, j）所关联的两个顶点i, j分别属于这两个不同的顶点集 i in A, j in B,则称图G为一个二分图

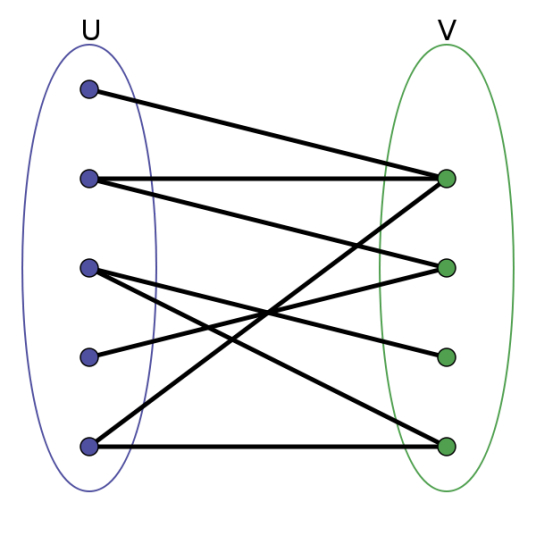
二分图判断

1. 深度优先染色

import java.util.Arrays;

public class BipartiteGraph {
    public boolean isBipartiteGraph(int[][] graph){
        int size = graph.length;

        int []colors = new int[size];   // 结点i的颜色
        Arrays.fill(colors, -1);    // 无色为-1，有色值为0或者1

        for(int i = 0; i < size; i++){
            if (colors[i] == -1){
                // 对没有上色的结点进行上色
                if(!setColorDFS(graph, i, 0, colors)){
                    // 上色失败
                    return false;
                }
            }
        }
        return true;
    }

    private boolean setColorDFS(int[][] graph, int i, int color, int[] colors) {
        if (colors[i] >= 0){
            // 当前结点已经上色
            return color == colors[i];
        }
        colors[i] = color;
        // 对相邻结点进行上色
        for(int neighbor: graph[i]){
            if(!setColorDFS(graph, neighbor, 1 - color, colors)){
                // 上色失败
                return false;
            }
        }
        return true;
    }

    public static void main(String[] args) {
        int[][] graph = {{1,2,3},{0, 2}, {0,1,3},{0,2}};
        BipartiteGraph bg = new BipartiteGraph();
        System.out.println(bg.isBipartiteGraph(graph));
    }
}

2. 广度优先染色

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;

public class BipartiteGraph {
    public boolean isBipartiteGraph(int[][] graph){
        int size = graph.length;

        int []colors = new int[size];   // 结点i的颜色
        Arrays.fill(colors, -1);    // 无色为-1，有色值为0或者1

        for(int i = 0; i < size; i++){
            if (colors[i] == -1){
                // 对没有上色的结点进行上色
                if(!setColorBFS(graph, i, 0, colors)){
                    // 上色失败
                    return false;
                }
            }
        }
        return true;
    }

    private boolean setColorBFS(int[][] graph, int i, int color, int[] colors){
        Queue<Integer> queue = new LinkedList<>();
        queue.add(i);
        colors[i] = color;
        while(!queue.isEmpty()){
            int v = queue.remove();
            for(int neighbor: graph[v]){
                if (colors[neighbor] >= 0){
                    if (colors[v] == colors[neighbor])
                        return false;
                }else{
                    queue.add(neighbor);
                    colors[neighbor] = 1 - colors[v];
                }
            }
        }
        return false;
    }

    public static void main(String[] args) {
        int[][] graph = {{1,2,3},{0, 2}, {0,1,3},{0,2}};
        BipartiteGraph bg = new BipartiteGraph();
        System.out.println(bg.isBipartiteGraph(graph));
    }
}