2025.2.1 - 2.11
Question 1. 「JOISC 2018 Day 4」糖
给定一个长度为 \(N\) 的非负整数序列 \(A\),我们称 \(S\) 是 \(A\) 的独立集仅当 \(S\) 满足如下条件:
- \(S\) 的所有元素在 \([1,N]\) 之间。
- 不存在正整数 \(x\),使得 \(x,x+1\) 都在 \(S\) 中。
- 记 \(V(S)\) 表示 \(S\) 中所有元素 \(x\) 的 \(A_x\) 的和。
已知 \(S\) 的大小最大为 \(K = \Big\lceil{\dfrac{N}{2}}\Big\rceil\),那么对于 \([1,K]\) 内的所有 \(i\) 求 \(|S| = i\) 时 \(V(S)\) 的最大值。
\(N\leq 2\times 10^5, A_i\leq 10^9\)
考虑暴力,有一个很显然的 DP 做法,就是 \(f_{i,j}\) 表示前 \(i\) 个元素中选择了 \(j\) 个时 \(V(S)\) 的最大值,时间复杂度为 \(\mathcal{O}(N^2)\)。
但是这个 DP 做法非常难以优化,我们考虑换一种做法——反悔贪心。
假设选择了 \(A_x\),将 \(A_{x-1}, A_x, A_{x+1}\) 从中剔除,并将 \(A_{x-1} + A_{x+1} - A_x\) 加入到原先 \(x\) 的位置当中。如果接下来选中了这个元素,等价于把 \(A_x\) 从选择中踢出,然后将 \(A_{x-1}, A_{x+1}\) 加入到选择中来,按照这个步骤,每次找出当前的最大值即可,时间复杂度为 \(\mathcal{O}(N^2)\)。
这个做法就有非常大的优化空间,考虑使用 STL 快速维护当前的序列局面即可,时间复杂度降为 \(\mathcal{O}(N\log_2 N)\),可以通过。
Question 2. 「JOISC 2022 Day 3」洒水器
给定一棵 \(N\) 个结点的树,点有初始点权 \(H_i\),边的长度均为 \(1\),有 \(Q\) 个操作,类型如下:
1 x d w,表示将距离结点 \(x\) 不超过 \(d\) 的点的点权乘上 \(w\)。2 x,询问结点 \(x\) 的当前点权,答案对 \(L\) 取余。
\(N\leq 2\times 10^5, Q\leq 4\times 10^5, L\leq 10^9, d\leq 40\)
暴力的复杂度是 \(\mathcal{O}(NQ)\),这里不做讲述。
钦定某个根节点,考虑到 \(d\leq 40\),也就是说,仅考虑向上跳祖先的话,暴力跳并且做 \(\mathcal{O}(1)\) 的操作是可以接受的。
考虑维护 \(T_{u,d}\) 表示对距离结点 \(u\) 的子树中距离是 \(d\) 的点,在结点 \(u\) 上标记的乘法操作总乘积。
如何维护?考虑到每往上跳一次,距离范围额外减一,所以在每个结点 \(u\) 处标记最深的两层结点即可。
举个例子:假设 \(1\) 操作的 \(x=3,d=3\),那么在 \(3\) 号结点处操作 \(T_{3,2}, T_{3,3}\),在 \(3\) 号结点的祖先 \(2\) 号处操作 \(T_{2,0}, T_{2,1}\)。
注意如果当跳到根节点时需要把所有剩余的距离操作完。
对于所有询问,暴力跳 \(\max D\) 级祖先即可,时间复杂度为 \(\mathcal{O}(ND+QD)\)。
Question 3. XOR of N Numbers Equals 0
给定一个正整数 \(N\),求最小的正整数 \(M\),使得可以在 \([1,M]\) 中选择恰好 \(N\) 个不同的正整数,它们的异或为 \(0\)。
如果有解,设 \(M_{\min}\) 表示合法 \(M\) 的最小值,当 \(M_{\min} - N\leq 10^6\) 时,需要构造一组方案,描述没有选择的数字。
\(N\leq 10^{18}\)
Attention is all you need!
接下来将构造性地证明结论是成立的,并将在 \(\mathcal{O}(1)\) 的时间复杂度内求解。
Lemma
设 \(X(n)\) 表示 \(1\sim n\) 内所有数的异或和,则:
此处不再证明。
Use It!
对于 \(N=1\),选不了 \(0\),显然无解;对于 \(N=2\),选不了两个相同的数,只有相同的两个数异或才为 \(0\),显然无解,接下来的讨论仅针对 \(N\ge 3\)。
根据异或的运算定律,选出的数字异或为 \(0\) 等价于没有选择的数字(最终输出)异或与 \(X(M)\) 相等,问题等价于选出一些数字使得异或为 \(X(M)\)。
- 对于 \(N\equiv 3\pmod 4\),根据引理,\(X(N) = 0\),故不需要额外添加数字,所以 \(M_{\min} = N\)。此时所有数字全部选中。
- 对于 \(N\equiv 0\pmod 4\),根据引理,\(X(N)\ne 0\),此时一定需要额外添加数字。当添加一个数字时,\(X(N+1) = 1\),此时不选中 \(1\),故 \(M_{\min} = N+1\)。
- 对于 \(N\equiv 2\pmod 4\),且 \(N+2\) 不是 \(2\) 的幂,根据引理,\(X(N)\ne 0, X(N+1) = 0\),均不能求解(\(N+1\) 不行是因为不能选 \(0\))。考虑 \(X(N+2) = N+2\),将 \((N+1)\oplus (N+2)\) 与 \(N+1\) 标记为未选中。显然 \(N+1\ne N+2\),且 \(N+1,N+2\) 均没有改变 \(N\) 二进制下的最高位(它们的二进制下有共同的最高位),故 \((N+1)\oplus (N+2)\) 的二进制最高位一定比 \(N\) 的最高位小。如果 \(N+2\) 是 \(2\) 的幂,那这样选肯定不行。故此时的 \(M_{\min}= N+2\),不选择的数字为 \((N+1)\oplus (N+2), N+1\)。
- 对于 \(N\equiv 2\pmod 4\),且 \(N+2\) 是 \(2\) 的幂,则无法使用上一个 Case 的讨论结果。考虑 \(X(N+3) = 1\),这里直接将 \(3,N-1,N+1\) 标记为不选中的即可,根据条件,则有 \(N-1 \equiv 1\pmod 4, N+1\equiv 3\pmod 4\),故 \((N-1)\oplus (N+1) = 2\),再 \(2\oplus 3 = 1\) 即可完成。故 \(M_{\min} = N+3\)。
- 对于 \(N\equiv 1\pmod 4\),且 \(N+3\) 不是 \(2\) 的幂,根据引理,\(X(N)\ne 0, X(N+1) = N+2\),均不能求解(\(N+1\) 不行是因为不能选 \(N+2\))。考虑 \(X(N+2) = 0\),而无法选出两个相同的数(选不了两个相同的数,只有相同的两个数异或才为 \(0\)),考虑 \(X(N+3) = N+3\),类比 Case 3,先将 \(1,N+2\) 标记为未选中的,因为 \(N+2\) 一定是奇数,所以 \((N+2)\oplus 1 = N+1\),再将 \((N+3)\oplus (N+1)\) 未选中,同理,因为 \(N+1,N+3\) 均没有改变 \(N\) 二进制下的最高位(它们的二进制下有共同的最高位),\((N+1)\oplus (N+3)\) 的二进制最高位一定比 \(N\) 的最高位小,如果 \(N+3\) 是 \(2\) 的幂,那这样选肯定不行。故 \(M_{\min} = N+3\),未选中的数字为 \(1, (N+1)\oplus (N+3), N+2\)。
- 对于 \(N\equiv 1\pmod 4\),且 \(N+3\) 是 \(2\) 的幂,则无法使用上一个 Case 的讨论结果。考虑 \(X(N+4) = 1\),显然 \(N+2\) 比某个 \(2\) 的幂少 \(1\),这样操作空间很大,再标记 \(N\) 为未选中,此时 \(N\oplus (N+2) = 2\),再根据 \(2\oplus 3 = 1\),所以选出 \(1,2\),因为 \(1\oplus 2 = 3\)。故 \(M_{\min} = N+4\),未选中的数字为 \(1,2,N,N+2\)。
综上所述,\(M_{\min} - N\leq 4\),且构造性完成证明,不需要对 \(N\ge 3\) 的数进行任何特殊判定。
DP打个表照着看就可以
Question 4. [CF1139D] Steps to One
有一个初始为空的序列 \(A\),每次等概率选择一个 \([1,m]\) 内的正整数 \(x\) 并追加到 \(A\) 中,当 \(A\) 中所有元素的 \(\gcd = 1\) 时停止,求 \(A\) 的期望长度。
\(1\leq m\leq 10^5\)
概率期望一出,悬着的心就已经似了
考虑列式计算:
考虑其中 $P(len > j) $ 的部分,依旧列式计算:
代入,得:
直接计算即可,时间复杂度为 \(\mathcal{O}(m)\)。
Question 5. 「JOISC 2021 Day 3」保镖
街道上有 \(N\) 个 VIP 将要逛街,第 \(i\) 个 VIP 与时刻 \(T_i\) 到达位置 \(A_i\) 并以每单位时间 \(1\) 单位长度的速度向位置 \(B_i\) 行走。
现在有 \(Q\) 个保镖可以执行保护任务,第 \(j\) 个保镖于时刻 \(P_j\) 到达位置 \(X_j\),保护任务的定义如下:
- 为了保护一个 VIP,很有必要和 TA 一起逛一会街,同时保护 TA。当然,允许保镖在他们逛街逛到一半时才开始保护,或在他们逛街结束前就停止保护。开始和停止保护的时刻不必为一个整数。
- 特别地,尽管可能有多个 VIP 在同一坐标,保镖也最多只能保护一个 VIP。
- 保镖可以在 JOI 街上以每单位时间最多 \(1\) 单位长度的速度随意走动。在他们停止保护一个 VIP 之后,可以去到另一个地方再开始保护另一个 VIP。如果一个保镖和 VIP \(i\) 一起逛街,那么 VIP 将会对他们一起走过的距离的每单位长度给保镖 \(C_i\) 元小费。这里保证 \(C_i\) 是偶整数。
求对于每个保镖可以达到的最大总小费。
\(N\leq 2800, Q\leq 3\times 10^6, 1\leq T_i,A_i,B_i,C_i,P_j,X_j\leq 10^9\),且 \(C_i\) 是偶整数,时限 \(10\text{s}\)。
考虑在位置-时间图上刻画一个 VIP,从 \((T_i,A_i)\) 连向 \((T_i + |A_i-B_i|, B_i)\),夹坐标轴 \(45^{\circ}\),每 \(\sqrt{2}\) 单位的收益是 \(C_i\) 元。
两条线段的交点可能在 \((X+0.5,Y+0.5)\) 处,这就是为什么 \(C_i\) 保证为偶整数。
刻画一个保镖,就是在上面寻找从 \((t,x)\to (t+1,x+c) (c\in \{-1,0,1\})\) 的路径,并求路径覆盖的线段的收益总和。
考虑到 \(45^{\circ}\) 不是好刻画的条件,且 \(0.5\) 并不方便,将坐标轴进行变换。具体地:令 \(x\) 坐标为时间-位置,\(y\) 坐标为时间+位置。此时,我们就已经将线段转化为横平竖直方向,每覆盖 \(1\) 个单位的收益是 \(\dfrac{C_i}{2}\),以下所称的收益与 \(C_i\),均代指除以 \(2\) 后的,横纵坐标均指变换后的坐标系。
先将横纵坐标分别离散化,并将对应的收益线段标记在网格图的每一条边上,这个网格图的大小是 \(\mathcal{O}(N^2)\) 的,边数也是,所以这一段的时间复杂度是 \(\mathcal{O}(N^2)\) 的。
接下来,变换后的坐标系上,就是找一条左上至右下的路径,使得收益最大化,将所有询问点一并离散化后的网格图上进行 DP,设 \(f_{i,j}\) 表示考虑到 \((X_i,Y_j)\) 的最大收益,时间复杂度为 \(\mathcal{O}((N+Q)^2)\),期望得分 \(22\)。
发现将询问点一并离散化并不优秀,考虑只对线段所得到的所有点离散化形成的网格图做 DP,时间复杂度为 \(\mathcal{O}(N^2)\),可以接受。每一个询问点所能够做的操作本质上只有两种:
- 向下,走到网格图上的某一条横线上,向右走到第一个格点处,然后查 DP 值得到收益总和。
- 向右,走到网格图上的某一条竖线上,向下走到第一个格点处,然后查 DP 值得到收益总和。
这是容易枚举做到的,实现时将坐标丢进线段端点离散化后的数值里面二分查一下排名,然后枚举,时间复杂度为 \(\mathcal{O}(QN)\),期望得分 \(42\)。
假定我们要查询某方向得到的最大收益,设当前位置为 \((X,Y)\),走到 \(y = Y_j\) 后再走到 \((X_i,Y_j)\),显然 \(X\) 在离散化数据中的后继就是 \(X_i\),且 \(y=Y_j\) 上 \((X_{i-1},X_i)\) 段的收益是 \(C\),那么总收益是 \(C(X_i - X) + f_{i,j}\),这是一次函数形式,其中 \(C\) 是斜率,\(f_{i,j}\) 是截距,扫描线套李超线段树即可,两个方向都需要做,时间复杂度为 \(\mathcal{O}(N^2 + (N^2 + Q)\log_2 Q)\),可以通过,期望得分 \(100\)。
Question 6. 「JOISC 2023 Day 4」Bitaro 之旅
一条路上有 \(N\) 个景点,第 \(i\) 个景点的位置是 \(X_i\),有 \(Q\) 个询问,第 \(j\) 个询问 Bitaro 从位置 \(S_j\) 个位置出发,重复执行如下操作直至每一个景点都被游览:
- 选择当前距离 Bitaro 最近的,且 Bitaro 没有游览过的景点(若有多个则选择编号较小的那一个),让 Bitaro 走到那个景点并游览它。
\(N,Q\leq 2\times 10^5, X_i,S_j\leq 10^9, X_i < X_{i+1}\)
首先,暴力怎么做?首先找到其左右景点的编号,一定是 \(L = p, R = p+1\),记录当前位置 \(now\),然后每一次暴力扩展 \(L\) 或 \(R\),直至无法扩展为止,时间复杂度为 \(\mathcal{O}(NQ)\),期望得分 \(15\)。
如果在某一步选择了转向,设转向后的目的地是 \(L\),当前点是 \(P\),另一方向的下一个点是 \(R\),则一定有 \(|P - L|\leq |P - R|\),那么 \(|L - R|\geq 2 | P - L |\),翻了一倍。
故每次二分转向后的目的地即可,注意一些小细节,且如果左端点扩展到 \(0\) 或右端点扩展到 \(N+1\) 则可以停止。
时间复杂度为 \(\mathcal{O}(Q\log_2 N\log_2 V)\),其中 \(V\) 为 \(X_i,S_j\) 的值域取 \(10^9\)。
Question 7. 「JOISC 2016 Day 2」雇佣计划
给定一个长度为 \(N\) 的正整数序列 \(A\),执行如下操作共计 \(M\) 次:
1 x,表示查询序列 \(A\) 中大于等于 \(x\) 的数字构成了多少连续段。2 p v,表示将 \(A_p\) 的值改为 \(v\)。
\(N,M\leq 2\times 10^5, x,v\leq 10^9\)
暴力很简单,此处不做讲述,时间复杂度为 \(\mathcal{O}(NM)\),期望得分 \(10\)。
考虑如何计算连续段?序列上的连续段是一种特殊的连通块,而根据著名结论有:连通块数量=点数-边数(前提是连通块中没有环),连续段可以视作 \(i\) 与 \((i+1)\) 之间的连边,显然无环。
点数怎么求?即求序列中 \(\ge x\) 的数的数量,支持单点修改,一棵权值线段树即可。
边数怎么求?即求序列中相邻两个数都 \(\ge x\) 的位置数量,如果再定义序列 \(B\) 满足 \(B_i = \min(A_i, A_{i+1})\),即求 \(B\) 中 \(\ge x\) 的元素数量,也是支持单点修改,再一棵权值线段树即可。
时间复杂度为 \(\mathcal{O}((N+M)\log_2 V)\),期望得分 \(100\)。
Question 8. 「JOISC 2019 Day 1」考试
给定 \(N\) 个二元组 \((S_i,T_i)\),给出 \(Q\) 个询问 \((X_j,Y_j,Z_j)\),对于每一个询问求出满足如下条件的二元组的数量:
- \(S_i\ge X_j\)
- \(T_i\ge Y_j\)
- \(S_i + T_i \ge Z_j\)
\(N,Q\leq 10^5, 0\leq S_i,T_i,X_j,Y_j,Z_j\leq 10^9\)
首先,暴力是简单做的,时间复杂度为 \(\mathcal{O}(NQ)\),期望得分 \(2\)。
如果 \(X_j + Y_j\ge Z_j\),那么这个就是一个简单的二维数点,相当于 \(Z_j\) 的限制没有了,可以做到 \(\mathcal{O}((N+Q)\log_2 N)\)(有一个子任务满足 \(Z_j = 0\),期望得分 \(20\))。
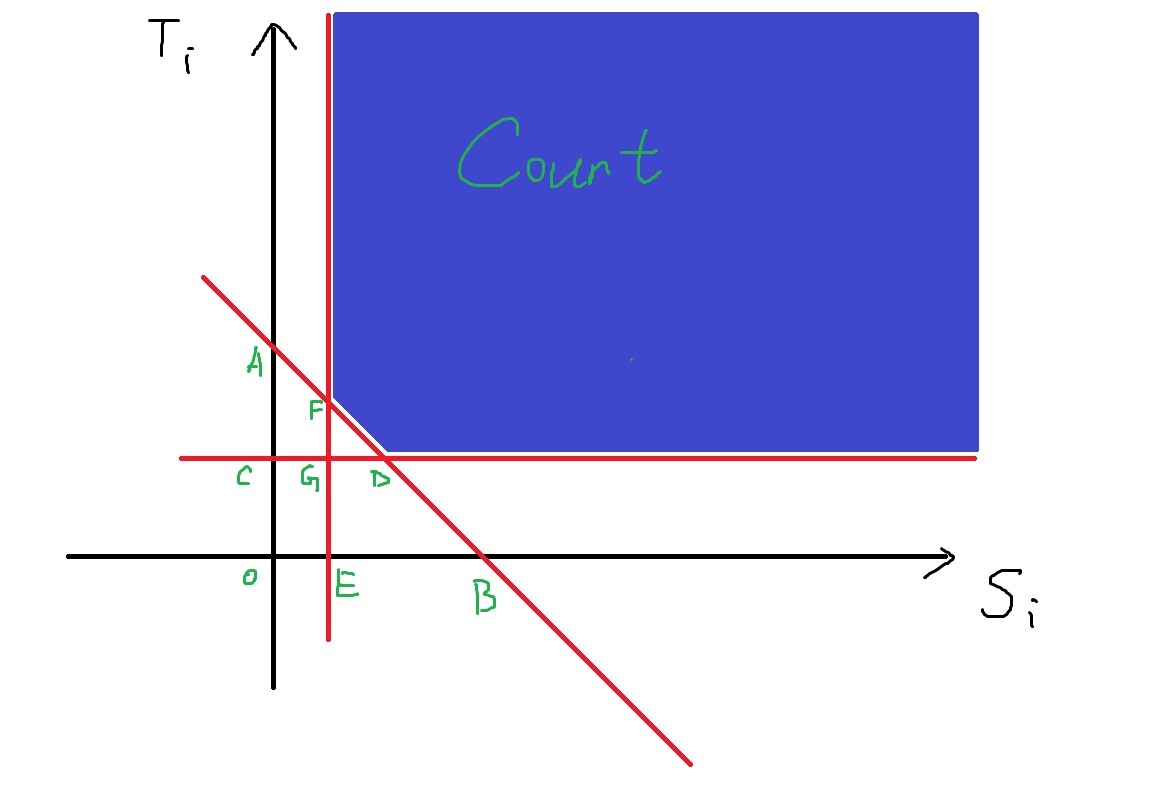
要求蓝色区域,可以用矩形区域减去 \(\triangle DGF\),要求 \(\triangle DGF\),可以用 \(\triangle DGF = \triangle ACD + \triangle BEF + \square OCGE - \triangle OAB\),分别等价于求一下五类点的数量:
- \(S_i\ge X_j, T_i\ge Y_j\),系数为 \(1\)。
- \(S_i\ge X_j, S_i + T_i < Z_j\),系数为 \(-1\)。
- \(T_i\ge Y_j, S_i + T_i < Z_j\),系数为 \(-1\)。
- \(S_i < X_j, T_i < Y_j\),系数为 \(-1\)。
- \(S_i + T_i < Z_j\),系数为 \(1\)。
四个二维数点与一个二分即可,时间复杂度为 \(\mathcal{O}((N+Q)\log_2 N)\),期望得分 \(100\)。
Question 9. 「JOISC 2023 Day1」两种货币
给定一棵大小为 \(N\) 的树,树的边上有 \(M\) 个收费站,第 \(i\) 个收费站在 \(P_i\) 号边上,收费 \(1\) 个金币或者 \(C_i\) 个银币,经过该收费站一次需要交对应的钱。
有 \(Q\) 组询问,每一组询问给定 \(X_j,Y_j,G_j,S_j\),表示询问从 \(X_j\) 走到 \(Y_j\),初始拥有 \(G_j\) 个金币与 \(S_j\) 个银币是否足够?如果足够,最多能够剩下多少金币?
\(N,M,Q\leq 10^5, 1\leq C_i,G_j\leq 10^9, 1\leq S_j\leq 10^{18}\)
问题等价于,如果只用 \(S_j\) 个银币交收费站的钱,最多能够交多少个收费站。
显然的,根据贪心,用银币交的一定是 \(C_i\) 最小的若干个收费站,问题转化为链上前 \(k\) 小的和,如果是全局问题,容易在权值线段树上二分做到,用可持久化权值线段树计算即可。
时间复杂度为 \(\mathcal{O}((N+Q)\log_2 V)\),差不多就这个量级,期望得分 \(100\)。
好久没有写主席树了,有点生疏
Question 10. Point Sets
设 \(S\) 为点集 \(\{(x,y)\mid x,y\in [0,n]\cap \mathbb{N}\}\),求满足 \(T\subseteq S\) 且存在直线 \(l\) 满足 \(l\) 过 \(T\) 中恰好两点的 \(T\) 的数量。
答案对 \(998244353\) 取余。
\(n\leq 10^{11}\)
设 \(m = n+1\)。
首先可以发现,如果 \(T\) 中的点不共线,且 \(|T|\ge 3\),则 \(T\) 恒满足条件,所以可以分为以下几个方面计数:
- 任意选点的方案数,一定为 \(2^{m^2}\)。
- 减去不选点的方案数,一定为 \(1\)。
- 减去只选一个点的方案数,一定为 \(m^2\)。
- 减去选中至少 \(3\) 个点且它们共线的方案数。
而对于第 \(4\) 类,我们又可以将其细分:
- 共水平线。
- 共竖直线。
- 共斜 \(45^{\circ}\) 线。
- 共其它的线。
对于第 \(1,2\) 种:就相当于 \(m\) 个点里至少选 \(3\) 个点,且有 \(2m\) 条线,设 \(f(n) = 2^n - \dbinom{n}{0} - \dbinom{n}{1} - \dbinom{n}{2}\),则总计 \(2mf(m)\) 种。
再记录一点,对于 \(f(n)\),将其写成 \(f(n) = 2^n - 1 - n - \dfrac{n(n+1)}{2}\),则 \(f(0) = f(1) = 0\),这可以方便我们的推导。
对于第 \(3\) 种:每一条斜向上的,可以唯一对应一条斜向下的,通过推导式子:
可得,总计 \(2(2S(m-1)+f(m))\) 种方案。
对于第 \(4\) 种:枚举斜率 \(\dfrac{dy}{dx}\),当 $1\leq dx < dy $ 时,可以对应 \(\dfrac{dx}{dy}\),同时可以对应另两条斜率互为相反数的,所以:
解释以下这个式子的最初形式,枚举斜率 \(\dfrac{y}{x}\),枚举跨过了 \(w\) 个这样的斜率,那么起点一定落在 \(x_0\in [0,n-wx], y_0\in [0,n-wy]\) 中,且终点为 \((x_0 + wx, y_0 + wy)\),对于跨过了 \(w\) 个间隔,起点与终点必选,为了达到 \(3\) 个,中间必须再至少选择一个,故减去一个什么都不选的不合法情况。
另外,推导式子的过程中可能遇到以下情况:
因为 \(\gcd(n,m) = \gcd(n,n-m)\),所以互质的数总是成对出现,且总和为 \(n\),设 \(\epsilon(n) = [n=1]\),则 \(H(n) = \dfrac{n\varphi(n) + \epsilon(n)}{2}\)。
转化到最终形式之后,本质上是 \(\varphi(x), x\varphi(x), x^2\varphi(x)\) 的求和,杜教筛即可,最终 \(C(n)\) 的答案要乘上 \(4\)。
时间复杂度为 \(\mathcal{O}(n^{2/3})\),杜教筛同时算三个值快很多,计算的时候传三元组即可。
Question 11. 「HNOI2009」积木游戏
向第一象限的平面内堆叠矩形,共 \(N\) 次操作,第 \(i\) 次操作堆叠的矩形满足左边界为 \(x = l_i\),右边界为 \(x = r_i\),高度为 \(H_i\),当矩形下底面触碰到地面(\(x\) 轴)或者某个矩形的上底面时该矩形停止下落,定义一个洞为一块连通的没有矩形的面积 $ > 0$ 的空白区域,空白区域内的任意点在不穿过任意矩形(包括矩形间的接触面与接触点)的情况下不能到达无限远处。每堆叠一个矩形后,询问新形成的洞的数量。
\(N\leq 10^6, 0\leq l_i < r_i\leq 10^5, 1\leq H_i\leq 10^3\)
首先,我们来思考以下问题:
Q:如何维护这个矩形的堆叠过程?
A:维护一棵线段树,线段树上每一个位置表示 \(x\in [p,p+1]\) 这一段内的高度,需要维护最大值,同时支持区间覆盖。
令第 \(i\) 列为右边界为 \(x=i+1\) 的宽度为 \(1\) 的矩形区域,则 \(x=l_i\) 至 \(x=r_i\) 中间的列为 \((l_i+1)\) 列至 \(r_i\) 列,以下分别用 \(L_i, R_i\) 列代称(用大小写区分)。
这样就可以维护这个过程了,考虑维护的过程中同时计算,分以下情况:
先给出若干定义:
- 称最后一块堆叠的矩形为 Last。
- 称上下均被限制、左右有一边被限制的取余为“半成洞”。
- 称第 \(L_i\) 列,第 \(R_i\) 列为内边界列。
- 称第 \((L_i - 1)\) 列,第 \((R_i + 1)\) 列为外边界列。
- 称内边界列 \(L_i\) 列于外边界列 \((L_i - 1)\) 列对应,内边界列 \(R_i\) 列于外边界列 \((R_i - 1)\) 列对应。
- 称左边界为 \(x = l_i\),右边界为 \(x = r_i\)。
Case 1: 新的洞的形成仅依赖于 Last 的下边界,且不依赖 Last 的左下、右下端点
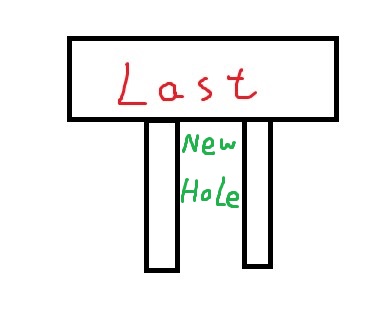
将这个矩形堆叠下去,在 \([L_i,R_i]\) 范围内相邻两个最大值之间会形成一个新的洞,所以需要在线段树上额外维护最大值形成的连续段数量,每一次进行区间查询,设连续段数量为 \(X\),则答案加上 \(X-1\)。
Case 2: 新的洞的形成仅依赖于 Last 的左、右边界,且该洞的下边界不低于 Last 的左下、右下端点
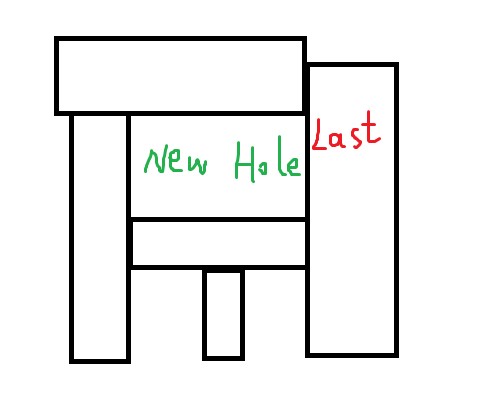
图以左边界为例。
维护每一列在纵向方向上的空白段的上下边界,用这个矩形的上下边界分别去二分空白段的上下边界,具体的,空白段是下边界不低于矩形的下边界,空白段的上边界不高于矩形的上边界,由于纵向增加空白段的坐标是单调递增的,可以使用 vector 与 lower_bound/upper_bound 函数做。
显然的是,新的洞的形成不能同时依赖于 Last 的左右边界,这就意味着它通过下部连通,所以 Last 应该继续掉落。
Case 3: 内边界列没有满
注意两个内边界需要分别考虑。
Case 3.1: 新的洞的形成同时依赖于 Last 的下边界与左、右边界
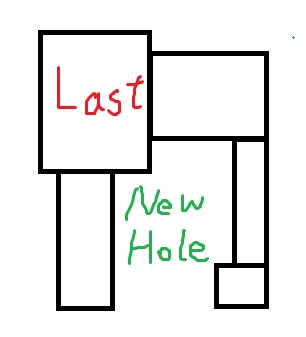
图以右、下边界为例。
根据图,我们可以得知这个新的洞的形成的条件:该内边界列的当前高度不是 \([L_i,R_i]\) 内的最大高度,且矩形的下边界的高度处于对应外边界列的一个半成洞中。
根据线段树求当前高度,再二分是否处于一个半成洞中即可。
Case 3.2: 新的洞的形成仅依赖于 Last 的下边界,但是包括一个矩形的下部端点
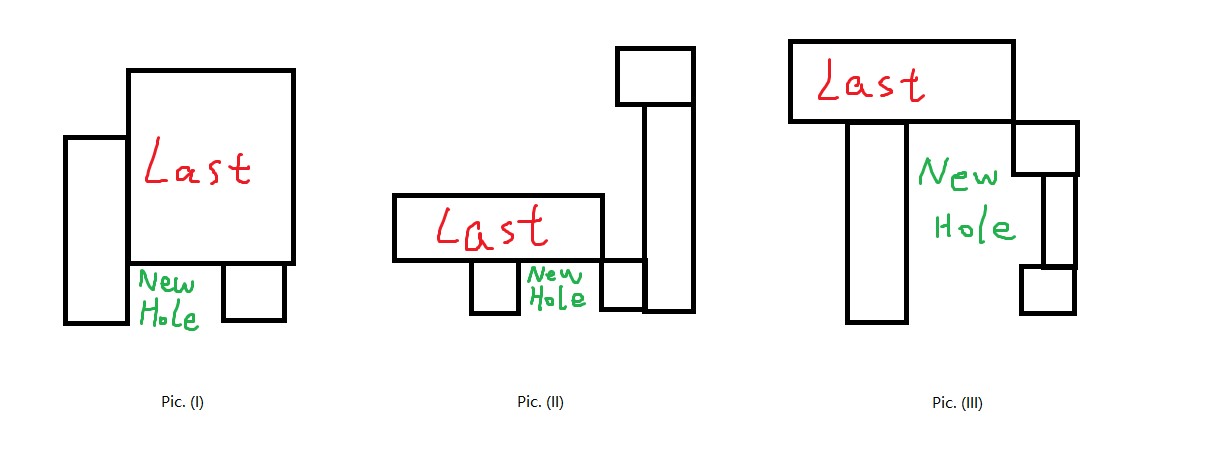
如图(I),外边界列没有半成洞,只要当前矩形的下边界不高于对应的外边界列的当前高度,则额外增加一个新的洞。
如图(II),内边界列的当前高度不是 \([L_i,R_i]\) 内的最大高度,且矩形的下边界的高度不处于对应外边界列的一个半成洞中,则额外增加一个新的洞。
如图(III),外边界列有半成洞,但是矩形的下边界高于外边界列的最高的半成洞的上边界,也只要当前矩形的下边界不高于对应的外边界列的当前高度,则额外增加一个新的洞。
Case 4. 内边界列已满,新的洞的形成只依赖于 Last 的左、右边界,且该洞的下边界低于 Last 的左下、右下端点
注意两个内边界需要分别考虑。
这个情况区分了 Case 2,所以这个新的洞的下边界比 Last 的下边界低。
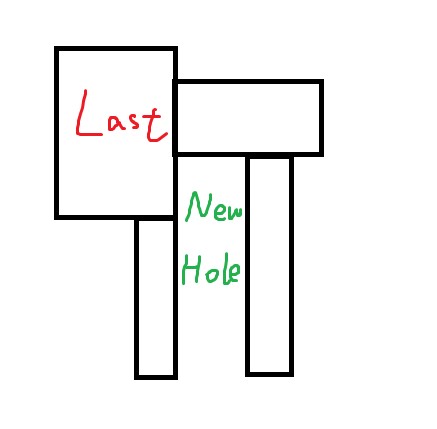
如图,这新的洞的下界比 Last 的下边界低,上界比 Last 的上边界高,且由一个半成洞形成,依旧二分即可。
询问就到这里,修改是容易的,每添加一个矩形,半成洞仅需要考虑第 \(L_i\) 列和第 \(R_i\) 列的即可,感觉一下里面的列之后就用不到了,时间复杂度为 \(\mathcal{O}(N\log_2 N)\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号